Глава 10. Описание токопереноса в полупроводниковых структурах. Макроскопическая система уравнений в линейно полевом приближении.

В гл. 1 были сформулированы уравнения, позволяющие анализировать процессы взаимодействия потока зарядов и электромагнитного поля в вакууме и твердом теле. Прямое использование представленных уравнений затруднительно особенно в случае полупроводниковых приборов, где доминирующее значение имеют физически сложные и многообразные процессы рассеяния. Для достижения практически значимых результатов важно правильно выбрать упрощающие допущения. Этот выбор должен основываться на четком понимании физики происходящих процессов и количественной оценке величин. Основными характеристиками любого физического процесса являются временная и пространственная протяженности. Внешнее воздействие (в нашем случае электромагнитное поле микроволнового диапазона) также характеризуется периодом колебаний и длиной волны . Естественно в таком случае провести анализ характерных пространственных и временных интервалов для основных физических процессов, происходящих в полупроводнике, и провести сравнение их с параметрами воздействующего поля.

1. Временные и пространственные интервалы, характеризующие процесс переноса носителей заряда в полупроводниках.

Движение носителей заряда в полупроводниках происходит в среде, где существуют заряженные ионы и нейтральные атомы. В равновесных условиях любой макроскопический объем квазинейтрален. Поскольку заряды испытывают тепловые флуктуации, то условие нейтральности выполняется в среднем за определенный промежуток времени и в определенном объеме. Похожие свойства имеет газовая плазма. По аналогии с ней в полупроводниках систему заряженных частиц и нейтральных атомов называют плазмой твердого тела. Характерные свойства системы можно определить, возмущая ее внешним воздействием и наблюдая процесс возвращения (релаксации) в стационарное состояние. В качестве такого воздействия могут выступать неоднородный разогрев, инжекция носителей заряда, воздействие электромагнитного поля и т.п. Процесс возвращения в исходное состояние происходит за счет внутренних процессов, присущих рассматриваемой системе (рекомбинация, диссипация энергии в процессах рассеяния и т.п.). Характерные временные масштабы релаксации достаточно полно характеризуют плазму. Учитывая факт перемещения частиц, то или иное возмущение имеет и связанный с временным интервалом – пространственный масштаб локализации возмущения. Рассмотрению этих масштабов и будет посвящен данный параграф.

1. Время релаксации импульса и энергии. Длина свободного пробега, длина «разогрева».

Время релаксации импульса характеризует скорость изменения (уменьшения) импульса при снятии возбуждения. Согласно приближению времени релаксации (1.23) запишем:

или для одномерного случая:

.

Величина имеет смысл среднего времени свободного пробега. Если эту величину умножить на среднеквадратичную тепловую скорость , то получим среднюю длину свободного пробега частицы :

. 101\* MERGEFORMAT (.)

Релаксация энергии частицы происходит с другим характерным временем, т.к. для потери избыточной энергии частице необходимо совершить большое количество актов рассеяния. Это верно для случая упругого рассеяния, которое на практике выполняется ввиду большой разницы в массе взаимодействующих частиц: электронов и ионов (или нейтральных атомов). Перепишем уравнение сохранения энергии (1.24) при снятии внешнего воздействия и без учета пространственной неоднородности потока энергии. В этом случае:

, ,

где - текущая электронная температура, 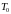- равновесная температура, равная температуре решетки. Тепловые колебания решетки (фононы) являются разновидностью не идеальности кристаллической решетки, на них происходят процессы рассеяния.

Следует заметить, что использование понятия электронная температура правомерно лишь в том случае, когда энергетическое равновесие внутри электронного газа наступает много быстрей чем энергетическое равновесие с решеткой. Это может быть лишь в случае, когда частота межэлектронных столкновений превышает частоту столкновений «электрон-решетка», или . Здесь - характерное время межэлектронных столкновений.

По аналогии с длиной свободного пробега введем в рассмотрение некое расстояние, на котором происходит релаксация энергии. Назовем это расстояние длиной «остывания» - . В случае подачи электрического поля, логичнее назвать эту величину длиной «разогрева». Оценим эту длину следующим образом:

. 202\* MERGEFORMAT (.)

Использование этого понятия важно для анализа особенностей токопереноса в структурах с субмикронными размерами.

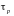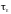Сравним величины и , а также и для случая упругих столкновений (типа электрон-решетка). В этом случае доля передаваемой энергии при одном акте столкновения мала, т.е. 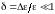. Импульс (скорость) изменяется при таком рассеянии кардинально (прежде всего, по направлению). Частота актов рассеяния равна . Для релаксации энергии требуется большое количество таких актов рассеяния. При этом можно записать: , т.е. . Действительно, в реальных полупроводниковых структурах , а . Иногда говорят, что «память» на импульс у электронов намного короче «памяти» на энергию. Другими словами: процесс релаксации разогретого электронного газа в плазме происходит так, что сначала теряется направленная скорость носителей, а затем происходит выравнивание температуры решетки и носителей. На рис.10.1 графически представлен процесс возвращения функции распределения к равновесному состоянию.

Рис. 10.1. Релаксации функции распределения в равновесное состояние .

Используя выражения 01 и 02 можно заключить, что . При среднеквадратичная скорость составляет . Тогда найдем: , а . Важно отметить, что средняя длина «остывания» находится в пределах одного микрона, что соизмеримо с размерами активных областей современных микроволновых приборов.