Запитання для самоперевірки:

1. Що ви розумієте під поняттям «множина»?

2. Що називається об’єднанням множин?

3. Що називається перерізом множин?

4. Що називається різницею множин?

5. Які числові множини ви знаєте?

Завдання для виконання:

Завдання 1. Дано множину . Перелічити елементи даної множини, якщо:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

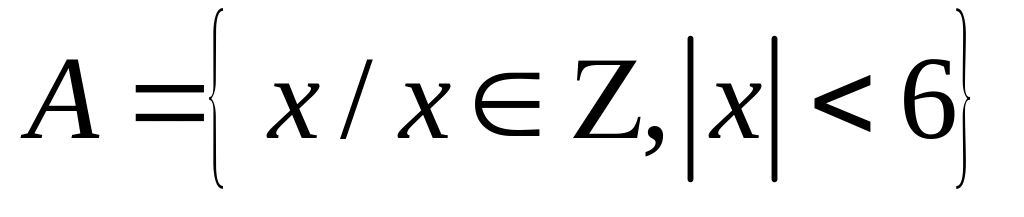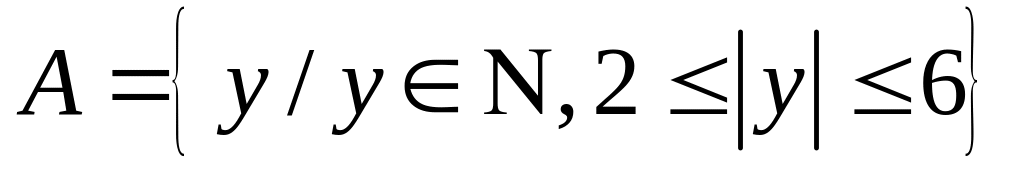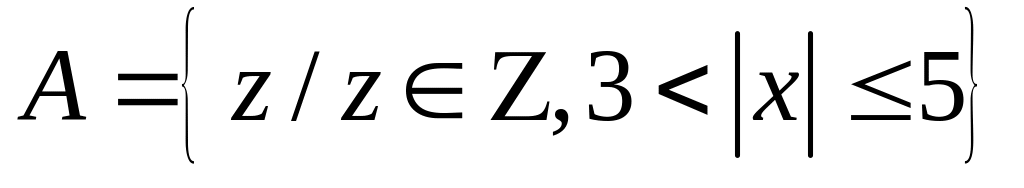Завдання 2. Знайти переріз і об’єднання множин і , якщо:

1. , ;

2. , ;

3. ,

4. , ;

5. , ;

6. ,

7. , ;

8. , ;

9. , ;

10. , .

Завдання 3. Дано множини і . Знайти об’єднання, переріз і різницю цих множин, якщо:

1. , ;

2. , ;

3. , ;

4. , ;

5. , ;

6. , ;

7. , ;

8. , ;

9. , ;

10. , .

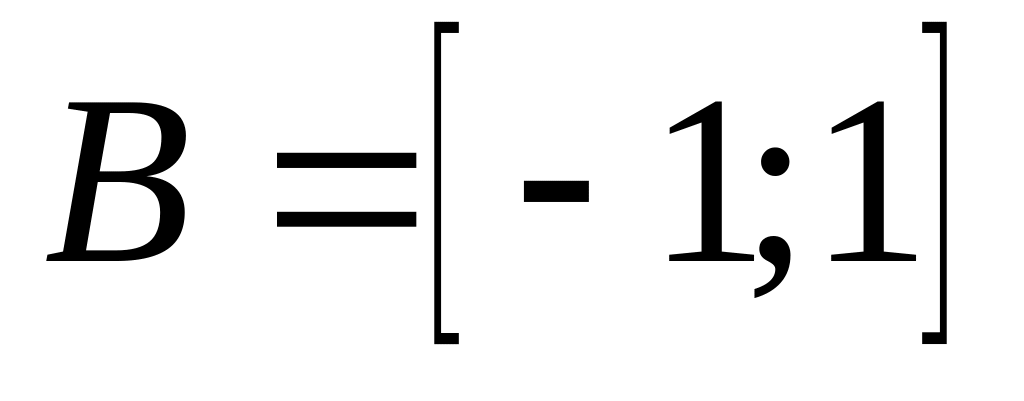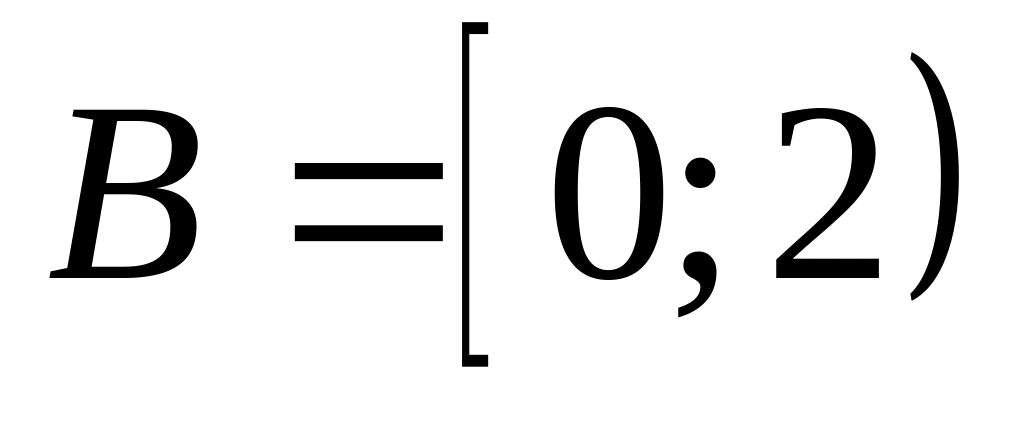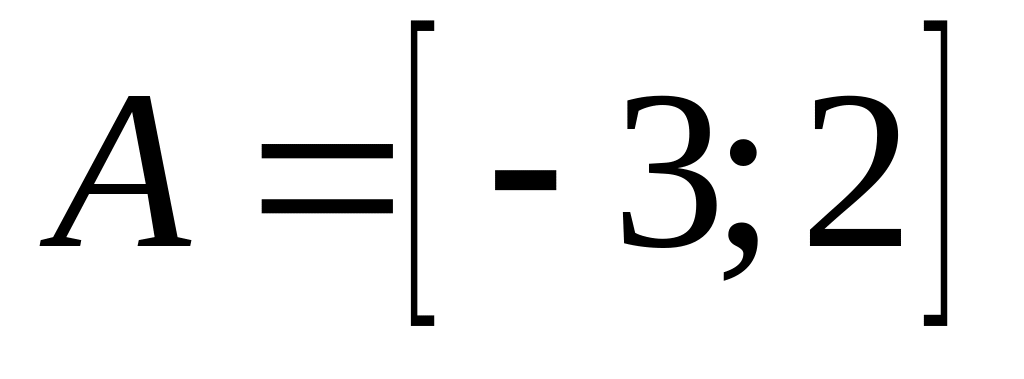Завдання 4. Знайти , , , і зобразити результати на малюнку, якщо:

1. , ;

2. , ;

3. , ;

4. , ;

5. , ;

6. , ;

7. , ;

8. , ;

9. , ;

10. , .

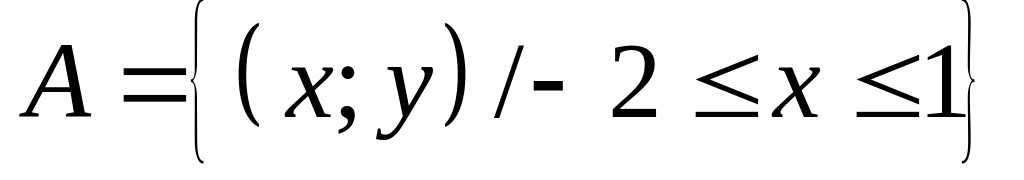Питання 2. Формула складних процентів.

Методичні рекомендації:

1. Означення: Відсотком (процентом) називається одна сота частина

числа 1%= =0,01.

Щоб перетворити число у відсотки, треба помножити дане число на 100.

Щоб перетворити відсотки в число, треба поділити число відсотків на 100.

Основними задачами на відсотки є:

1. Знаходження відсотків від числа.

Щоб знайти відсотки від числа, треба відсотки записати у вигляді дробу і помножити даний дріб на число.

2. Знаходження числа за відомими відсотками.

Щоб знайти число за відсотком, треба відсоток записати у вигляді дробу і поділити число на дріб.

3. Знаходження відсоткового відношення двох чисел.

Щоб знайти відсоткове відношення двох чисел, треба знайти їх частку і записати її у вигляді відсотка.

Означення: Відношення даного відсотка певного числа до самого цього числа називається відсотковою ставкою і позначається р.

Означення: Питомою відсотковою ставкою (нормою відсотка) називається відношення

Під простими відсотками ми розуміємо випадок – коли сума, що накопичується за рік вилучається і нарахування ведеться з початкової суми.

Нехай К- початкова сума (капітал), і - питома відсоткова ставка, п - кількість років. Сума, яку буде накопичено з урахуванням простих відсотків за п років:

(1)

Якщо складний відсоток нараховується протягом п років, виконується рівність:

(2)

Вираз 1+і=r називається коефіцієнтом складного відсотка. Тоді

. (2.1)

Нехай К - кредит, що його банк надає на п років, а - щорічний внесок на погашення боргу наприкінці року. Тоді формула

. (3)

визначає розмір внеску R такого, щоб при взятому кредиті К його було погашено за п років. Вираз

називають коефіцієнтом погашення.

Дисконтуванням називають відшукання початкової суми на підставі її кінцевого значення. Різниця D між кінцевою сумою К_п, яка підлягає дисконтуванню, і дисконтованою сумою К називається дисконтом. Отже,

, (4)

Якщо кошти К надаються під прості відсотки на п років за умови, що питома відсоткова ставка і, тоді дисконтована сума К для К_п визначатиметься формулою

, (5)

Для випадку складних відсотків маємо , (5.1)

Коефіцієнт називається коефіцієнтом дисконту.