Запитання для самоперевірки:

1. Які теореми носять назву «теореми про середнє»?

2. Сформулюйте теорему Ферма, Лагранжа, Ролля, Коші.

3. Яка загальна схема дослідження і побудови графіка функції?

Завдання для виконання:

Завдання 3. Дослідити задану функцію і побудувати її графік.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

Питання 3. Невизначений і визначений інтеграл.

Методичні рекомендації:

Невизначений інтеграл і його властивості.

Нехай задано функцію f, визначену на скінченному або нескінченному проміжку, і треба знайти функцію F, похідна від якої у будь-якій точці дорівнює f : для всіх або .

Означення: Функція , визначена на , похідна від якої на цьому проміжку дорівнює даній функції , називається первісною для функції або для диференціала .

Зрозуміло, що функція теж буде первісною для функції на :

Теорема: Якщо функція є якою-небудь первісною для функції на , то множина всіх первісних для функції на цьому проміжку міститься у формулі .

Якщо - первісна для на і , то вираз називається невизначеним інтегралом функції і позначається символом

Функція називається підінтегральною функцією, вираз називається підінтегральним виразом, а знак ∫ називається інтегралом, тобто

З геометричної точки зору, невизначений інтеграл є множиною кривих, кожна з яких називається інтегральною кривою і утворюється зсувом (паралельним перенесенням) однієї з них паралельно самій собі уздовж осі .

Властивості невизначеного інтеграла :

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції: .

2. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:

3. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:

4. Сталий множник можна виносити за знак інтеграла: .

5. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі цих інтегралів від цих функцій: .

Властивість № 5 справедлива для довільного, скінченного числа доданків.

Основні методи інтегрування.

1. Метод безпосереднього інтегрування.

Означення: Обчислення інтегралів за допомогою основних властивостей невизначеного інтеграла, таблиці інтегралів, називається безпосереднім інтегруванням.

Приклад 1: .

2. Метод підстановки (заміна змінної).

Теорема. Якщо - перервна функція на проміжку , тобто , , і нехай функція визначена і диференційована на проміжку , причому множина значень цієї функції є проміжок . Тоді справедлива формула:

(1)

Приклад 2:

.

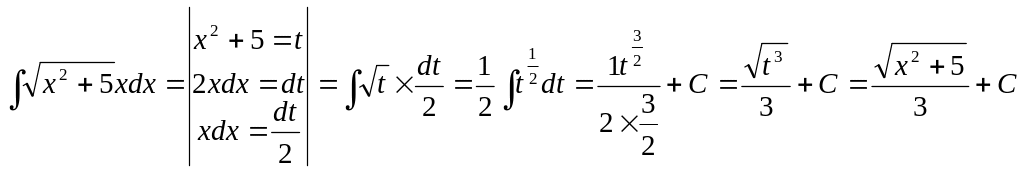3. Метод інтегрування частинами.

Нехай - функції, що мають на деякому проміжку неперервні похідні. Тоді . Інтегруючи обидві частини останньої рівності, дістанемо або

, (2).

Дана формула (2) називається формулою інтегрування частинами. Вона дає змогу звести обчислення інтеграла до обчислення інтеграла .

Приклад 3: .

Таблиця невизначених інтегралів:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. 

15. 

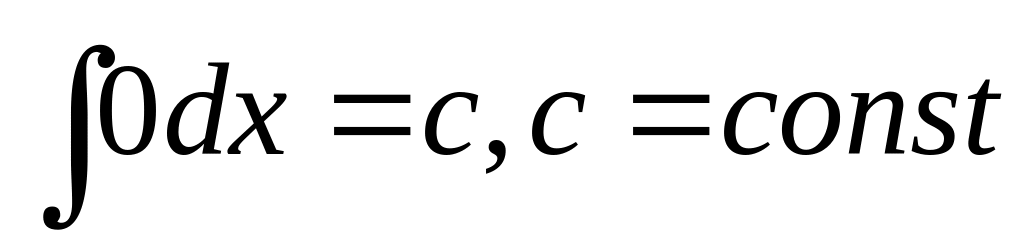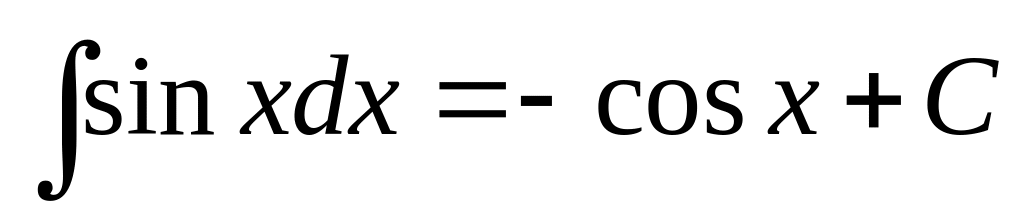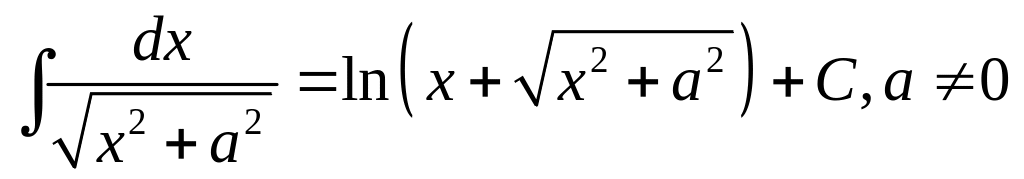
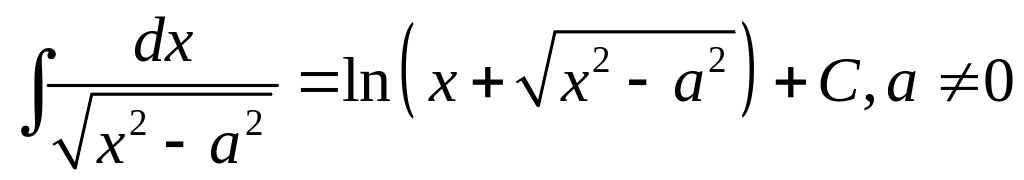
Правила інтегрування раціональних функцій:

Кожна раціональна функція, тобто функція виду , де і – многочлени ( ), має (на кожному проміжку, що не містить коренів ) первісну, яка є елементарною функцією. Розглянемо знаходження невизначеного інтеграла функції , якщо відомо розклад на множники першого та другого степенів.

Означення: Раціональний дріб називається правильним, якщо найвищий показник степеня чисельника менше відповідного степеня знаменника. Дріб називається неправильним, якщо .

Якщо дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержати заданий дріб у вигляді суми многочлена та правильного раціонального дробу, тобто . Найпростішими раціональними дробами називають правильні дроби вигляду:

1. ;

2. ;

3. ;

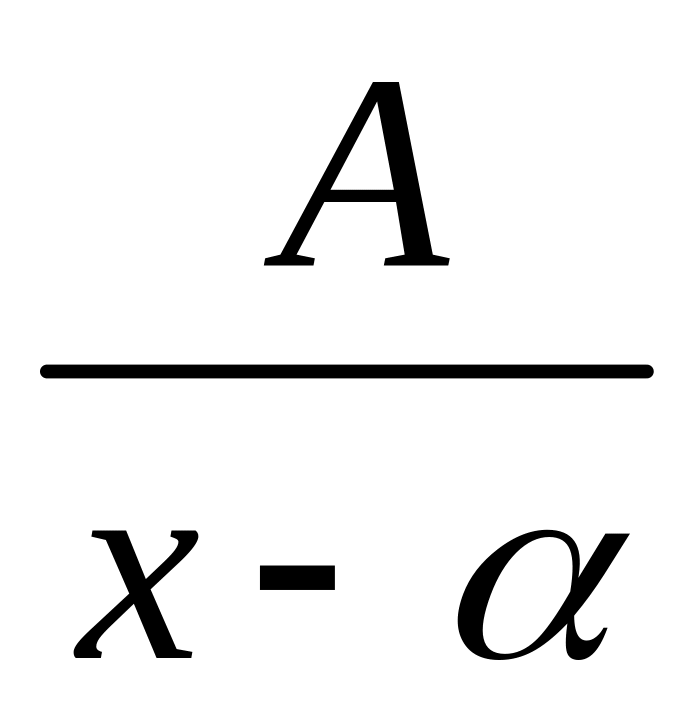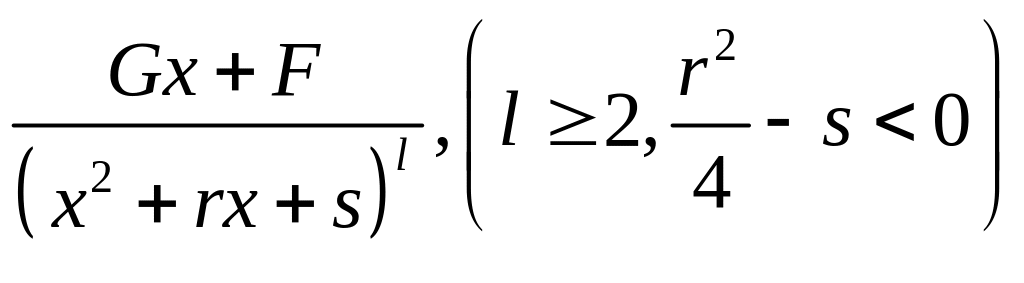4. , – ціле число.

Умова означає, що квадратний тричлен не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен .

Розглянемо інтегрування найпростіших раціональних дробів. Інтеграли від найпростіших раціональних дробів І-го та ІІ-го типів знаходять методом безпосереднього інтегрування:

1. ;

2. ;

3. .

Для інтегрування найпростішого дробу ІІІ типу треба спочатку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну.

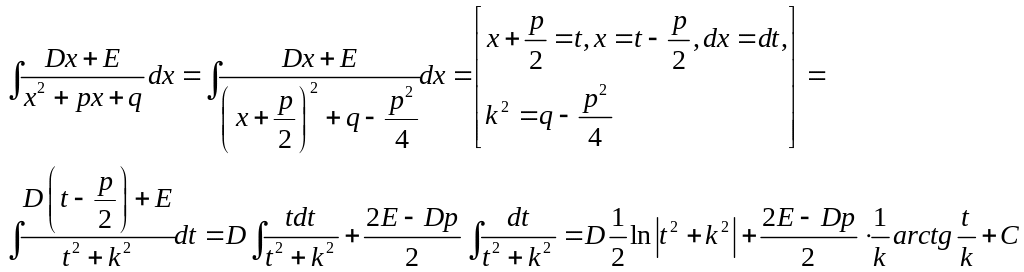
Повертаючись до змінної , та враховуючи, що або , одержимо:

Інтеграл від найпростішого дробу типу ІV шляхом повторного інтегрування частинами зводять до інтеграла від найпростішого дробу типу ІІІ. У повному курсі вищої алгебри доведена наступна теорема:

Теорема: Будь-який правильний раціональний дріб розкладається на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів.

Можливі слідуючі випадки:

1. Корені знаменника дійсні та різні, тобто .

В цьому випадку дріб розкладається на суму найпростіших дробів І типу: (3).

Невизначені коефіцієнти знаходять з тотожності (3).

2. Корені знаменника дійсні, причому деякі з них кратні, тобто

.Тоді дріб розкладається на суму найпростіших дробів І – го та ІІ – го типів:

, (4).

Коефіцієнти знаходять з тотожності (4).

3. Корені знаменника дійсні, причому деякі з них кратні, крім того знаменник містить квадратний тричлен, який не розкладається на множники, тобто . В цьому випадку дріб розкладається на суму найпростіших дробів І –го, ІІ –го та ІІІ –го типів: , де коефіцієнти знаходять з останньої рівності.

Визначений інтеграл як границя інтегральних сум.

Нехай - неперервна на функція. Позначимо через - будь-який набір точок з , що . Набір Т – розбиття на частин.

Розглянемо – довжина . Для кожного визначимо числа – найменше і найбільше значення функції на : , .

Означення. Нижньою сумою Дарбу для функції і набору точок Т на називається сума :

.

Означення: Верхньою сумою Дарбу для функції і набору точок Т на називається сума

.

Очевидно, що

Геометрична інтерпретація:

Якщо на кожному з проміжків вибрати точку : і знайти суму добутків , то позначивши , цю суму називають інтегральною сумою для функції і розбиття Т.

Геометрична інтерпретація:

Зрозуміло, що .

Суми Дарбу – нижня і верхня інтегральні суми.

Означення. Якщо існує єдине число І таке, що для будь-якого набору справджується рівність , то число І називається визначеним інтегралом від функції на :

, - межі інтегрування.

Геометричний зміст визначеного інтеграла:

Інтеграл дорівнює площі криволінійної трапеції, яка обмежена віссю , прямими , і графіком функції :

Умови інтегрованості функції.

Теорема 1. (необхідна умова). Якщо функція неперервна на , то вона інтегрована на цьому відрізку.

Теорема 2. (достатня умова). Якщо функція неперервна на , то вона інтегрована на цьому відрізку.

Теорема 3. Якщо функція обмежена на і неперервна в ньому скрізь, крім скінченого числа точок, то вона інтегрована на цьому відрізку.

3. Теорема: Якщо функція є якою-небудь первісною для неперервної функції , , то справедлива формула:

, (5)

(5) – формула Ньютона-Лейбніца.