Методичні рекомендації:

Основні теореми диференціального числення:

Теорема Ферма: Нехай функція f(х) неперервна на інтервалі і набуває свого найбільшого або найменшого значення у деякій точці с цього інтервалу. Тоді, якщо в точці с існує похідна то .

Геометричний зміст теореми Ферма зрозумілий з малюнка: якщо в точці функція досягла найбільшого чи найменшого значення, то дотична до графіка цієї функції в точці паралельна осі .

Теорема Ролля: Якщо функція f(х) неперервна на відрізку , диференційована в інтервалі і на кінцях відрізка набуває однакових значень , то знайдеться хоча б одна точка , в якій .

Геометричний зміст теореми Ролля: якщо функція задовольняє умови теореми Ролля, то на графіку цієї функції знайдеться хоча б одна точка, в якій дотична паралельна осі .

Теорема Коші: Якщо функції і неперервні на відрізку , диференційовні в інтервалі , причому , то існує така точка , що

.

Теорема Лагранжа: Якщо функція , неперервна на відрізку , диференційовна в інтервалі , то всередині цього інтервалу знайдеться хоча б одна точка , в якій .

Розглянемо геометричний зміст теореми Лагранжа:

Якщо функція задовольняє умови теореми Лагранжа, то на графіку цієї функції знайдеться хоча б одна точка, в якій дотична до графіка паралельна хорді, що сполучає кінці кривої і . Таких точок може бути і кілька, але хоча б одна завжди існує.

Дані теореми мають безпосереднє застосування під час дослідження і побудови графіків функцій.

Загальна схема дослідження функції

1. Знаходження області визначення функції . Встановлення точок розриву і проміжків неперервності функції.

2. Знаходження координат точок перетину графіка з координатними осями: а) з віссю : з рівняння знаходимо ; б) з віссю : знаходимо .

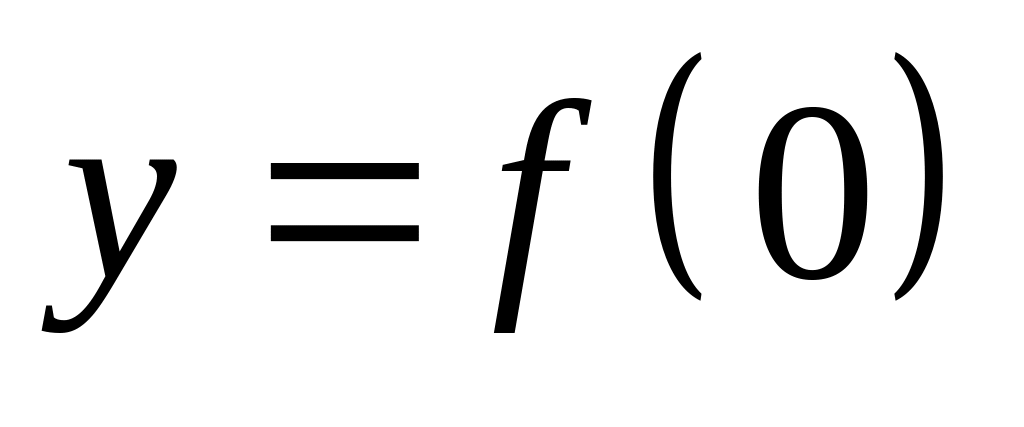3. Дослідження функції:

а) на періодичність: – періодична, якщо , – період ),

б) парність і непарність ( –парна, якщо – симетрична відносно початку координат і та непарна, якщо – симетрична відносно початку координат і ).

4. Асимптоти графіка: вертикальні асимптоти – у точках розриву 2-го роду функції ; похилі асимптоти: , де .

5. Знаходження: а) точок, підозрілих на екстремум: знаходження похідної та критичних точок функції: розв’язування рівняння ;

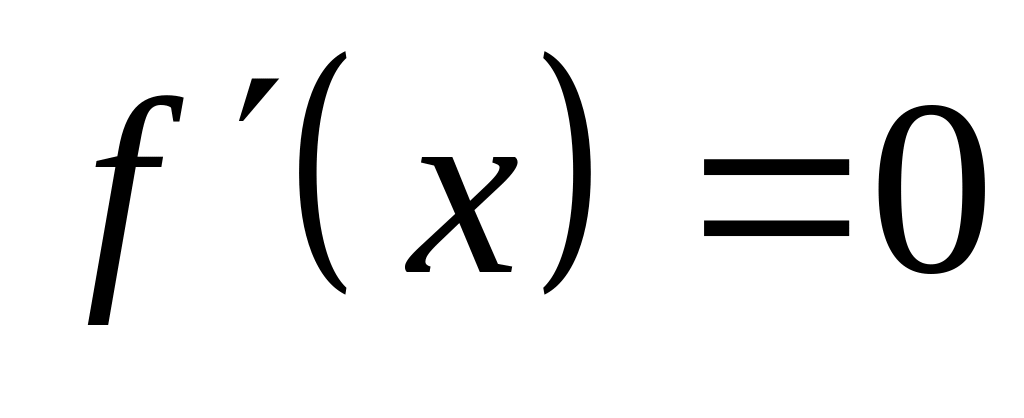б) проміжків монотонності: якщо , то функція зростає, якщо – спадає;

в) точок екстремуму: якщо змінює знак при переході через точку з «+» на «-», то – точка максимуму, в протилежному випадку (з «-» на «+») точка мінімуму.

6. Знаходження: а) другої похідної та критичних точок другого роду: ;

б) інтервалів опуклості і вгнутості: – функція угнута, – функція опукла;

в) точок перегину і значень функції в цих точках: якщо змінює знак при переході через точку , то дана точка є точкою перегину.

7. Побудова графіка функції.

Приклад: Дослідити функцію та побудувати її графік.

Розв’язання:

1. ;

2. При і навпаки.

3. Функція неперіодична.

4. Перевіримо на парність: . Функція непарна.

4. Похилою асимптотою є пряма .

5. . Критичними точками на множині будуть точки . Складемо таблицю:

х	0		1
	0	+	не існує	-	0	+
	0		не існує

6. , при

	0		1
	0	-	не існує	+
	0		не існує

7. Графік функції