Методичні рекомендації:

Для того, щоб навчитись розв’язувати задачі лінійного програмування графічним способом, нагадаємо, як розв’язуються лінійні нерівності з двома змінними.

Означення: Нерівність виду або називається лінійною нерівністю з двома змінними величинами і ( – дійсні числа ).

Точки ( ),які задовольняють рівняння лежать на прямій, яка ділить площину на дві півплощини.

Означення: Множина точок площини, які лежать по один бік від прямої і не лежать на цій прямій називається відкритою півплощиною.

Означення: Множина точок площини, які лежать по один бік ввід прямої разом з точками цієї прямої називається замкненою півплощиною

Теорема: Усі точки однієї з двох відкритих півплощин, на які пряма поділяє площину задовольняють нерівність , а всі точки іншої відкритої півплощини нерівність .

Означення: Система нерівностей виду

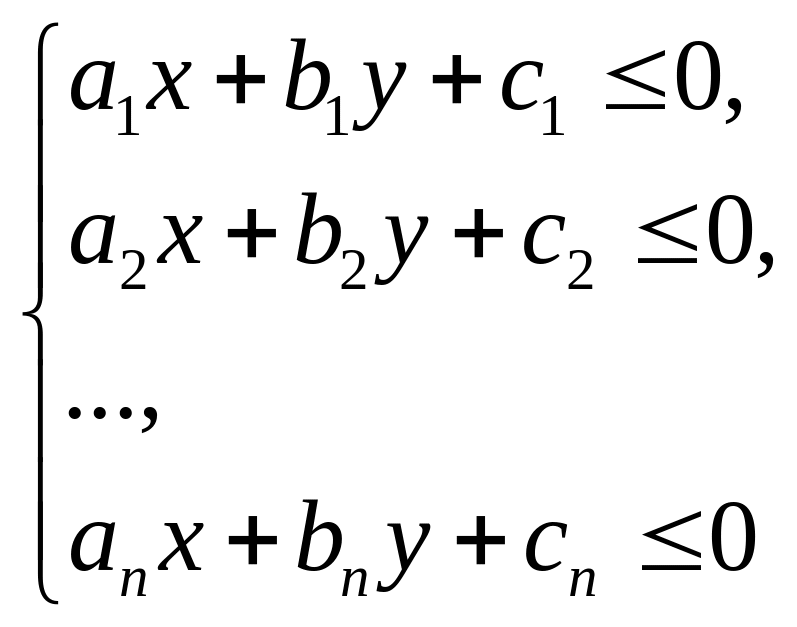(1)

де – дійсні числа, називається системою нерівностей з двома змінними.

Система (1) називається сумісною (несуперечливою), якщо існує хоча б одна точка для якої виконуються всі нерівності системи.

Кожна з нерівностей системи (1) виконується лише для точок із замкненої півплощини, на які ділить півплощину пряма .

Означення: Непустий перетин деякої кількості замкнутих півплощин називається замкненим многокутником.

Означення: Непустий перетин деякої кількості відкритих півплощин називається відкритим многокутником.

Користуючись цими означеннями, основний результат про розв’язування системи нерівностей можна сформулювати так:

Розв’язком сумісної системи нерівностей (1), тобто множиною всіх точок , для яких виконуються всі нерівності системи є замкнений многокутник. І навпаки кожний замкнений многокутник є розв’язком системи нерівностей типу (1)

Означення: Вираз (2), де – дійсні числа, – змінні, називається лінійною функцією двох змінних .

Якщо , то матимемо рівняння прямої (3

Прямі лінії на площині , паралельні прямій, що визначається рівнянням (3), називають лініями рівнів лінійної функції (2).

Властивості лінійної функції двох змінних:

1. В усіх точках кожної з прямих функція зберігає стале значення, а при переході до іншої прямої її значення змінюється.

2. Функція зростає у напрямі, що визначається вектором прямої .

3. Вектор показує напрям зменшення значень функції.

4. На будь-якому відрізку функція (2) досягає найбільшого (найменшого) значення на одному з кінців відрізка.

Розглянемо лінійну функцію двох змінних . Для кожної пари чисел лінійна функція набуває певного значення , яке називатимемо значенням лінійної функції в точці і позначатимемо .

Теорема: Лінійна функція , що розглядається в точках довільного трикутника, набуває свого найбільшого та найменшого значень у певній вершині цього трикутника.

Означення: Множина точок площини називається опуклою, якщо разом з кожними її двома точками А і В вона містить весь відрізок, що сполучає ці точки.

Множина, яка містить одну точку або порожня множина вважаються опуклими.

Теорема: Лінійна функція , що розглядається в точках опуклого многокутника, набуває свого найбільшого (найменшого) значення в якійсь вершині цього многокутника.

Користуючись цією теоремою можна знайти найбільше (найменше) значення функції на деякому многокутнику, який одержимо з системи обмежень. Адже ми знаємо, що в загальному випадку задача лінійного програмування має вигляд:

,

– деякі числа, – змінні.

Отже, графічний спосіб розв’язування задач лінійного програмування полягає в

1. побудові многокутника Ω;

2. побудові вектора ;

3. підстановці в функцію крайніх (по напряму вектора) точок – вершин многокутника.

Недоліки графічного способу:

1) його застосовують лише у випадку двох змінних;

2) громіздкість.