
- •Задание № 1.
- •Пример решения задачи из задания № 1
- •Задание № 2.
- •Пример решения задачи из задания № 2.
- •Задание № 3.
- •Пример решения задачи из задания № 3.
- •Задание № 4.
- •Пример решения задачи из задания № 4.
- •Задание № 7.
- •Пример решения задачи из задания № 7.
- •Задание № 8.
- •Пример решения задачи из задания № 8.
- •Задание № 9.
- •Пример решения задачи из задания № 9.
- •Задание № 10.
- •Пример решения задачи из задания №10.
- •Рекомендуемая литература
Задание № 10.
Найти область сходимости функционального ряда.
1.
 . 2.
. 2.
 .
.
3.
 .
4.
.
4.
 .
.
5.
 . 6.
. 6.
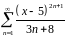 .
.
7.
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Пример решения задачи из задания №10.
Для
решения задач этого раздела можно
использовать признаки сходимости
Даламбера или Коши. Если для числового
ряда
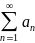
вычислить
 ,
,
то
в случае если
 то ряд сходиться абсолютно, если
то ряд сходиться абсолютно, если
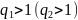 ,
то ряд будет расходящимся. Если
,
то ряд будет расходящимся. Если
 требуется дополнительное исследование.
требуется дополнительное исследование.
Для
функциональных рядов мы будем использовать
признак Вейерштрасса, т.е. сами члены
функционального ряда

мажорируются членами знакоположительного сходящегося числового ряда
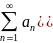 то
функциональный ряд сходится равномерно
в своей области определения.
то
функциональный ряд сходится равномерно
в своей области определения.
Рассмотрим пример: пусть имеется функциональный ряд

Найдем предел дроби



По
признаку Даламбера если
 , то ряд будет сходящимся. Таким образом
область сходимости ряда включает
интервал (0,2). Проведем дополнительное
исследование для случая, когда x=0
или x=2,
т.е.
, то ряд будет сходящимся. Таким образом
область сходимости ряда включает
интервал (0,2). Проведем дополнительное
исследование для случая, когда x=0
или x=2,
т.е.
 .
.
В этих случаях получаем числовой ряд

Этот ряд, очевидно, расходится, т.к. не выполняется необходимый признак сходимости
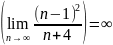
Поэтому
окончательный ответ - исходный ряд
сходится для
 .
.
Рекомендуемая литература
. Шипачев В.С. Высшая математика. - М.: Высшая школа, 1985.
Пискунов Н.С. Дифференциальное и интегральное исчисление для Втузов. - М.: Наука, 1985, т. 1,2.
Письменный Д.Т. Конспект лекций по высшей математике. – М: Айрис-пресс,2005.
Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. - М.: Наука, 1984.
Ефимов А.В., Демидович Б.П. Сборник задач по математике для Втузов. Линейная алгебра и основы математического анализа. - М.: Наука, 1981.
Кремер Н.Ш. Практикум по высшей математике для экономистов.- М: ,ЮНИТИ, 2005.
Берман Г.Н. Сборник задач по курсу математического анализа.- М: Санкт-Петербург, 2005.
Красс М.С., Чупрынов Б.П. Математика для экономистов. – М: Санкт-Петербург,2005.
Фихтенгольц Г.М. "Курс дифференциального и интегрального исчисления", - М.: Лань, 1977 г.
Примерный перечень вопросов к экзамену по математическому анализу.
Абсолютная величина числа, ее свойства.
Понятие функции, общие свойства, график функции.
Предел функции в точке и на бесконечности.
Бесконечно малая и бесконечно большая, их свойства.
Основные теоремы о пределах.
Первый замечательный предел.
Последовательность, предел последовательности. Теорема Вейерштрасса (о пределе монотонной ограниченной последовательности).
Второй замечательный предел. Число e, натуральные логарифмы.
Непрерывность функции. Свойства непрерывных функций.
Производная. Геометрический и механический смысл производной.
Производная суммы, произведения, частного, сложной функции.
Таблица производных (вычисление производных элементарных функций).
Дифференциал функции, его свойства.
Производные и дифференциалы высших порядков.
Теоремы Ферма и Ролля.
Теоремы Лагранжа и Коши.
Теоремы монотонности функций.
Экстремум функции. Необходимое и достаточное условие экстремума.
Выпуклость и вогнутость функций. Точки перегиба.
Асимптоты функций.
Общая схема исследования функций.
Правило Лопиталя.
Формула Тейлора. Остаточный член в форме Лагранжа.
Формула Тейлора для функции многих переменных.
Производная по направлению, градиент.
Метод наименьших квадратов.
Первообразная. Неопределенный интеграл, его свойства.
Методы интегрирования.
Интегрирование рациональных дробей.
Интегрирование тригонометрических выражений.
Определенный интеграл, его свойства.
Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Замена переменных в определенном интеграле. Интегрирование по частям в определенном интеграле.
Несобственные интегралы.
Приближенное вычисление интегралов.
Приложения определенного интеграла.
Дифференциальные уравнения, общие свойства.
Уравнения с разделяющимися переменными. Однородные и приводящие к ним дифференциальные уравнения.
Линейные дифференциальные уравнения 1-го порядка.
Линейное однородное дифференциальное уравнение второго порядка с постоянным коэффициентом.
Линейное неоднородное дифференциальное уравнение второго порядка с постоянным коэффициентом.
Метод вариации произвольных постоянных.
Ряды. Общие свойства. Достаточный признак сходимости.
Знакоположительные ряды. Признак сравнения.
Признаки Даламбера и Коши.
Интегральный признак сходимости ряда.
Знакопеременные ряды. Теорема Лейбница.
Функциональные ряды. Общие свойства.
Степенные ряды. Теорема Абеля. Радиус сходимости.
Свойства степенных рядов.
Ряды Тейлора и Маклорена.
Разложение некоторых элементарных функций в степенные ряды.
