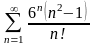- •Задание № 1.
- •Пример решения задачи из задания № 1
- •Задание № 2.
- •Пример решения задачи из задания № 2.
- •Задание № 3.
- •Пример решения задачи из задания № 3.
- •Задание № 4.
- •Пример решения задачи из задания № 4.
- •Задание № 7.
- •Пример решения задачи из задания № 7.
- •Задание № 8.
- •Пример решения задачи из задания № 8.
- •Задание № 9.
- •Пример решения задачи из задания № 9.
- •Задание № 10.
- •Пример решения задачи из задания №10.
- •Рекомендуемая литература
Задание № 7.
Найти общий интеграл дифференциального уравнения.
1.

2.

3.

4.
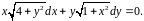
5.

6.

7.
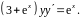
8.


9.

10.

Пример решения задачи из задания № 7.
В некоторых ситуациях обыкновенные дифференциальные уравнения первого порядка легко решаются с помощью приема, который мы будем называть методом разделения переменных. Поясним суть приема на примере. Пусть дано уравнение:

Постараемся преобразовать уравнение так, чтобы в левой его части было выражение, содержащее только переменную x, а в правой неизвестную функцию y.


Если мы умножим формально обе части равенства на dx, то получим выражения, которые можно трактовать как дифференциалы некоторых функций, зависящих только от x и от y:

Равенство дифференциалов предполагает, что сами функции отличаются друг от друга на некоторую константу С, т.е.

Окончательно получаем
 .
.
Подставляем полученную функцию в исходное уравнение, нетрудно убедиться, что уравнение превращается в тождество.
Задание № 8.
Найти общее решение дифференциального уравнения.
1.
 2.
2.

3.
 4.
4.
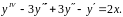
5.
 6.
6.
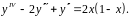
7.
 8.
8.

9.
 10.
10.

Пример решения задачи из задания № 8.
Найти общее решение дифференциального уравнения

Решение.
Имеем
линейное неоднородное дифференциальное
уравнение 3-го порядка с постоянными
коэффициентами (ЛНДУ). Его общее решение
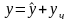 ,
где
,
где
 -
общее решение соответствующего
однородного уравнения (ЛОДУ),
-
общее решение соответствующего
однородного уравнения (ЛОДУ),
 - частное решение данного ЛНДУ. В нашем
случае ЛОДУ имеет вид:
- частное решение данного ЛНДУ. В нашем
случае ЛОДУ имеет вид:
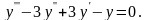
Характеристическое уравнение

Имеем
корень
 кратности 3, значит
кратности 3, значит

Далее находим частное решение исходного уравнения в виде:
 Так
как
Так
как
 ,
,
 -
число, равное кратности
-
число, равное кратности
 как корня характеристического уравнения,
то
как корня характеристического уравнения,
то
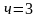 ,
поэтому
,
поэтому

Находим

Подставив
 в исходное уравнение и произведя
сокращения, получим 6А=2,
т.е.
в исходное уравнение и произведя
сокращения, получим 6А=2,
т.е.
 тогда
тогда
 а искомое общее решение примет вид
а искомое общее решение примет вид

Задание № 9.
Исследовать на сходимость ряд.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример решения задачи из задания № 9.
Исследуем
сходимость знакоположительного ряда
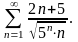
Решение.
Воспользуемся признаком Даламбера. Пусть для знакоположительного ряда существует предел отношения последующего члена к предыдущему

если
 то данный ряд сходится,
то данный ряд сходится,если
 то
данный ряд расходится,
то
данный ряд расходится,если
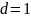 ,
то данный признак не дает ответа: ряд
может как сходится, так и расходится,
требуется дополнительное исследование.
Итак,
,
то данный признак не дает ответа: ряд
может как сходится, так и расходится,
требуется дополнительное исследование.
Итак,
 ,
,
Так
как
 то ряд
то ряд
 -
сходится.
-
сходится.