
- •Задание № 1.
- •Пример решения задачи из задания № 1
- •Задание № 2.
- •Пример решения задачи из задания № 2.
- •Задание № 3.
- •Пример решения задачи из задания № 3.
- •Задание № 4.
- •Пример решения задачи из задания № 4.
- •Задание № 7.
- •Пример решения задачи из задания № 7.
- •Задание № 8.
- •Пример решения задачи из задания № 8.
- •Задание № 9.
- •Пример решения задачи из задания № 9.
- •Задание № 10.
- •Пример решения задачи из задания №10.
- •Рекомендуемая литература
Министерство образования и науки РФ
Читинский институт (филиал) ФГБОУ ВПО
«Байкальский государственный университет экономики и права»
Кафедра математики
Контрольная работа
по дисциплине «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
для студентов 1-го курса
(бакалавров заочного отделения)
по направлению 080100.03 Экономика, профиль Финансы и кредит
по направлению 080100.04 Экономика, профиль Бухгалтерский учет, анализ и аудит
по направлению 080100.01 Экономика, профиль Экономика предприятия и предпринимательская деятельность
по направлению 080100.02 Экономика, профиль Мировая экономика
Чита, 2011г.
Печатается по решению УМК ЧИ (филиал) ФГБОУ ВПО
Протокол № ____ от ___________ 2011 г.
Составители: профессор, к.ф.-м.н. кафедры математики Линькова Г.Н.
ведущий доцент, к.ф.-м.н. кафедры математики Фалейчик А.А.
Рекомендовано к печати кафедрой математики
Протокол заседания № _1_ от _16 сентября_2011г.
Указания к выполнению контрольных работ:
По курсу «Математический анализ» каждый студент должен выполнить контрольную работу. Варианты заданий для этих работ приведены ниже.
При выполнении, оформлении контрольной работы необходимо руководствоваться следующим:
Контрольная работа должна быть выполнена по соответствующему варианту. В случае невыполнения этого требования автоматически ставиться «НЕЗАЧЕТ».
Условия задач необходимо переписать в работу. После условия каждой задачи следует ее решение. Ко всем этапам решения задач необходимо дать развернутые описательные пояснения.
В конце работы следует указать литературу (автора, название и год издания), использованную при ее выполнении, а также при изучении учебного материала. Студент должен подписать работу и поставить дату окончания ее выполнения.
На бланке, который наклеивается на обложку работы, четко пишется фамилия, имя, отчество студента, а также номер студенческого билета/зачетной книжкой.
Если работа не зачтена, то ее необходимо переделать в соответствии с указаниями, данными в рецензии.
Зачтенные контрольные работы обязательно предъявляются на экзамене.
Выбор варианта контрольной работы:
Если номер зачетной книжки оканчивается цифрой 1, следовательно, вариант контрольной работы 1и т.д.; если номер зачетной книжки оканчивается цифрой 0, вариант контрольной работы 10.
Пример: номер зачетной книжки № 02-36, вариант 6 по всем заданиям.
Задание № 1.
Решить систему линейных уравнений.
Дана
система уравнений:
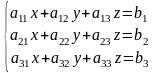 .
.
1.

2.
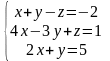
3.
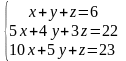
4.

5.

6.

7.

8.

9.

10.

Пример решения задачи из задания № 1
Решить
систему уравнений
 .
.
По правилу Крамера.
Если
главный определитель системы из
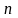 уравнений с
неизвестными отличен от 0, то система
имеет единственное решение, которое
ищется по формулам:
уравнений с
неизвестными отличен от 0, то система
имеет единственное решение, которое
ищется по формулам:
 .
.
Посчитаем
 ,
,
 и
и
 .
Каждый
из них получается из главного определителя
.
Каждый
из них получается из главного определителя
 системы заменой столбца коэффициентов
при неизвестном
системы заменой столбца коэффициентов
при неизвестном
 столбцом свободных членов уравнений,
стоящих в правой части системы:
столбцом свободных членов уравнений,
стоящих в правой части системы:


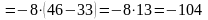 ,
,


Задание № 2.
Доказать,
что
 .
.
1.
 6.
6.

2.
 7.
7.

3.
 8.
8.
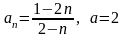
4.
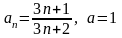 9.
9.

5.
 10.
10.
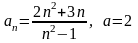
Пример решения задачи из задания № 2.
Доказать,
что
 .
.
Исходя
из определения предела последовательности,
для любого положительного числа
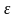 нужно найти такой номер
нужно найти такой номер
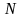 члена последовательности
члена последовательности
 ,
начиная с которого выполнилось бы
неравенство
,
начиная с которого выполнилось бы
неравенство
 .
.
В нашем случае можно поступить так:
 .
.
Отсюда
получаем, что
 .
.
Например,
достаточно выбрать число, на единицу
большее целой части дроби
 ,
т.е.
,
т.е.
 .
.
В
частности, если
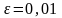 ,
то
можно взять равным 100.
,
то
можно взять равным 100.
Задание № 3.
а) Вычислить пределы функций.
1.
 2.
2.

3
 4
4

5
 6
6

7
 8
8

9
 10
10

б) Вычислить пределы функций.
1.
 2.
2.

3.
 4.
4.
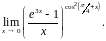
5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

Пример решения задачи из задания № 3.
Вычислить пределы, не пользуясь правилом Лопиталя.
В
числителе и знаменателе дроби стоят
многочлены 5-ой степени, каждый из
которых при
 являются бесконечно большими одного
порядка, т.е. получаем неопределенность
типа
являются бесконечно большими одного
порядка, т.е. получаем неопределенность
типа
 .
Однако, предел отношения двух многочленов
одинаковой степени при
равен отношению коэффициентов при
самой старшей степени (здесь
.
Однако, предел отношения двух многочленов
одинаковой степени при
равен отношению коэффициентов при
самой старшей степени (здесь
 ).
В данном случае это отношение равно
).
В данном случае это отношение равно
 .
Поэтому
.
Поэтому
 .
.
Действительно,
разделим числитель и знаменатель дроби
на старшую степень
 ,
а именно на
:
,
а именно на
:

При
дроби
 являются бесконечно малыми величинами,
т.е. их пределы при
равны 0.
являются бесконечно малыми величинами,
т.е. их пределы при
равны 0.
Воспользуемся такими свойствами пределов как:
 ,
,

в
предположении, что
 и
и
 существуют.
существуют.
Продолжим цепочку вычисления предела:

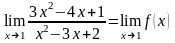 .
.
При
 числитель и знаменатель дроби обращаются
в 0, т.е.
является корнем многочленов, образующих
дробь. Следовательно, при
числитель и знаменатель дроби обращаются
в 0, т.е.
является корнем многочленов, образующих
дробь. Следовательно, при
 имеем неопределенность типа
имеем неопределенность типа
 .
Попробуем раскрыть ее.
.
Попробуем раскрыть ее.
Разложим оба многочлена на множители:

 .
.
Теперь искомый предел можно переписать следующим образом:

При
всех значениях
 ,
в том числе и в окрестности т.
,
отношение этих многочленов равно
,
в том числе и в окрестности т.
,
отношение этих многочленов равно
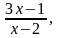 а в т.
функция
а в т.
функция
 не определена.
не определена.

 .
.
При
 получаем неопределенность типа
.
Распишем числитель дроби, как разность
кубов
получаем неопределенность типа
.
Распишем числитель дроби, как разность
кубов
 :
:
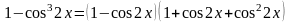 .
.
При
 ,
a
,
a
 ,
поэтому можем сделать следующие
выкладки:
,
поэтому можем сделать следующие
выкладки:
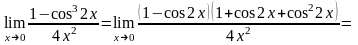

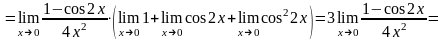
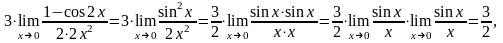
т.к.
 – это первый замечательный предел.
– это первый замечательный предел.
При


 получаем неопределенность вида
получаем неопределенность вида
 .
Раскроем ее. Выделим в основании степени
1:
.
Раскроем ее. Выделим в основании степени
1:
 .
.
При
слагаемое
 является бесконечно малой, т.е. ее
предел равен 0. Поэтому воспользуемся
вторым замечательным пределом:
является бесконечно малой, т.е. ее
предел равен 0. Поэтому воспользуемся
вторым замечательным пределом:
 .
.
Здесь
 ,
поэтому
,
поэтому


т.к.
 (отношение коэффициентов при старшей
степени).
(отношение коэффициентов при старшей
степени).
Ответ:
 .
.


