5. Моделирование системы автоматического управления средствами matlab

5.1. Исследование непрерывной системы.

Проведём моделирование системы автоматического управления средствами программного пакета MATLAB (рис.12). Воспользуемся расширением данного программного продукта – средой моделирования Simulink [1].

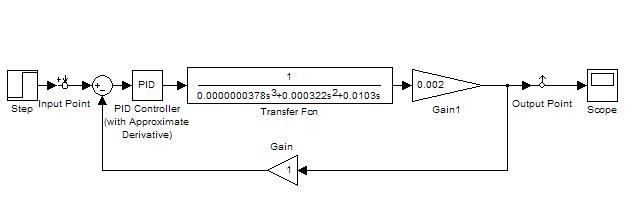
Рис. 12. Модель системы автоматического управления в среде Simulink

Используя встроенные средства среды Simulink, получим график переходного процесса системы, при воздействии на неё единичного ступенчатого сигнала (рис. 13).

Из графика можем определить следующие параметры система автоматического управления:

• величина статической ошибки – 0%;

• время переходного процесса –30 с;

• колебательность присутствует;

• коэффициент перерегулирования – 55.5%.

Исходя из этих данных, можно сделать вывод о том, что система автоматического управления не соответствует техническому заданию (по пунктам коэффициент перерегулирования, время переходного процесса и колебательность системы) и нуждается в корректировке. В качестве корректирующего звена выберем ПИД (пропорционально-интегрально-дифференциальный) регулятор.

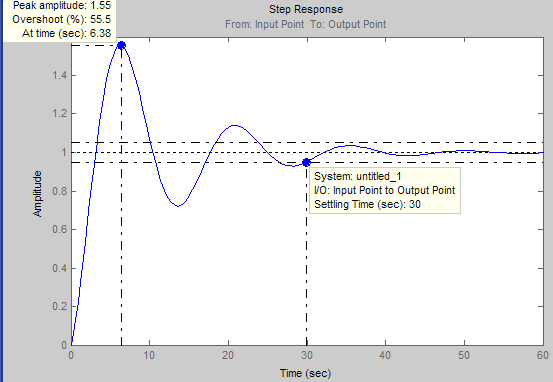
Рис. 13. График переходного процесса системы при воздействии на неё единичного ступенчатого сигнала

5.2. Настройка пид - регулятора.

Для настройки ПИД регулятора – определения значений пропорционального, дифференциального и интегрального коэффициентов – воспользуемся встроенными средствами среды Simulink.

Подбор коэффициентов будем осуществлять с помощью блока NCD OutPort. Включим его в схему, как показано на рисунке 27.

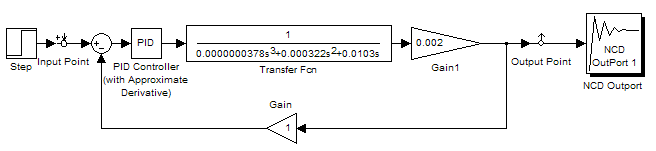
Рис. 14. Схема, собранная для настройки ПИД регулятора

Зададим настройки блока NCD OutPort (рис. 15 16) и ПИД регулятора PID Controller (рис. 17).

Рис. 15. Настройки блока NCD OutPort

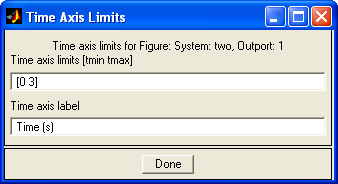
Рис. 16. Настройки блока NCD OutPort

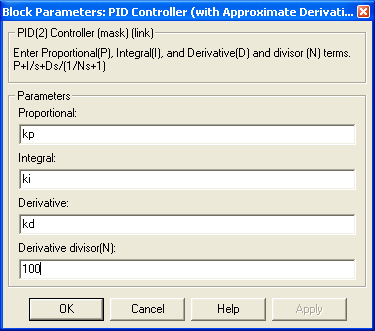
Рис. 17. Параметры ПИД регулятора PID Controller

В блоке NCD OutPort зададим ограничения для графика переходного процесса (рис. 18).

Блок NCD OutPort производит автоматическую коррекцию параметров Kp, Ki и Kd.

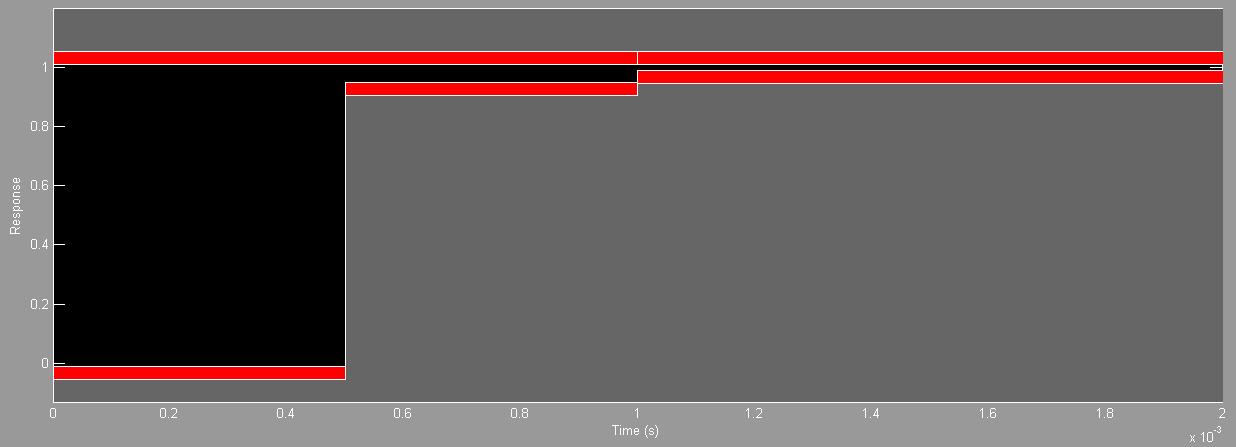
Рис. 18. Настройка границ в блоке NCD OutPort

Значения коэффициентов, полученных оптимизацией в блоке NCD OutPort:

Kp =64.48

Ki = 0, 025

Kd = 1, 12

После корректировки переходная функция удовлетворяет техническому заданию (рис. 19).

Получены следующие характеристики:

Время переходного процесса – 0.207 с.

Количество колебаний – 0.

Коэффициент перерегулирования – 0.

Статическая ошибка – 0.004.

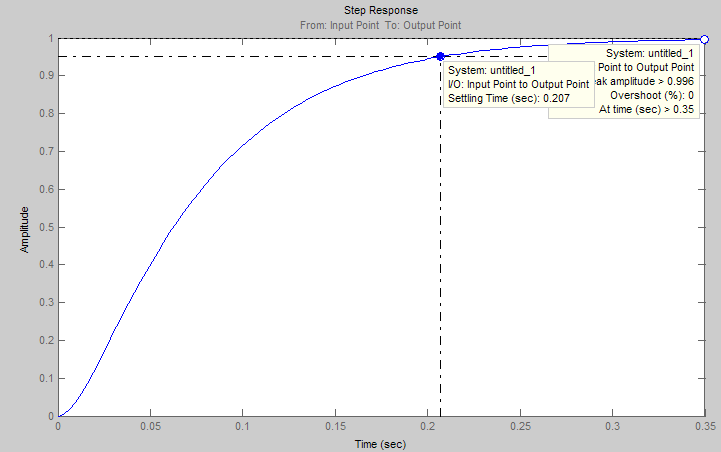
Рис. 19. Реакция системы на единичное ступенчатое воздействие

5.3. Определение передаточных функций разомкнутой и замкнутой системы.

Определим передаточную функцию разомкнутой системы:

W_раз = W_ус (p) ∙ W_{двигателя} (p) ∙ W_{редуктора} (p) ∙ W_{ПИД-регулятора} (p) (12)

(13)

Определим передаточную функцию замкнутой системы:

( 14)

(15)

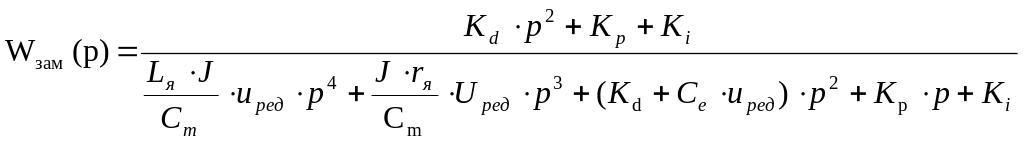
(16)

Характеристическое уравнение замкнутой системы имеет вид:

( 17)

5.4. Моделирование цифровой системы.

Для исследования ЦСАУ необходимо провести z-преобразование передаточной функции непрерывной системы. Для этого воспользуемся средствами математического пакета VisSim (рис. 20).

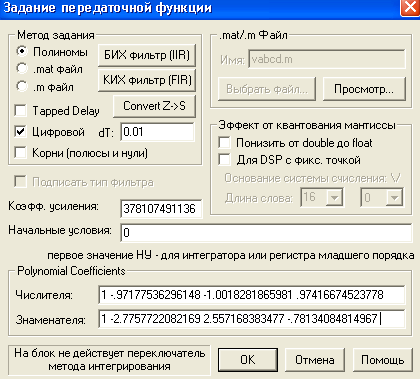
Рис. 20. Переход в Z-пространство средствами VisSim

Итогом этого преобразования станет дискретная передаточная функция (рис. 21).

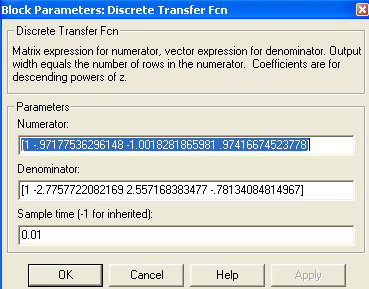
Рис. 21. Дискретная передаточная функция, полученная средствами VisSim

Смоделируем схему цифровой и замкнутую системы автоматического управления в Simulink (рис. 22).

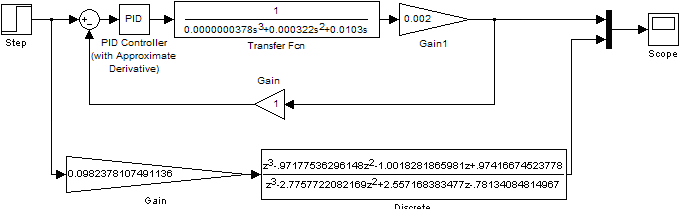
Рис. 22. Структурная схема цифровой и замкнутой системы.