9. Отношение к риску.

Попадая в одни и те же рискованные ситуации, индивиды демонстрируют тем не менее весьма различные стратегии поведения. Следовательно, наряду с различиями в степени рискованности лотерей внимания заслуживают и различия в отношении различных индивидов к риску. Самая общая классификация предполагает деление экономических агентов на три основные группы: не склонные, склонные и нейтральные к риску.

• Индивид, не склонный к риску, всегда предпочтет участию в игре гарантированное получение суммы, соответствующей математическому ожиданию выигрыша:

u(E(W)) > Eu .

• Индивид, склонный к риску, всегда предпочтет участие в игре гарантированному получению суммы, соответствующей математическому ожиданию выигрыша:

u(E(W)) < Eu

Рис.2.5. а Индивид не склонен к риску( is globally risk-averse). Функция полезности вогнутая: < 0

Рис.2.5.б Индивид склонен к риску( is globally risk-lover). Функция полезности выпуклая: > 0

• Нейтральность к риску (risk-neutrality), т.е. безразличие между участием в справедливой игре и гарантированным получением суммы, соответствующей математическому ожиданию выигрыша: u(E(W)) = Eu ,предполагает линейность функции Бернулли : u(W) = a + bW, u "(W) = 0

Рис.2.5.в Индивид нейтрален к риску( is globally risk-neutral). Функция полезности линейна: = 0

Итак:

несклонность к риску	u '(W) > 0; u "(W) < 0	u(W) вогнутая
склонность к риску	u '(W) > 0; u "(W) > 0	u(W) выпуклая
нейтральность к риску	u '(W) > 0; u "(W) = 0	u(W) линейнaя

Несложно догадаться, что характер функции u(W), т.е. ее вогнутость, либо выпуклость, не может не сказаться и на виде кривых безразличия функции ожидаемой полезности. И это действительно так, в чем можно убедиться перейдя, в частности, к рассмотрению уже упоминавшегося треугольника Маршака- Мaшина( the Marschak-Machina triangle).

Наряду с кривыми безразличия, т.е. прямыми линиями, соответствующими заданному уровню ожидаемой полезности, изобразим в треугольнике Маршака- Машина и так называемые линии постоянного ожидаемого выигрыша (iso-expected value lines), представляющие собой совокупность точек, соответствующих лотереям с одинаковым математическим ожиданием выигрыша:

= const ; =1 Þ p₃ = const + [ ] p₁

Полученное выражение свидетельствует о том, что линии постоянного ожидаемого выигрыша (также как и кривые безразличия) будут параллельными прямыми линиями, имеющими положительный наклон при w₁ < w₂ < w₃ .

Именно соотношение наклонов кривых безразличия и кривых постоянного ожидаемого выигрыша, и будет характеризовать отношение индивида к риску.

Рассмотрим два треугольника Маршака- Машина , на которых пунктиром обозначены линии постоянного ожидаемого выигрыша( iso-expected value lines), а непрерывными линиями - кривые безразличия.

Рис.2.6.а Индивид не склонен к риску.

Рис.2.6.б Индивид склонен к риску.

Cдвигу вдоль линий постоянного ожидаемого выигрыша к северо- востоку, соответствует повышение степени рискованности лотереи - при том же математическом ожидании выигрыша сокращается вероятность выигрыша промежуточного приза( w₂) при росте вероятностей выигрыша большего(w₃) и меньшего (w₁) призов. Уместно предположить, что для индивида, не склоненного к риску, подобного рода перемещение в треугольнике Маршака-Машина должно сопровождаться сокращением уровня получаемой им полезности, и, соответственно, его кривые безразличия имеют более крутой наклон, чем линии постоянного ожидаемого выигрыша(Рис.2.6.а ).

В противном случае, когда кривые безразличия являются более пологими, чем линии постоянного ожидаемого выигрыша , индивид отчетливо демонстрирует склонность к риску(Рис.2.6.б ). Нейтральность к риску предполагает совпадение углов наклона кривых постоянного ожидаемого выигрыша и кривых безразличия.

Иначе отношение индивида к риску скажется на кривых безразличия, изображаемых на пространстве условных благ. Набору условных благ соответствует точка, координаты которой характеризуют уровни благосостояния в различных состояниях(Wg и W_b будут соответствовать "богатству" в хорошие и плохие времена).

Для индивидов, не склонных к риску, кривые безразличия функции ожидаемой полезности кривые Eu = 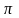u(W_b)+(1 - )u(W_g) будут иметь традиционный (выпуклый) вид, поскольку при увеличении потребления условного блага Wg значения предельной нормы замещения

MRS = =

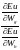будут убывать. В сущности, можно было ограничиться указанием на то, что функция ожидаемой полезности, представляющая собой выпуклую комбинацию вогнутых функций, также должна обладать свойством вогнутости, а , следовательно - и квазивогнутости, что, в свою очередь, предполагает убывание предельной нормы замещения. Иначе тот же результат можно получить, взяв производную MRS по W_g (это выражение неоднократно будет использовано впоследствии):

= [ (1- ) / u '(W_b)² ] { [u ''(W_g)u '(W_b)] - [u '(W_g)u ''(W_b)(dW_b/dW_g)] }

Заметим, что знак этой производной будет определяться знаком выражения в фигурных скобках (первый сомножитель заведомо положителен), а он (ввиду вогнутости функции Бернулли: u ''(W)< 0) будет негативным.

Нейтральность к риску предполагает линейность кривых безразличия и совпадение резервной кривой безразличия с кривой постоянного ожидаемого выигрыша:

MRS = =

а склонность к риску графически будет иллюстрироваться кривыми безразличия, при движении вдоль которых MRS будет возрастать: при увеличении Wg числитель дроби

будет возрастать одновременно с убыванием знаменателя.

Рис.2.7.а Несклонность к риску.

Рис.2.7.б Нейтральность к риску.

Рис.2.7.в Склонность к риску.6

Обычно полагается, что индивид не склонен к риску. Подтверждением тому служит, в частности, стремление индивида дивеpсифицировать свой портфель. Действительно, нейтральный к риску индивид стремился бы вложить свои сбережения в ценные бумаги, обеспечивающие максимальное математическое ожидание дохода, в то время как диверсификация портфеля, гарантирующая индивида от провально низких уровней дохода за счет потери части ожидаемого дохода, является своего рода страховой премией, уплачиваемой не склонным к риску индивидом.