
- •1.1 Приведение моментов сопротивления и сил, моментов инерции и масс к валу электродвигателя. Учёт потерь в передачах.
- •1.3. Механические переходные процессы при линейном динамическом моменте.
- •1.4. Тормозные режимы дпт независимого возбуждения.
- •1.5. Мех. И эл.Мех. Характеристики асинхронного двигателя.
- •1.6. Тормозные режимы работы асинхронного двигателя.
- •1.7. Эл.Мех. Перех. Процессы при набросе и сбросе нагрузки эп
- •1.8. Механические переходные процессы электропривода с линейной механической характеристикой при линейном задании скорости идеального холостого хода.
- •1.9. Потери мощ. В установившихся реж. Раб. Нерег. Эп и рег .
- •1.11. Потери энергии в переходных процессах электроприводов при линейном изменении скорости идеального холостого хода
- •Потери энергии за время переходного процесса
- •Подставив (6.168) в (6.167), получим , (6.169)
- •1.12. Нагрев и охл. Эд. Типовые режимы работы электропривода
- •Аналогично имеем для уравнения (7.11) тепловой модели , (7.16)
- •Аналогично можно записать дифференциальное уравнение для нагрева статора
- •1.13. Выбор мощ. Эд для продолжительного режима работы с неизменной нагрузкой. (режим s1) и переменной.
- •Принимая во внимание (6.17), отношение (7.92) можно записать в виде
- •Для ном. Реж. Можно записать равенство
- •При переходе к пределам в (7.118) получаем
- •Продифференцировав (7.122), получим
- •1.14. Выбор мощ. Эд для повторно-кратковр реж. Раб. (s3, s4, s5).
- •1.15 Регулирование скор. Ад в системе «полупроводниковый преобразователь переменного напряжения – ад»
- •Обозначим
- •1.16. Pеостатное регулирование скорости асинхронного двигателя с фазным ротором
- •Подставляя (8.149) в (8.151) , находим (8.152)
1.9. Потери мощ. В установившихся реж. Раб. Нерег. Эп и рег .
НЕРЕГУЛИРУЕМЫЕ ЭП
Потери
мощ. в нерег. ЭП складываются из потерь
мощ. в ЭД
 и в мех. передаче
и в мех. передаче
 :
:
 (6.1). Потери мощ. в ЭД разделяют на
постоянные
(6.1). Потери мощ. в ЭД разделяют на
постоянные
 и переменные
и переменные
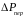 :
:
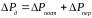 (6.2) Под пост. понимаются потери мощ.,
независящие от нагрузки: 1) потери
в стали, 2) мех. потери, 3) вентиляц.
потери, 4) потери на возб. ЭД. Под
переем. потерями
понимают потери мощ., зависящие от
нагрузки, т. е. потери в проводниках
обмоток, по которым протекает ток
нагрузки.
(6.2) Под пост. понимаются потери мощ.,
независящие от нагрузки: 1) потери
в стали, 2) мех. потери, 3) вентиляц.
потери, 4) потери на возб. ЭД. Под
переем. потерями
понимают потери мощ., зависящие от
нагрузки, т. е. потери в проводниках
обмоток, по которым протекает ток
нагрузки.
Для двигателей постоянного тока:
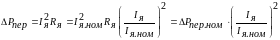 ,(6.4)
,(6.4)
где
 , (6.5)
– ном. пер. потери мощ.,
, (6.5)
– ном. пер. потери мощ.,
 – Σ сопр. якорной цепи.
– Σ сопр. якорной цепи.
Для асинхронных трехфазных двигателей:
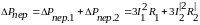 , (6.6)где
, (6.6)где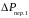 ,
,
 – соотв. потери мощ. в обмотках статора
и ротора;
– соотв. потери мощ. в обмотках статора
и ротора; ,
,
 – активные сопр. фаз статора и ротора
– активные сопр. фаз статора и ротора
При
небольшом диапазоне изм. токов АД, когда
намагн. ток
 примерно постоянный, можно принять:
примерно постоянный, можно принять:
 (6.7) Тогда переем. потери в трехфазной
обмотке статора:
(6.7) Тогда переем. потери в трехфазной
обмотке статора: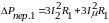 .
Составляющую потерь
.
Составляющую потерь
 можно отнести к постоянным потерям ( на
возбуждение), а переменные потери АД
выразить через ток ротора
можно отнести к постоянным потерям ( на
возбуждение), а переменные потери АД
выразить через ток ротора
 ,(6.9)
,(6.9)
где
 (6.10).
(6.10).
Для трех фазных синхронных двигателей:
 ,(6.11)
,(6.11)
где
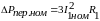 .Если
ввести коэффициент загрузки
.Если
ввести коэффициент загрузки
 (6.13), то переменные
потери для любого ЭД можно записать в
виде
(6.13), то переменные
потери для любого ЭД можно записать в
виде
 (6.14)
Суммарные потери мощности в
электродвигателе
(6.14)
Суммарные потери мощности в
электродвигателе
 (6.15)
Обозначим
(6.15)
Обозначим
 (6.16)
как коэффициент потерь, который зависит
от ном. мощ., ном. скор. и конструкции ЭД
и в общем случае находится в пределах
0,52, тогда с учетом
(6.16) суммарные потери мощности в ЭД
запишем в виде
(6.16)
как коэффициент потерь, который зависит
от ном. мощ., ном. скор. и конструкции ЭД
и в общем случае находится в пределах
0,52, тогда с учетом
(6.16) суммарные потери мощности в ЭД
запишем в виде
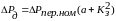 (6.17)
(6.17)
Для наглядного представления потерь мощности приведем энергетические диаграммы ДПТ НВ (рис.6.1) и АД (рис.6.2).
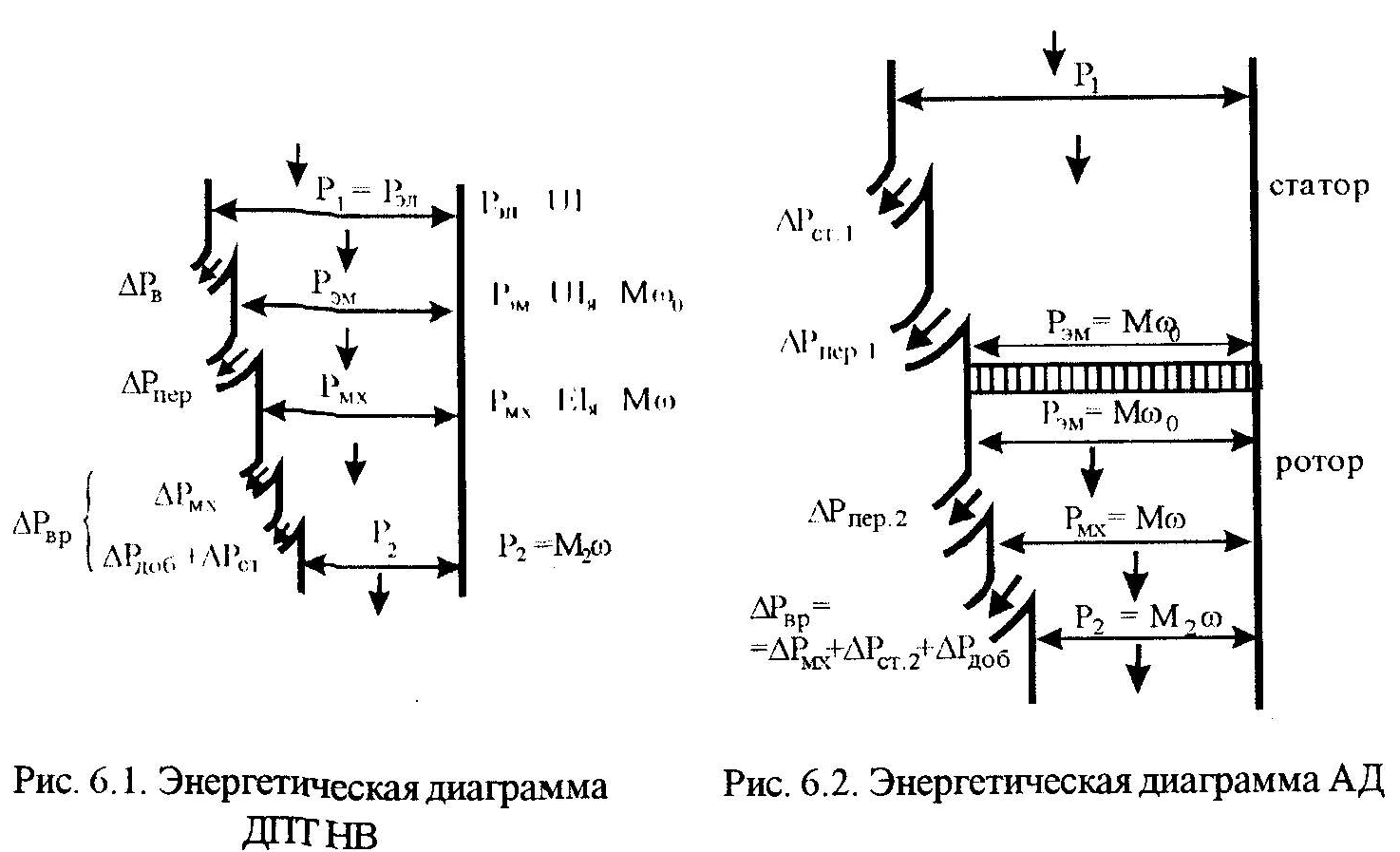
Мех. хар-ки ДПТ НВ и АД в пределах рабочей зоны в установившемся реж. можно считать линейными Как можно видеть из энергетических диаграмм ДПТ НВ и АД и рис.6.3, переменные потери в якоре ДПТ НВ и в роторе
 (6.18)
(6.18)
где
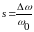 (6.19)
(6.19)
 (6.20) Суммарные переменные потери для АД
(6.20) Суммарные переменные потери для АД
 , (6.21)
где
, (6.21)
где
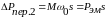 (6.22)
(6.22)
Переменные потери мощ. в ЭД с линейной мех. хар-кой пропорциональны скольжению.
Колебания скорости и момента приводят к увеличению потерь мощности.
РЕГУЛИРУЕМЫЕ ЭП
Для регулируемых ЭП постоянного тока постоянные потери мощ. представляют в виде:
 (6.29)
(6.29)
где Рв.ном – номинальные потери мощности на возбуждение,
m – показатель, характеризующий кривую намагничивания, 1<m<2.
Переменные
потери в регулируемых ЭП постоянного
тока выражаются формулой
 ,
в рег. ЭП постоянного тока к потерям в
ЭД Рд добавляются
потери мощ. в преобр. Рпр,
которые тоже разделяют на постоянные
(потери в стали силовых трансф.) Рпост.пр
и переменные (потери в обмотках трансф.,
дросселей) Рпер.пр:
,
в рег. ЭП постоянного тока к потерям в
ЭД Рд добавляются
потери мощ. в преобр. Рпр,
которые тоже разделяют на постоянные
(потери в стали силовых трансф.) Рпост.пр
и переменные (потери в обмотках трансф.,
дросселей) Рпер.пр:
 (6.30)
(6.30)
где
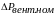 – ном. потери в вентилях преобр.,
– ном. потери в вентилях преобр.,
 – потери короткого замыкания в трансф.,
– потери короткого замыкания в трансф.,
 – потери в дросселях,
– потери в дросселях,
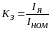 – коэффициент загрузки. Постоянные
потери мощ. в регул. АД вкл. потери в
стали статора Рст.1,
потери в стали ротора Рст.2,
потери в обмотке статора от протекания
намагн. тока Р
и механические потери Рмх:
– коэффициент загрузки. Постоянные
потери мощ. в регул. АД вкл. потери в
стали статора Рст.1,
потери в стали ротора Рст.2,
потери в обмотке статора от протекания
намагн. тока Р
и механические потери Рмх:
 (6.31).В свою очередь мех. потери принимают
пропорц. квадрату скорости
(6.31).В свою очередь мех. потери принимают
пропорц. квадрату скорости (6.32)
из-за преобладающего влияния вентиляционных
потерь. Потери в стали статора АД можно
записать в виде
(6.32)
из-за преобладающего влияния вентиляционных
потерь. Потери в стали статора АД можно
записать в виде
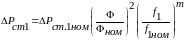 , (6.33)
где Ф, Фном – текущее и ном. значение
магн. потока,f1, f1ном
– текущее и ном. значение частоты тока
статора,m – показатель
степени, принимающий значение m=1,31,5
в зависимости от сорта электротехнической
стали.
, (6.33)
где Ф, Фном – текущее и ном. значение
магн. потока,f1, f1ном
– текущее и ном. значение частоты тока
статора,m – показатель
степени, принимающий значение m=1,31,5
в зависимости от сорта электротехнической
стали.
Потери в стали ротора зависят от частоты (скольжения s) тока ротора:
 (6.34)
Потери от протекания намагн. тока I
по обмотке статора можно выразить таким
образом:
(6.34)
Потери от протекания намагн. тока I
по обмотке статора можно выразить таким
образом:
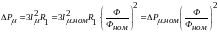 ,(6.35)где
,(6.35)где ,(6.36)
,(6.36)
Как будут изменяться составляющие постоянных потерь регулируемого АД, будет зависеть от способа регулирования.
При реостатном способе регулирования АД имеем:
 ,поэтому
постоянные потери
,поэтому
постоянные потери
 (6.37)
остаются примерно постоянными, т.к.
возрастание потерь в стали при увел.
скольжения ротора примерно компенсируется
уменьшением мех. потерь из-за уменьшения
скорости.
(6.37)
остаются примерно постоянными, т.к.
возрастание потерь в стали при увел.
скольжения ротора примерно компенсируется
уменьшением мех. потерь из-за уменьшения
скорости.
При част. упр. АД по одному из законов стабилиз. Потокосц. (статора, взаимоиндукции или ротора) магнитный поток ФФном, а абсолютное скольж. sа обычно поддерживается на низком уровне (в пределах ном. на естественной хар-ке), что позволяет пренебречь потерями в стали ротора и считать скор. пропорц. частоте. В результате, при частотном упр. АД по закону Ф=const постоянные потери можно записать в виде
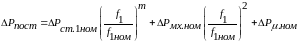 (6.38)
(6.38)
Переменные потери мощ. при частотном упр. АД определяются выраж. (6.21) – (6.22):
 ,
где
,
где
 (6.40)
(6.40)
sа
– абсолютное скольжение, w0ном
– синхронная угловая скор. АД при ном.
частоте, – модуль
жесткости мех. хар-ки, который для
линейной (линеаризованной) хар-ки равен
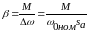 .
В теории част. упр. обычно применяют
обозначения
.
В теории част. упр. обычно применяют
обозначения
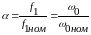 (6.41)
(6.41)
 (6.42)
тогда
(6.42)
тогда
 (6.42)
(6.42)
При
реостатном регул. АД дело обстоит
по-другому. Переменные потери в статоре
АД при реостатном регулировании
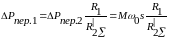 ,
(6.43), где
,
(6.43), где
 –приведенное
Σ активное сопр. фазы ротора.
–приведенное
Σ активное сопр. фазы ротора.
 , (6.44),где
sе – скольжение на
ест. мех. хар-ке АД при данном эл.магн.
М,
, (6.44),где
sе – скольжение на
ест. мех. хар-ке АД при данном эл.магн.
М,
 – приведенное собственное активное
сопр. фазы ротора. Подставив в (6.44) в
(6.43), получим
– приведенное собственное активное
сопр. фазы ротора. Подставив в (6.44) в
(6.43), получим
 ,
переменные потери в обмотке статора АД
при реостатном регул. и неизменном М на
валу являются постоянными, независящими
от скор. Переменные же потери в роторе
АД при постоянном моменте
,
переменные потери в обмотке статора АД
при реостатном регул. и неизменном М на
валу являются постоянными, независящими
от скор. Переменные же потери в роторе
АД при постоянном моменте
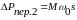 ,
(6.46) будут пропорциональные скольж.,
т.е. будут увелич. со сниж. скор.
,
(6.46) будут пропорциональные скольж.,
т.е. будут увелич. со сниж. скор.
1.10. ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭП ПРИ ПОСТОЯННОЙ ВЕЛИЧИНЕ СКОР. ИДЕАЛЬНОГО ХХ (Ω0=CONST).
Потери
энергии в переходных процессах
электропривода зависят от системы
электропривода и способа формирования
переходного процесса и в общем случае
определяются выражением
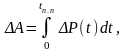 (6.120)
(6.120)
где ΔP(t) – суммарные потери мощности в данный момент времени переходного процесса, tП.П. – время переходного процесса.
Главнейшим фактором, определяющим потери энергии в переходном процессе, является характер изменения скорости ω0 идеального холостого хода.
В электроприводах с ω0=const управляющее воздействие изменяется скачком. Потери энергии, вызванные механическим переходным процессом, значительно превосходят потери энергии от электромагнитного переходного процесса. Поэтому при оценке потерь энергии в переходных процессах будет учитывать только механические переходные процессы. Постоянные потери в переходных процессах электропривода составляют менее 5% от суммарных потерь. Поэтому в переходных процессах электропривода будем учитывать потери энергии только от переменных потерь мощности. Потери мощности в якорной цепи ДПТ НВ и в роторной цепи АД: ΔР= РЭМ – РМХ=М(ω0–ω) (6.121)
Соответственно потери энергии будут равны разности электромагнитной А1 и полной механической А2 энергий электропривода: ΔА= А1 – А2 (6.122)
где 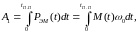 (6.123)
(6.123)
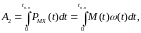 (6.124)
(6.124)
Р ассмотрим
частный случай при МС=0:
М=МДИН=J
, (6.125),что
при подстановке в (6.123) и (6.124) приводим
к результату
ассмотрим
частный случай при МС=0:
М=МДИН=J
, (6.125),что
при подстановке в (6.123) и (6.124) приводим
к результату
 (6.126)
(6.126) (6.127), где ω1
и ω2
– угловые скорости электродвигателя
в начале и в конце переходного процесса,
J
– суммарный момент электропривода,
приведенный к валу электродвигателя.
(6.127), где ω1
и ω2
– угловые скорости электродвигателя
в начале и в конце переходного процесса,
J
– суммарный момент электропривода,
приведенный к валу электродвигателя.
Произведение Jω есть момент количества движения и имеет размерность H·м·с·рад.
Потери
энергии в электроприводе при изменении
угловой скорости ротора от ω1
до ω2
можно записать в виде
 (6.131) где L1(ω)=Jω0,
(6.132) L2(ω)=Jω,
(6.133)
(6.131) где L1(ω)=Jω0,
(6.132) L2(ω)=Jω,
(6.133)
L1(ω),
L2(ω)
– моменты количества движения
электропривода при угловой скорости
ω0
идеального холостого хода и текущей
угловой скорости ω.Соотношение (6.131)
можно представить графически (рис.
6.11). Как следует из рис. 6.11, потери энергии
в электроприводе при изменении скорости
от ω1
до ω2
равны площади трапеции BCFE,
так как А1=пл.ABCD,
А2=пл.AEFD.
Возьмем интегралы:
 (6.134)
(6.134)
 (6.135) где Δω = ω2
– ω1
(6.136), ωсρ=
½(ω2
+ ω1)
(6.137) В результате можем записать общую
формулу для определения потерь энергии
в якорной (роторной) цепи электропривода
за время переходного процесса при
ω0=const
и МС=0:
ΔА0
= JΔω(ω0
– ωсρ)
(6.138). Рассмотрим частные случаи потерь
энергии в переходных процессах
электропривода при ω0=const
и МС=0.
(6.135) где Δω = ω2
– ω1
(6.136), ωсρ=
½(ω2
+ ω1)
(6.137) В результате можем записать общую
формулу для определения потерь энергии
в якорной (роторной) цепи электропривода
за время переходного процесса при
ω0=const
и МС=0:
ΔА0
= JΔω(ω0
– ωсρ)
(6.138). Рассмотрим частные случаи потерь
энергии в переходных процессах
электропривода при ω0=const
и МС=0.
Пуск вхолостую: ω1=0; ω2=ω0; ωсρ= ½(ω2 + ω1)= ½ ω0; Δω = ω2 – ω1= ω0.
Н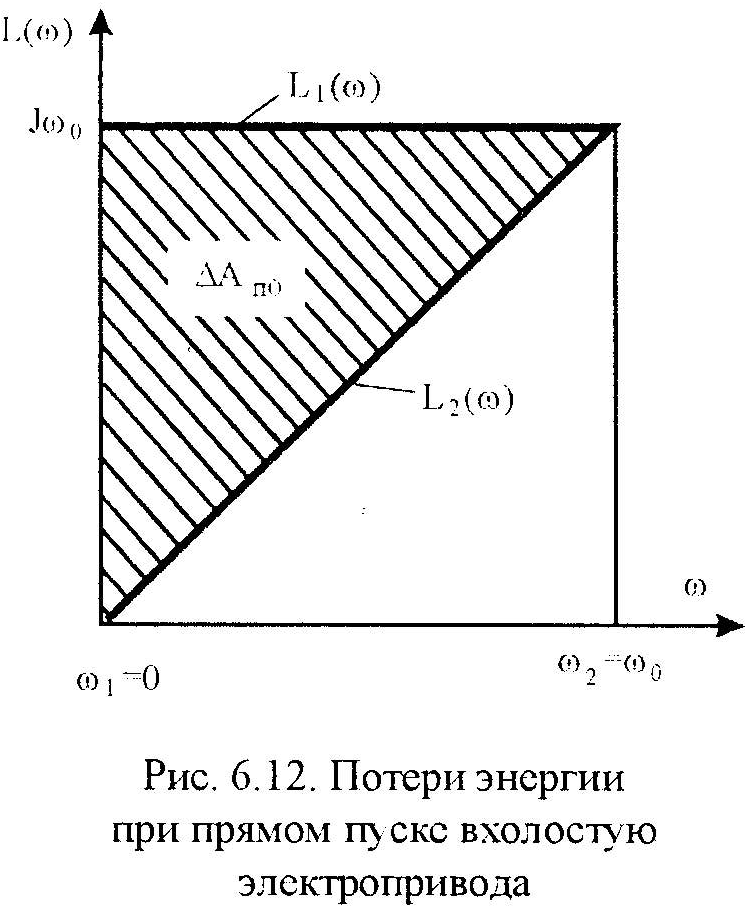 аходим
А1=Jω0Δω=J
аходим
А1=Jω0Δω=J ;
А2=JωсρΔω=
½ J
;
ΔАпо=А1
– А2=J
– ½ J
=
;
А2=JωсρΔω=
½ J
;
ΔАпо=А1
– А2=J
– ½ J
=
 .
.
К ак
видно, потери энергии при пуске
электропривода вхолостую равны половине
электромагнитной энергии, потребляемой
электроприводом, или равны запасу
кинетической энергии электропривода
независимо от времени пуска или каких-либо
схемных решений (рис. 6.12)
ак
видно, потери энергии при пуске
электропривода вхолостую равны половине
электромагнитной энергии, потребляемой
электроприводом, или равны запасу
кинетической энергии электропривода
независимо от времени пуска или каких-либо
схемных решений (рис. 6.12)
Динамическое торможение вхолостую:
ω1=ω0; ω2=0; ωсρ= 0,5(ω2 + ω1)= 0,5ω0; Δω = ω2 – ω1= –ω0.
Т ак
как при динамическом торможении якорь
электродвигателя отключен от силовой
цепи, то L1(ω)=0;
А1=0.Полная
механическая мощность: А2=JωсρΔω=
–½ J
и потери энергии ΔАдто=А1
– А2=0–(-½
J
)=
ак
как при динамическом торможении якорь
электродвигателя отключен от силовой
цепи, то L1(ω)=0;
А1=0.Полная
механическая мощность: А2=JωсρΔω=
–½ J
и потери энергии ΔАдто=А1
– А2=0–(-½
J
)=
 .Следовательно,
при динамическом торможении вхолостую
потери энергии равны запасу кинетической
энергии электропривода, так как при
динамическом торможении теряется вся
накопленная механическая энергия
(рис.6.13). поэтому при динамическом
торможении вхолостую потери энергии
равны потерям энергии при пуске вхолостую.
.Следовательно,
при динамическом торможении вхолостую
потери энергии равны запасу кинетической
энергии электропривода, так как при
динамическом торможении теряется вся
накопленная механическая энергия
(рис.6.13). поэтому при динамическом
торможении вхолостую потери энергии
равны потерям энергии при пуске вхолостую.
Торможение противовключением вхолостую:
ω1=ω0; ω2=0; ω0<0; ωсρ= 0,5(ω2 + ω1)= 0,5ω0; Δω = ω2 – ω1=0–ω0= –ω0.
Вычисляем: А1=Jω0Δω=J(-ω0)(-ω0)=J ; А2=JωсρΔω= ½ J (-ω0)= –½J ;
ΔАпр.о=А1
– А2=J
–(–½ J
)=
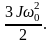
О тсюда
видно, что потери энергии при торможении
электропривода противовключением
вхолостую в три раза больше потерь
энергии при пуске или динамическом
торможении вхолостую (рис. 6.14).
тсюда
видно, что потери энергии при торможении
электропривода противовключением
вхолостую в три раза больше потерь
энергии при пуске или динамическом
торможении вхолостую (рис. 6.14).
Реверс вхолостую:
ω1=ω0; ω2= –ω0; ω0<0; ωсρ= 0,5(ω2 + ω1)= 0; Δω = ω2 – ω1= –2ω0.
Определяем: А1=Jω0Δω=J(-ω0)(-2ω0)=2J ;
А2=JωсρΔω= J·0·(-2ω0)=0;
ΔАрев.о=А1– А2=2J =
=
Потери энергии при реверсе электропривода вхолостую равны сумме потерь энергии при торможении противовключением и пуске вхолостую (рис.6.15).
Полученные
соотношения соответствуют потерям
энергии в якоре ДПТ НВ и в роторе АД.
Потери энергии ΔА1
в статоре АД определяются через потери
ΔА2
в роторе таким образом
 (6.139)
(6.139)
Т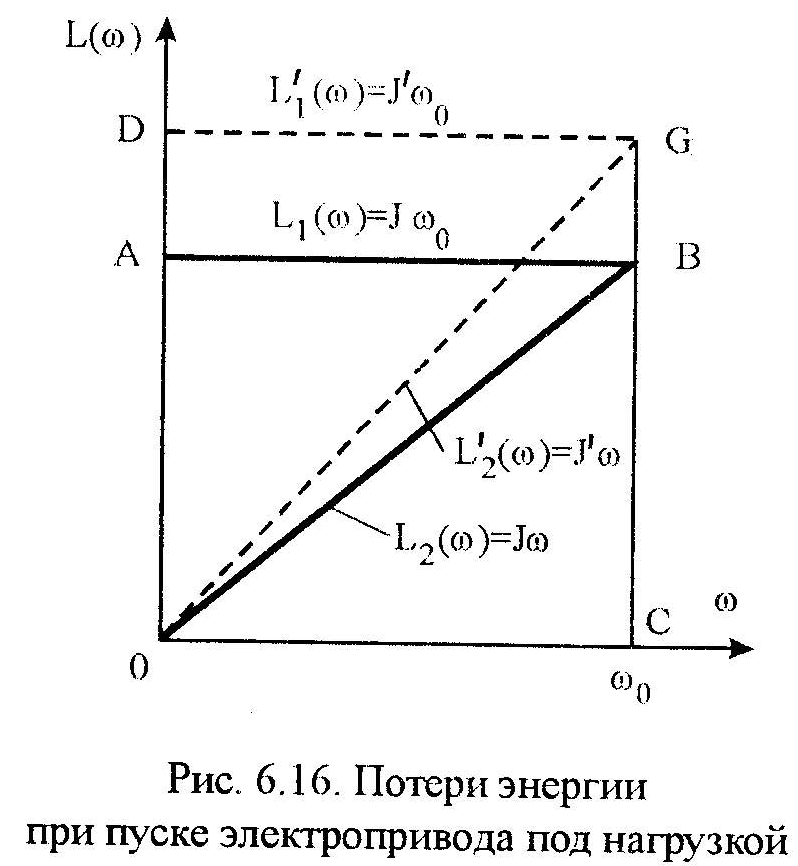 еперь
можно записать суммарные потери энергии
в асинхронном двигателе в переходном
процессе электропривода вхолостую:
еперь
можно записать суммарные потери энергии
в асинхронном двигателе в переходном
процессе электропривода вхолостую:
 (6.140)
(6.140)
Где (6.141)
(6.141)
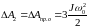 (6.142)
(6.142)
В
переходных процессах электропривода
с ω0=const
электромагнитный момент не остается
постоянным. Поэтому для оценки потерь
энергии в переходных процессах
электропривода с постоянным статическим
моментом (МС=const)
примем допущение, что в переходном
процессе электромагнитный момент
электродвигателя равен его среднему
значению МСР.
Тогда динамический момент
 (6.143) и скорость двигателя в переходном
процессе изменяется по линейному
закону
(6.143) и скорость двигателя в переходном
процессе изменяется по линейному
закону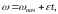 (6.144)где
(6.144)где (6.145) есть угловое ускорение
электродвигателя. При принятых допущениях
имеем М(t)=Мср=
Мс+
Мдин
(6.146)
(6.145) есть угловое ускорение
электродвигателя. При принятых допущениях
имеем М(t)=Мср=
Мс+
Мдин
(6.146)
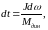 (6.147) что позволяет подинтегральные
выражения в (6.123) и (6.124) записать в виде
(6.147) что позволяет подинтегральные
выражения в (6.123) и (6.124) записать в виде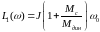 (6.148)
(6.148)
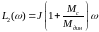 (6.149)Обозначим
(6.149)Обозначим
 (6.150),тогда действие статического момента
(в рамках принятых допущений) в переходном
процессе электропривода можно
интерпретировать как изменение суммарного
момента инерции электропривода
(6.150),тогда действие статического момента
(в рамках принятых допущений) в переходном
процессе электропривода можно
интерпретировать как изменение суммарного
момента инерции электропривода
 (6.151) и моменты количества движения(6.148)
и(6.149) записать таким образом:
(6.151) и моменты количества движения(6.148)
и(6.149) записать таким образом: ,
(6.152)
,
(6.152)
 ,
(6.153) Потери энергии в переходном процессе
при допущении
,
(6.153) Потери энергии в переходном процессе
при допущении
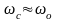 будут равны:
будут равны: ,
(6.154), Поскольку динамический момент
может быть положительным и отрицательным,
то потери энергии в переходном процессе
электропривода будут зависеть от
характера этого процесса. При разгоне
электропривода
,
(6.154), Поскольку динамический момент
может быть положительным и отрицательным,
то потери энергии в переходном процессе
электропривода будут зависеть от
характера этого процесса. При разгоне
электропривода
 и
и
 ,
что равносильно разгону вхолостую
электропривода с увеличенным моментом
инерции. Естественно, что потери энергии
при этом будут больше, чем при
,
что равносильно разгону вхолостую
электропривода с увеличенным моментом
инерции. Естественно, что потери энергии
при этом будут больше, чем при
 (Рис.6.16). Потери энергии при пуске
электропривода будут определяться
площадью треугольника ODG
для
(Рис.6.16). Потери энергии при пуске
электропривода будут определяться
площадью треугольника ODG
для
 и площадью ОАВ для
.
Можно видеть, что пл. ODG>пл.
ОАВ. При торможении электропривода
и площадью ОАВ для
.
Можно видеть, что пл. ODG>пл.
ОАВ. При торможении электропривода
 и
и
 ,
что эквивалентно торможению электропривода
вхолостую с уменьшенным моментом
инерции. Поэтому потери энергии при
торможении с
будут меньше, чем при торможении вхолостую
(Рис.6.17).
,
что эквивалентно торможению электропривода
вхолостую с уменьшенным моментом
инерции. Поэтому потери энергии при
торможении с
будут меньше, чем при торможении вхолостую
(Рис.6.17).
П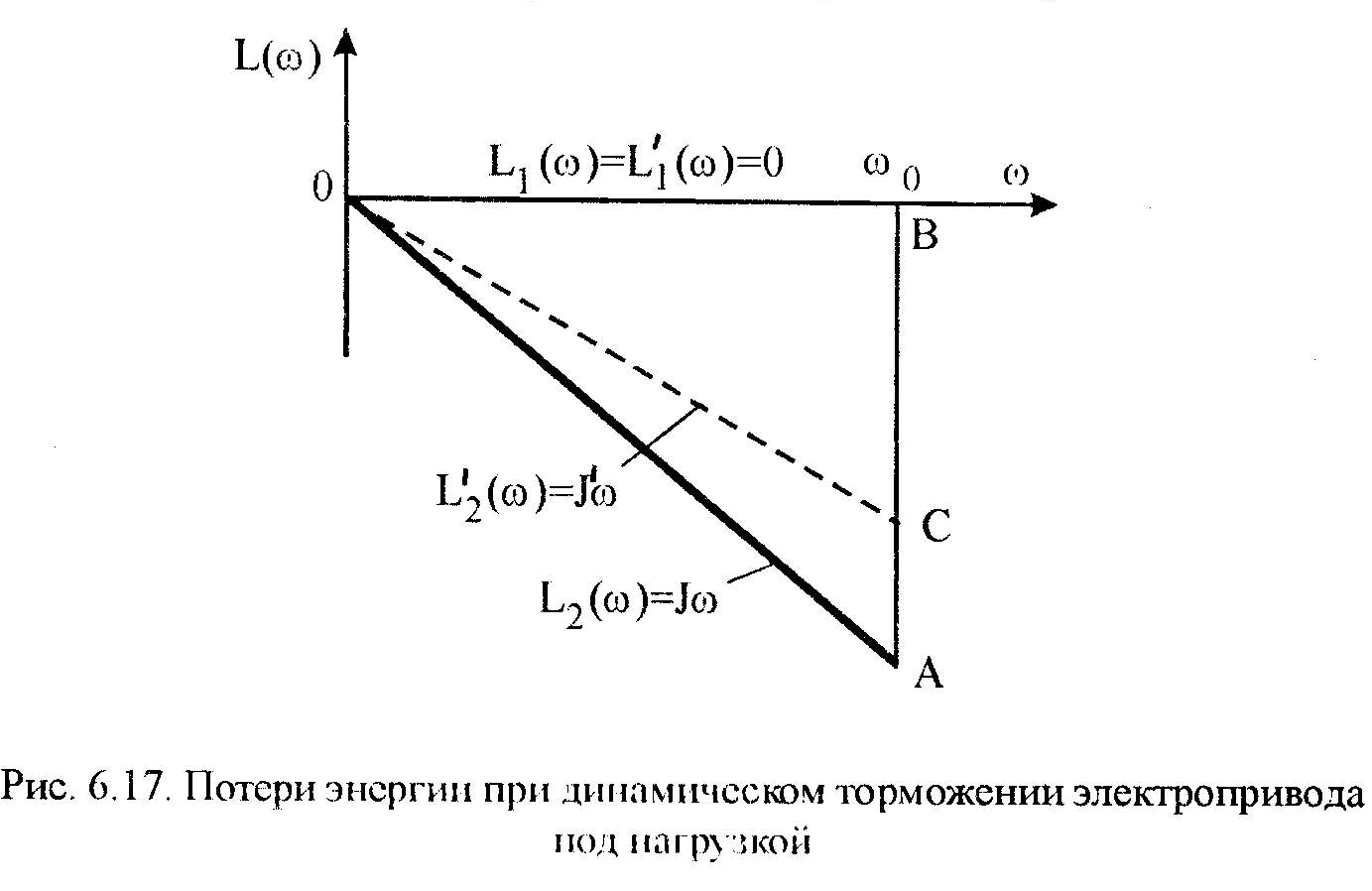 отери
энергии при динамическом торможении
электропривода равны площади треугольника
ОАВ при
и площади треугольника ОВС при
.
Из Рис.6.17 видно, что пл. ОВС< пл. ОАВ.
отери
энергии при динамическом торможении
электропривода равны площади треугольника
ОАВ при
и площади треугольника ОВС при
.
Из Рис.6.17 видно, что пл. ОВС< пл. ОАВ.
