1.7. Эл.Мех. Перех. Процессы при набросе и сбросе нагрузки эп

Положим, что до наброса нагрузки ЭП работал в установ. состоянии при условиях:

При этих условиях можно использовать уравнения (4.53) и (4.54).

После наброса нагрузки имеем

Цель исследования этого переходного процесса состоит в определении мах дин. падения скор., максимального электромагнитного момента и колебательности процесса.

Для определения экстремального значения скорости необходимо решить уравнение откуда находим

И Получим

Поскольку то

где _с – статическое падение скорости.

Теперь Экстремальное значение скорости (t_m) можно записать в виде

или

Время t_m достижения экстр. значений скор. удобнее найти из условия М_дин = 0, что соотв.

Важной хар-кой для взаимосвязанных ЭП является относительное восстановл. скорости

определяющее качество выпускаемой продукции. Чем меньше восстановление скор. при набросе нагрузки, тем меньше переменная деформация материала, проходящего через взаимосвязанные ЭП.

Колебательность переходного процесса оценивается логарифмическим декрементом затухания

Принимая Т_м = const в (4.40), можем найти отношение частот m_max , при котором достигается максимум частоты колебаний _р.max , решив уравнение

П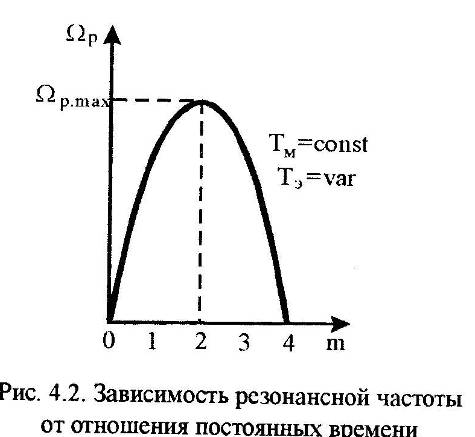 ри m = 0 (Т_э  ) и m  4 (Т_м  4Т_э) частота колебаний равна нулю (рис.4.2). При m =1 относительное восстановление скорости составляет =0,3. Следовательно, при m = 2, когда электромеханическая постоянная времени в два раза превышает электромагнитную, в электроприводе будут минимальными колебательность и относительное восстановление скорости. Для определения максимума электромагнитного момента в переходном процессе решаем уравнение

или из которого находим а затем

получим экстремальные значения электромагнитного момента

1.8. Механические переходные процессы электропривода с линейной механической характеристикой при линейном задании скорости идеального холостого хода.

И сходными уравн. в соотв. с рис. 4.1 являются:

где

– заданное угловое ускорение вала двигателя,

t₀ – время линейного изменения скорости идеального холостого хода ,

– начальное и конечное значения угловой скорости идеального холостого хода.

Д ля ДПТ для АД

эл.магн. момента

где

– заданное значение дин. момента ЭП.

для комплексно-сопряженных корней (m<4) имеет вид

– падение скорости, обусловленное заданным динамическим моментом . , – падение скор., обусловленное статическим моментом М_С.

решение дифференциального уравнения для электромагнитного момента

Если к валу ЭД приложен реактивный статический М, то в начале разгона ЭПбудет задержка движения на время

где на интервале 0≤t'≤t_З эл.магн. момент изменяется в соответствии с выражением а скорость двигателя равна нулю.

9) угловая скорость и электромагнитный момент определяются выражениями:

Если переходной процесс начинается с установившегося состояния, то выражения скорости (4.112) и электромагнитного момента (4.116) можно преобразовать к виду:

где φ₁ и φ₂ определяются соответственно (4.55) и (4.56).

Электромагнитный момент достигает экстремальных значений

(4.125) в момент времени

где n=1,2,3…

При этих условиях уравнения (4.120) и (4.121) могут быть представлены так:

(4.126)

(4.127)

где .

В случае, когда отношение постоянных времени m>4, можно получить уравн. скор.

(4.128)

и электромагнитного момента

(4.129)

для интервала линейно изменения скорости идеального холостого хода (0≤t≤t₀). Эти уравнения упрощаются для переходного процесса, начинающегося с установившегося состояния:

(4.130)

(4.131)

где φ₃ и φ₄ определяются соответственно формулами (4.67) и (4.68).

На интервале времени 0 ≤ t'' = t-t₀ ≤ 10T_Э переходной процесс описывается уравнениями скорости

(4.132)

и электромагнитного момента

(4.133)

(4.134)

и электромагнитного момента (рис. 4.7):

(4.135)

Если переходной процесс начинается с установившегося состояния, то

,

и (4.134), (4.135) приобретают вид

(4.136)

(4.137)