При переходе к пределам в (7.118) получаем

, (7.119)

где выражается через (7.47) и является функцией скорости ротора двигателя, которая, в свою очередь, зависит от времени t в пределах цикла.

Как частный случай, при независимой вентиляции ( ) имеем

, (7.120)

Предварительно выбранный двигатель, работая в расчетном режиме, не будет перегреваться, если

, (7.121)

К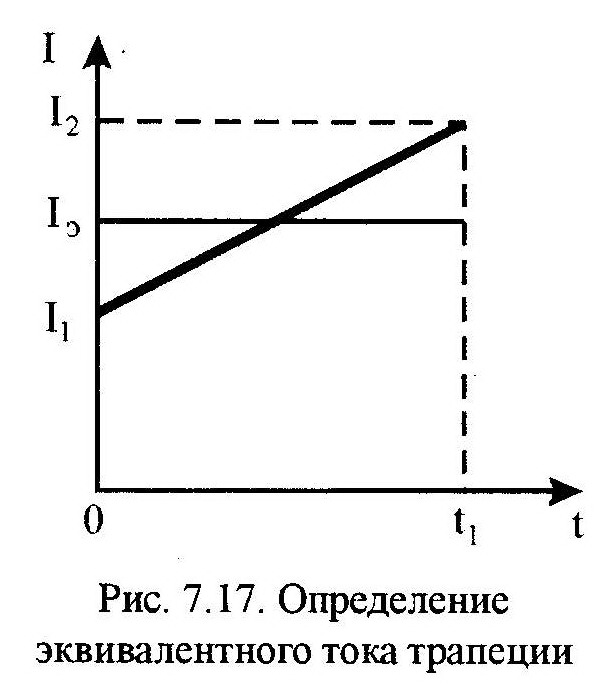 ривая тока I(t) обычно представляет сложную зависимость, которая только в отдельных случаях позволяет аналитически вычислить величину эквивалентного тока по (7.119) или (7.120). Чаще всего приходится осуществлять приближенное интегрирование кривой тока, разбивая ее на ряд элементарных фигур: трапеций, треугольников и прямоугольников. Наиболее общей элементарной фигурой является трапеция, поэтому найдем эквивалентный ток для трапеции (Рис.7.17).

На интервале времени t₁ ток двигателя изменяется по линейному закону

, (7.122)

где , (7.123)

Эквивалентное значение тока за время t₁ определяется выражением

, (7.124)

Продифференцировав (7.122), получим

, откуда , (7.125)

Теперь имеем новые пределы интегрирования: I₁ и I₂. Подставляем (7.125) в (7.124) и находим эквивалентный ток трапеции

, (7.126)

Для треугольника I₁=0, тогда , (7.127)

В прямоугольнике I₁=I₂, поэтому экв. ток прямоугольника , (7.128)

Заметим, что для прямоугольника эквивалентное, среднее и максимальное значение совпадают.

Таким образом, сложную кривую тока I(t), полученную в результате расчета переходных процессов за цикл, разбивают на ряд трапеций, треугольников и прямоугольников (Рис.7.18).

В свою очередь, трапеции и треугольники приводятся к эквивалентным прямоугольникам, как показано выше, так что эквивалентное значение тока всей диаграммы за цикл рассчитывается по формуле

, (7.129)

где - коэффициент охлаждения, соответствующий скорости на i-м участке токовой диаграммы.

Если для рассчитанного по (7.129) эквивалентного тока условие (7.121) соблюдается, то двигатель правильно выбран по нагреву. Затем выбранный двигатель проверяется на перегрузочную способность по току

, (7.130)

где I_max – максимальное значение тока на диаграмме I(t),

- допустимая перегрузочная способность двигателя по току.

Понятно, что метод эквивалентного тока можно применить, если имеется рассчитанная (или экспериментально снятая) токовая диаграмма за цикл работы электропривода.

Метод эквивалентного момента.

Метод экв. момента применим для ЭП с дв. постоянного тока при постоянном магн. потоке, а также для асинхронных двигателей, когда магнитный поток можно считать примерно постоянным. Его достоинство заключается в том, что определение эквивалентного момента не связано с параметрами двигателя, так как упрощенную нагрузочную диаграмму электропривода можно построить по данным исполнительного механизма. Поскольку для двигателя постоянного тока, работающего с неизменным магнитным потоком Ф, М=кФI=cI, (7.131)

где с=кФ=const, то , (7.132)

Подставив (7.132) в (7.129) , (7.129), получим выражение для расчета эквивалентного момента , (7.133)

Предварительно выбранный электродвигатель, работая в расчетном режиме, не будет перегреваться, если , (7.134)

Аналогично (7.119), можем записать общее выражение для эквивалентного момента

, (7.135), при , (7.136)

При этом приближенное интегрирование кривой M(t) осуществляется таким же образом, как и кривой тока.

Методом эквивалентного момента нельзя пользоваться при переменном магнитном потоке (двигатели постоянного тока последовательного и смешанного возбуждения, асинхронные короткозамкнутые двигатели, работающие в пуско-тормозных режимах).

После проверки двигателя по нагреву выполняют проверку его на перегрузочную способность: , (7.137)

где М_max – максимальное значение момента двигателя в цикле работы,

- допустимая перегрузочная способность двигателя по моменту.