Для ном. Реж. Можно записать равенство

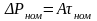, (7.104) где , (7.105)

- ном. мощ. и КПД ЭД.

На основании (7.102) – (7.104) формулируется метод средних потерь: если средние за цикл потери мощности не превышают номинальные потери, т.е. 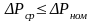, (7.106)

то средняя темп. перегрева не будет превышать допустимую, т.е. , Чтобы действительная темп. не отличалась значительно от ср., необходимо соблюдать условие , (7.108) , где Т_н – постоянная времени нагрева.

В общем случае ср. потери мощ. в ЭД за цикл рассчитывают по выражению:

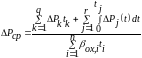, (7.109), где 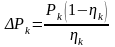, (7.110)

, (7.111) 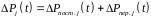, (7.112)

М_к, Р_к – момент и мощ. дв. на к-м участке с установившейся угловой скор. ; 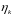- КПД ЭД при нагрузке М_к и скор. ; q – число участков в цикле с установившейся скор. дв.;r – число пуско-торм. участков в цикле, когда ; - коэфф, учитывающий охл. самовентил. дв. при и определяемый по (7.47);n – общее число участков в цикле: , (7.113); - потери мощ. в переходном процессе ЭД на j-м участке в момент времени t; t_i – продолжительность i-го участка цикла, на котором угловая скорость принимается постоянной или равной среднему значению.

Если в переходном процессе ЭП скор. дв. изменяется от нуля до установившегося значения, равного примерно ном., или наоборот, то коэфф. охл. рассчит. по ср. скорости

, (7.114) где определяется по (7.48) – см. табл.7.2.

КПД ЭД 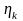при частичной загрузке в зависимости от способа регулирования скорости определяется в соответствии с положениями шестой главы.

Проверка нагрева ЭД методом средних потерь осуществляется по (7.106), где средние потери мощности вычисляются по (7.109).

Для пользования методом ср. потерь необходимо иметь зависимость КПД ЭД от коэфф. загрузки при данной скор., что в свою очередь требует расчета коэфф. постоянных потерь а. Кроме того, необходимо рассчитывать постоянные и переменные потери мощ. в переходных процессах ЭП, что связано с необходимостью знания всех параметров ЭД.

Несмотря на универсальность, метод ср. потерь имеет ограниченное применение.

Метод эквивалентного тока.

Метод основан на замене действительной переменной величины тока мнимой постоянной величиной тока, вызывающей такой же нагрев двигателя, что и реальный переменный ток. Потери мощности в двигателе представляют в виде суммы постоянных и переменных потерь, т.е.

, (7.115)где с – коэффициент, который учитывает число обмоток в двигателе, по которым протекает ток I,R – сопротивление одной обмотки.

При циклической нагрузке средние потери мощности выражаются (7.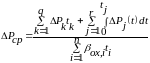109).

, (7.109)

Выразим потери на каждом участке графика нагрузки через постоянные и переменные, а переменные потери в средней мощности – через эквивалентный ток. В результате получим

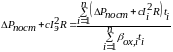, (7.116)

По определению постоянные потери не зависят от нагрузки, поэтому их можно сократить в левой и правой части равенства (7.116), приняв для них 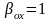. Тогда остается выражение

, (7.117)

Примем, что сопротивление R обмоток двигателя не зависит от тока (фактически такая зависимость имеется, так как сопротивление зависит от температуры, а температура зависит от тока). Это допущение позволяет сократить левую и правую часть выражения (7.117) на коэффициент cR. В результате получаем формулу для вычисления эквивалентного тока двигателя

, (7.118)