1.2. Формы теплообмена

Различают три формы теплообмена: теплопроводность, теплоотдачу и теплопередачу (рис. 37).

При теплопроводности передача теплоты внутри тел и сред осуществляется от одного слоя молекул к другому (рис. 37, а).

Теплоотдача заключается в процессе передачи теплоты от тела к среде (или наоборот) на их границе ( рис. 37, б).

Теплопередачей называют процесс передачи теплоты от одной среды к другой через твердую преграду (рис. 37, в).

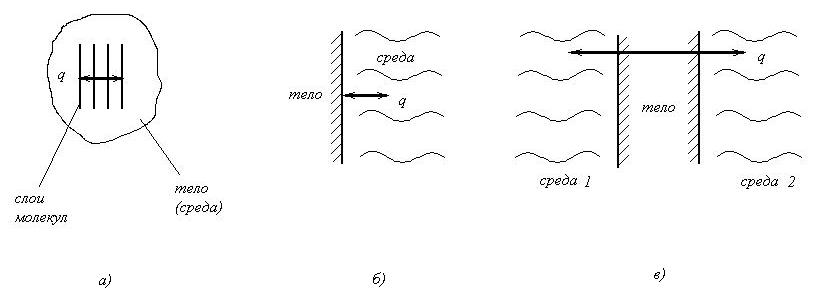
Рис. 37. Схемы, поясняющие формы теплообмена

1.3. Основные параметры теплообмена

К важнейшим параметрам теплообмена относятся:

- температура тела (среды) Т, измеряемая в “градусах Кельвина” [К];

- количество передаваемой теплоты Q (единицей ее измерения служит [Дж]);

- тепловой поток q, измеряемый в [Дж/с] = [Вт];

- плотность теплового потока q^*, измеряемая в [Вт/м²].

1.4. Закон теплопроводности (Фурье)

Математически закон теплопроводности выражается уравнением –

q^* = – λ·(dT/dn),

где q^* – плотность теплового потока; dT/dn – градиент температуры по направлению распространения потока, измеряемый в [К/м]; λ – коэффициент теплопроводности материала тела (среды), формально равный отношению q^*/(dT/dn) и измеряемый в [Вт/(К·м)]; n – координата, совпадающая с направлением распространения теплового потока.

Таким образом, закон Фурье утверждает, что плотность теплового потока в теле или среде пропорциональна коэффициенту теплопроводности вещества и градиенту температуры по направлению распространения теплового потока.

1.5. Закон конвективного теплообмена (Ньютона)

Для процесса теплоотдачи закон конвективного теплообмена имеет вид –

q^* = α·(Т_в – Т_ст),

где q^* – плотность теплового потока на границе “тело-среда” (“стенка-воздух”), см. рис. 37, б; Т_в – температура восстановления среды (воздуха) на границе с телом (стенкой), причем

Т_в = Т·[1 + r·(γ – 1)·M²/2];

здесь r – коэффициент потерь энергии, γ – коэффициент Пуассона среды, М – число Маха, Т – температура потока в произвольном сечении; Т_ст – температура тела (стенки), которая при практическом решении задач конвективного теплообмена, осуществляемого методом итераций, в первом приближении задается как ожидаемая; α – коэффициент теплоотдачи, измеряемый в [Вт/(К·м²)] и формально равный отношению q^*/(Т_в – Т_ст).

Для процесса теплопередачи справедливо равенство

q^* = К·(Т_в – Т_ст),

где коэффициент теплопередачи К = f (α₁, α₂, λ). Здесь α₁ и α₂ – коэффициенты теплоотдачи первой и второй сред соответственно, а λ – коэффициент теплопроводности материала преграды (см. рис. 37, в). Если она многослойная, то К = f (α₁, α₂, λ₁, λ₂, …).

Таким образом, согласно закону Ньютона плотность конвективного теплового потока пропорциональна разности температур среды и тела на их границе, а также коэффициенту теплоотдачи (теплопередачи).

1.6. Расчет процесса конвективного теплообмена

При решении задач конвективного теплообмена главное внимание уделяется определению коэффициента теплоотдачи α. Он, как правило, находится из экспериментально полученных критериальных уравнений теплообмена, характерных для исследуемого случая.

Например, для теплообмена между РТ (воздухом и продуктами сгорания топлива) и конструктивными элементами сопла ГТД, где Т_ст ≈ 0,8·Т_в, при вычислении α можно использовать соотношение

Nu = 0,0296·Re^0,8·Pr^1/3.

В этом уравнении критерий Нуссельта, величина безразмерная, составляет Nu = α∙d/λ_газа, где d – диаметр изучаемого сечения потока РТ (газа), и фактически представляет собой безразмерный эквивалент искомого коэффициента теплоотдачи α. Значение коэффициента теплопроводности РТ λ_газа выбирают из справочных таблиц. Критерий Рейнольдса Re, безразмерный эквивалент массовой скорости потока РТ, определяемой произведением w·ρ_газа, равен

Re = w·ρ_газа·d/η_газа,

где w, [м/с] – локальная скорость потока РТ в изучаемом сечении; ρ_газа, [кг/м³] – плотность РТ; η_газа, [Па/с] – динамическая вязкость потока РТ, выбираемая из справочных таблиц. Безразмерный комплекс физических параметров потока, критерий Прандтля, составляет –

Pr = c_p·η_газа/λ_газа,

где с_р – удельная изобарная теплоемкость РТ, [Дж/кг].

Таким образом, в рассматриваемом случае искомый коэффициент теплоотдачи α при известных параметрах потока РТ можно рассчитать по соотношению –

α = λ_газа·0,0296·Re^0,8·Pr^1/3/d.

Далее легко найти плотность теплового потока –

q^* = α·(Т_в – Т_ст).