
- •Заключение
- •Лекция 2. Основы математического моделирования взаимосвязи экономических переменных
- •Функциональная, статистическая и кореляционная зависимости
- •Параметры линейного однофакторного
- •Оценка величины погрешности линейного однофакторного уравнения.
- •Проблема автокорреляции остатков. Критерий Дарбина-Уотсона
- •Построение уравнения степенной регрессии
- •Двухфакторные и многофакторные уравнения регрессии
- •Тема 2. Оптимизационные методы математики в экономике Лекция 2. Оптимизационные модели Понятие оптимизационных задач и оптимизационных моделей
- •Оптимизационные задачи с линейной зависимостью между переменными
- •Геометрическая интерпретация оптимизационных задач линейного программирования.
- •Симплексный метод решения оптимизационных задач линейного программирования
- •Пример решения оптимизационных задач линейного программирования симплексным методом.
- •Двойственная задача линейного програмирования
- •Лекция 4. Нелинейное программирование. Метод множителей Лагранжа.
- •Метод множителей Лагранжа.
- •Лекция 5. Модели функционирования и оптимизации деятельности фирм
- •Резюме Основные параметры и характеристики пф:
- •Наиболее часто используемые производственные функции
- •Линейная функция.
- •Функция Алена.
- •Функция с линейной эластичностью замены факторов (функция les).
- •С полным взаимодополнением благ
- •Лекция 7. Модели экономического равновесия
- •Моделирование процесса достижения равновесия
- •Сходимость цены к равновесной во времени
- •«Нащупывание» равновесной цены по модели п.Самуэльсона
- •Лекция 8. Модели формирования и использования запасов Введение
- •Основные понятия и определения
- •Лекция 10. Моделирование экономического роста и стабилизации экономики.
- •Лекция 11. Модель делового цикла
Пример решения оптимизационных задач линейного программирования симплексным методом.
Пусть необходимо найти оптимальный план производства двух видов продукции (х1 и х2).
Исходные данные:
Вид продукции |
Норма расхода ресурса на единицу прибыли |
Прибыль на единицу изделия |
|
|
А |
В |
|
1 |
5 |
8 |
7 |
2 |
20 |
4 |
3 |
Объем ресурса |
20 |
36 |
|
Построим оптимизационную модель
![]()
![]() - ограничение по ресурсу А;
- ограничение по ресурсу А;
![]() - ограничение по ресурсу В.
- ограничение по ресурсу В.
Приведем задачу к приведенной канонической форме. Для этого достаточно ввести дополнительные переменные Х3 и Х4. В результате неравенства преобразуются в строгие равенства.
![]()
![]()
Построим исходную симплексную таблицу и найдем начальное базисное решение. Им будут дополнительные переменные, т. к. им соответствует единичная подматрица.
x3=20 и x4=36
Базисные переменные |
Свободные члены (план) |
x1 |
x2 |
x3 |
x4 |
x3 |
20 |
5 |
2 |
1 |
0 |
x4 |
36 |
8 |
4 |
0 |
1 |
Fj - Cj |
|
7 |
3 |
0 |
0 |
1- я итерация. Находим генеральный столбец и генеральную строку
max (7,3) = 7
![]()
Генеральный элемент равняется 5.
Базисные переменные |
Свободные члены (план) |
x1 |
x2 |
x3 |
x4 |
x1 |
4 |
1 |
0.4 |
0.2 |
0 |
x4 |
4 |
0 |
0.8 |
-1.6 |
1 |
Fj - Cj |
28 |
0 |
0.2 |
-1.4 |
0 |
2-я итерация. Найденное базисное решение не является оптимальным, т. к. cтрока оценок (Fj-Cj) содержит один положительный элемент. Находим генеральный столбец и генеральную строку:
max (0,0.2,-1.4,0) = 0.2
![]()
Базисные переменные |
Свободные члены (план) |
x1 |
x2 |
x3 |
x4 |
x1 |
2 |
1 |
0 |
1 |
-0.5 |
x2 |
5 |
0 |
1 |
-2 |
1.25 |
Fj - Cj |
29 |
0 |
0 |
-1 |
-0.25 |
Найденное решение оптимально, так как все специальные оценки целевой функции Fj - Cj равны нулю или отрицательны. F(x)=29 x1=2; x2=5.
Примечания к симплекс-методу.
Если в ведущем столбике нет ни одного строго положительного элемента, то задача не имеет оптимального решения, а целевая функция неограничена снизу (в задаче на минимум) или неограничена сверху (в задаче на максимум).
Несовместимость системы ограничений (в канонической форме) обнаруживается при построении начального д.б.р. (оно не существует).
Если в последней (оптимальной) таблице оценка какой-либо небазисной переменной (число в нулевой строке) равна нулю, то задача имеет бесконечное множество оптимальных решений.
Симплекс-метод за конечное число итераций либо приводит к оптимальному решению, либо устанавливает неразрешимость задачи (см. пп. 1,2,3).
На каждой итерации симплекс-метод сохраняет допустимость базисного решения, т.е. неотрицательность элементов нулевого столбика - следствие правила выбора ведущей строки.
На каждой итерации целевая функция убывает (в задаче на минимум) или возрастаем (в задаче на максимум); это свойство нарушается только в случае зацикливания (см. примечания 11,12).
В качестве ведущего столбика можно выбирать любой столбик с положительной оценкой (в задаче на минимум), однако максимальность оценки ведущего столбика ведет к сокращению числа итераций (целевая функция быстро убывает).
Слабые переменные со знаком "+" (вводимые для преобразования неравенств вида "
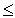 ")
можно использовать в качестве базисных
переменных, а слабые переменные со
знаком "-" (вводимые для преобразования
неравенств вида "
")
можно использовать в качестве базисных
переменных, а слабые переменные со
знаком "-" (вводимые для преобразования
неравенств вида "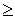 ") - нет.
") - нет.
Структуру симплекс-таблицы можно упростить, если на каждой итерации исключать из таблицы столбики для базисных переменных. При этом сокращается объем вычислений.
При решении симплекс-методом задачи на максимум изменяется только правило выбора ведущей строки (столбик с минимальной отрицательной оценкой) и критерий оптимальности (отсутствие в нулевой строке отрицательных оценок).
Д.б.р., в котором одна или несколько базисных переменных равны нулю, называется вырожденным д.б.р. Появление такого д.б.р. в процессе решения может привести к зацикливанию, т.е. к повторному вхождению переменной в базис (геометрически: возвращение к предыдущей вершине многогранника). Предвестником зацикливания является неоднозначное определение ведущей строки.
Для выхода из зацикливания: в критерии определения ведущей строки вместо элементов 0-го столбика применяют элементы 1-го столбика; если и здесь ведущая строка неоднозначна, то применяют элементы 2-го столбика и т.д., пока ведущая строка не будет определена однозначно.
