Резюме Основные параметры и характеристики пф:

1. полная производительность факторов производства;

2. средняя производительность факторов производства и ресурсоемкость продукции;

3. предельная производительность фактора производства;

4. предельная норма замещения фактора производства;

5. частный коэффициент эластичности производственной функции;

6. суммарная эластичность по масштабу производства;

7. эластичность замещения факторов производства;

8. изокванты производственной функции.

Наиболее часто используемые производственные функции

1. Линейная функция.

У данной функции предельные производительности факторов постоянны, эластичность замены факторов – бесконечна. Функция может использоваться в тех случаях, когда вклад каждого ресурса независим, например: производственная система состоит из отдельных производственных единиц, каждая из которых использует свой собственный производственный ресурс, подходящий только для этого производства.

2. Функция Алена.

Такая функция предназначена для описания производственных процессов, в которых чрезмерный рост любого из факторов оказывает отрицательное воздействие на объем выпуска. Обычно такая функция используется для описания мелкомасштабных систем с ограниченными возможностями переработки ресурсов.

3. Функция с линейной эластичностью замены факторов (функция les).

Функция LES применяется для описания производственных процессов, у которых (в отличие от описываемых функцией CES) возможность замещения вовлекаемых факторов существенно зависит от их пропорций, причем при низком уровне отношений близка к единице, а с ростом отношения - неограниченно возрастает. Такая ситуация возможна, например, если рост ресурсов x₁ связан с общим расширением производства, появлением множественных технологических процессов с широкими возможностями комбинирования.

4. Функция Солоу.

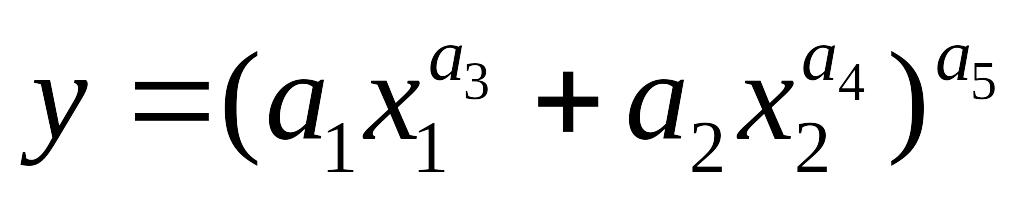
Характеризуется тем, что величина процентного изменения предельной нормы замещения факторов, вызванного увеличением любого фактора на один процент, не зависит от начального уровня фактора. Эта функция может использоваться, когда влияние на объем выпуска увеличения каждого из факторов проявляется различным образом.

5. Ограниченная функция CES.

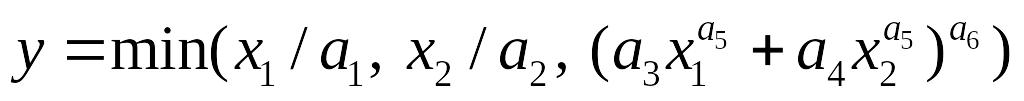
Функция предназначена для выражения двухрежимного производственного процесса, в котором один из режимов характеризуется отсутствием заменяемости факторов, другой – ненулевой постоянной величиной эластичности замены. При этом переход от одного режима к другому осуществляется в зависимости от уровня лимитирующего первый режим фактора.

6. Многорежимная функция.

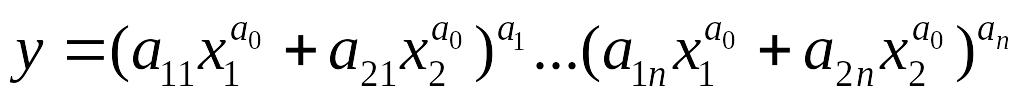
Одна из наиболее общих форм производственных функций. Она используется при описании процессов, в которых уровень отдачи каждой новой единицы ресурса скачкообразно меняется в зависимости от соотношения факторов. Функцию целесообразно применять при наличии информации о числе режимов n и о ширине "переходной" области между режимами (чем выше a₀, тем более отчетливо выделяются режимы).

7. Функция линейного программирования.

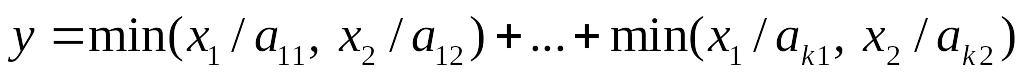
Функцию имеет смысл использовать в тех случаях, когда выпуск продукции является результатом одновременного функционирования k-фиксированных технологий, использующих одни и те же ресурсы.

8. Описание технического прогресса.

При построении производственных функций научно-технический прогресс может быть учтен с помощью множителя , где параметр  характеризует темп прироста выпуска под влиянием научно-технического прогресса:

Данная производственная функция является примером динамической производственной функции. Она включает нейтральный, то есть не материализованный в одном из факторов технический прогресс. Другим подходом является выражением технического прогресса от прироста основных фондов в году t или от инвестиций в научные исследования, что эконометрически предпочтительней. В более сложных случаях технический прогресс может воздействовать непосредственно на производительность труда или капиталоотдачу:

где K – основные фонды; L – трудовые ресурсы; A(t) и B(t) – заданные функции времени, причем A(t) описывает повышение эффективности использования основных фондов; B(t) – трудовых ресурсов.

Оптимизация издержек производства и объема выпуска продукции

Задача минимизации издержек производства

Для нахождения оптимальных решений производителю не достаточно знания производственных функций, которые содержат лишь технологическую информацию, так как отсутствует информация о цене продукции и ценах на ресурсы. Пусть q₁, q₂, …..q_n – цены соответственно ресурсов x₁, x₂, ….., x_n. Тогда издержки составят величину

Задача минимизации издержек производства следующая: для заданного объема выпуска продукции y₀ найти такое сочетание ресурсов, чтобы их стоимость (затраты) была минимальной. В математической форме

при условиях

Для n=2 решение задачи изображено на рис.

Геометрически формулировка задачи следующая: задана изокванта и нужно среди линий уровня, называемых изокостами (параллельных прямых) функции , найти касательную к данной изокванте. Точка касания x* и есть оптимальное решение.

Задача решается методом множителей Лагранжа. Функция Лагранжа имеет вид:

Приравнивая к 0 частные производные функции Лагранжа, получаем систему уравнений

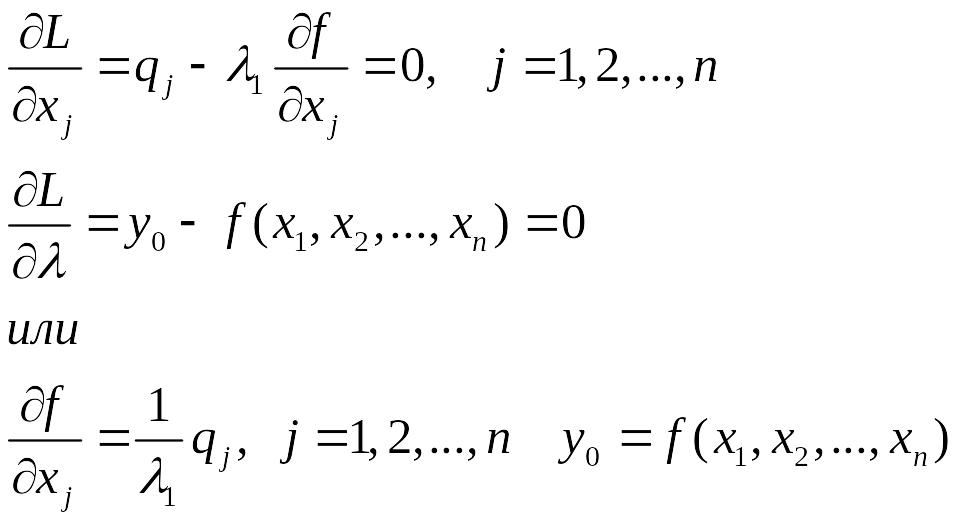
Таким образом, в точке минимума будем иметь:

1. предельные производительности ресурсов пропорциональны их ценам

2. отношение предельных производительностей ресурсов равно отношению их цен

3. отношение предельных производительностей ресурсов к их ценам равны между собой

Полученные соотношения составляют основу теории предельной производительности факторов производства как теории стоимости, а именно: цены ресурсов пропорциональны предельным производительностям ресурсов, в частности для труда имеем, что он оценивается в соответствии со своей предельной производительностью.

Дадим интерпретацию множителя Лагранжа.

В точке минимума

следовательно

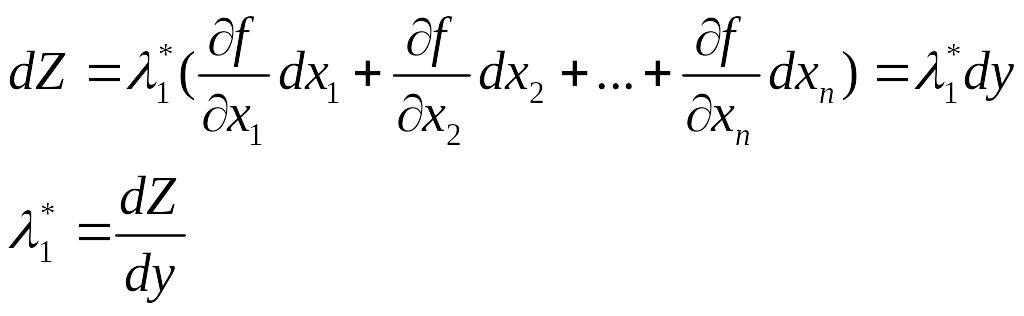
т.е. ₁^* есть общие предельные издержки на единицу дополнительной продукции.

Функция издержек

Мы нашли оптимальное сочетание ресурсов x₁*, x₂*, … x_n*, для обеспечения данного объема выпуска продукции y₀ при фиксированных ценах на эти ресурсы. Меняя y₀ в данной задаче, получим зависимость оптимального объема ресурсов от объема выпуска продукции x*=x*(y). Такую вектор-функцию называют функцией производственных затрат ресурсов, а сами издержки

называют функцией издержек, которая обозначается C(y)=Z_min(y).

однако эта зависимость от объема выпуска (у) для разных видов издержек различна. А именно имеют место :

а) постоянные расходы C₀, которые практически не зависят от y, в т.ч. оплата административного персонала, аренда и содержание зданий и помещений, амортизационные отчисления, проценты за кредит, услуги связи и т.п.:

б) пропорциональные объему выпуска (линейные) затраты C₁, сюда входят материальные затраты C_m, оплата труда производственного персонала (часть C_l) , расходы по содержанию действующего оборудования и машин (часть C_k) и т.п.

C₁ = ay,

где а - обобщенный показатель затрат указанных видов в расчете на одно изделие

в) “сверхпропорциональные” (нелинейные) затраты С₂, в составе которых выступают приобретение новых машин и технологий т.е. затраты типа С_r), оплата сверхурочного труда и т.п. Для математического описания этого вида затрат обычно используется степенная зависимость

С₂ = by^h (h > 1).

Задача максимизации объема выпуска продукции

Задача максимизации объема производства состоит в том, чтобы определить максимальный объем выпуска продукции при заданных затратах ресурсов.

Математическая формулировка:

Геометрически для n=2 это означает, что задана изокоста с уравнением q₁x₁+q₂x₂=C и нужно найти ту изокванту производственной функции, которая касается этой изокосты. Точка касания x₁*, x₂* и есть оптимальное решение, а максимальный объем выпуска продукции y*.

Функция Лагранжа для этой задачи имеет вид:

Условия оптимальности запишутся:

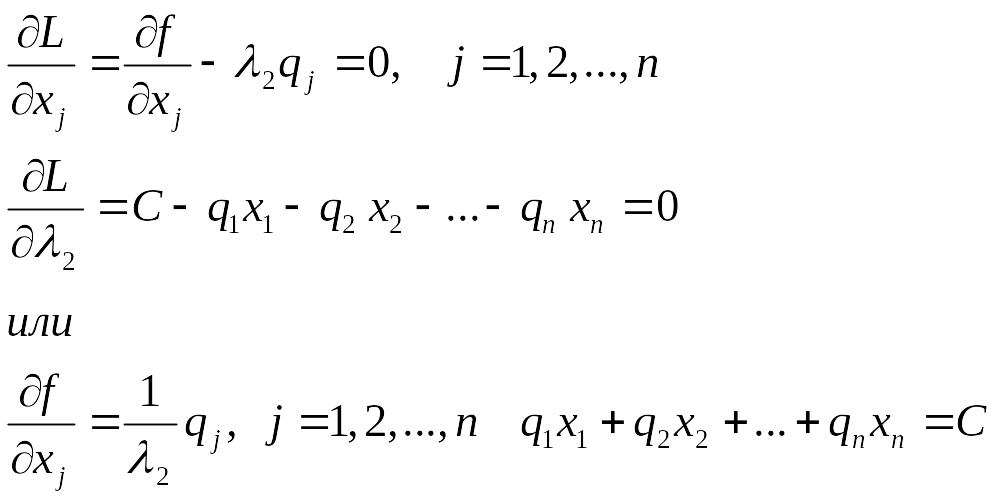
В точке максимума x* будут иметь место соотношения, аналогичные соответственным соотношениям в задаче минимизации издержек.

Дадим интерпретацию множителя Лагранжа.

В точке максимума

следовательно

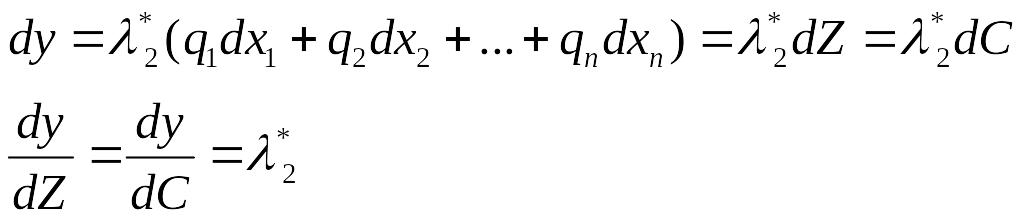
Таким образом, ₂*выражает дополнительный выпуск продукции в расчете на единицу общих затрат, т.е. он выражает общую предельную производительность ресурсов. ₁* и ₂* для рассмотренных задач по смыслу взаимообратные. Поэтому эти задачи называют взаимными задачами для производителя.

Лекция 6. Математические модели потребительского поведения и спроса

В основе моделей потребительского поведения и спроса лежат модели распределения доходов и теория полезности. Рассмотрим вначале модели распределения доходов.

Модели распределения доходов

В основе построения моделей личного потребления лежит принцип распределения потребителей по группам, для формирования которых используются как данные о социальном положении семей, так и сведения об их доходах. В соответствии с этим подходом все множество потребителей, т.е. население страны или региона, рассматривается как совокупность нескольких групп семей, каждая их которых характеризуется определенным уровнем дохода и примерно одинаковым социальным статусом (служащие, рабочие, крестьяне и т.п.). При этом считается, что каждая такая группа обладает некоторой общностью в выборе и предпочтении тех или иных потребительских благ. При разбиении потребителей на группы по различным уровням дохода обычно используют модели распределения доходов различных типов.

Для характеристики равномерности распределения доходов в обществе часто используется т.н. кривая Лоренца. Она строится следующим образом: все множество потребителей данной страны или региона разбивается на некоторое количество групп, обычно равных по численности, но различных по доходам. Затем подсчитывается какую долю национального дохода получает каждая такая группа, причем счет ведется начиная с группы с наименьшим доходом в сторону его увеличения.

Далее на диаграмме (рис. 1) наносятся точки, соответствующие вычисленным долям в процентах. Очевидно, что совершенно равномерному распределению дохода отвечает прямая линия (биссектриса угла на диаграмме), если же распределение неравномерное, то возникает кривая линия, причем ее кривизна и отклонение от биссектрисы будет тем более, чем менее равномерным оказывается распределение доходов.

На рис. 1 представлены три случая распределения доходов в случае, когда население разделено на 5 равных по численности (по 20% каждая) групп. Прямая А соответствует равномерному распределению, кривая В иллюстрирует следующее распределение доходов:

Рис. 1. Кривые Лоренца

1 группа имеет 15% дохода, 2 группа - 18%, 3 группа - 20%, 4 группа - 22% и 5 группа - 25%.

Кривая С отвечает еще более неравномерному распределению доходов.

1 группа получает 10% , 2 группа 15%, 3 группа 18%, 4 группа 20%, 5 группа 37%.

Модель распределения доходов, принадлежащая В.Парето, также предназначена для анализа характера неравномерности доходов в обществе. Она строится следующим образом:

Обозначим через I_m - наименьший доход, который может получать семья в данном обществе. Тогда для характеристики относительного числа семей (в процентах) N(I), получающих доход не менее, чем I, может быть использовано соотношение:

которое является модификацией формулы В. Парето.

Исследования, проведенные в различных странах и в разные периоды времени дают основание полагать, что указанное соотношение вполне применимо и в том случае, когда речь идет о доходах от недвижимости и капитальных вложений. При этом показатель  обычно находится в интервале от 1.2 до 2. Очевидно, что меньшие значения  соответствуют более равномерному распределению доходов в обществе, а высокое значение  свидетельствует о резкой дифференциации доходов. В литературе можно встретить мнение о том, что при  = 1,5 имеет место сравнительно справедливое распределение доходов (рис. 2)

Рис. 2. Модель распределения доходов В. Парето

Здесь линия АВ соответствует распределению дохода с  = 1.5, линии АС и АD значениям  = 2 и  =1,2.

Разбиение на доходные группы в случае  =1.5 может быть выполнено следующим образом:

первая группа, имеет доход от I_m до 2I_m, состоит из 65% потребителей

вторая группа, имеет доход от 2I_m до 3I_m , включает 17% потребителей,

третья группа с доходом 3I_m до 4I_m , в нее входят 7% потребителей и т.д. (рис. 3).

Рис. 3. Доходные группы населения при =1.5

Результаты исследований, проведенных в обществах, где основным источником доходов является заработная плата, показывает, что эти доходы распределяются скорее по нормальной кривой, впрочем не совсем симметричной и с урезанными концами (рис. 4).

Рис. 4. Нормальная кривая распределения доходов

Такой вид кривой объясняется наличием как нижнего, так и верхнего предела заработков; причем возможность получения высокой заработной платы ограничена вследствие воздействия многих факторов, совокупное влияние которых и приводит к квазинормальной кривой распределения доходов.

Разбиение на доходные группы в этом случае имеет вид, представленный на рис. 5

Рис. 5. Квазинормальное распределение доходов

Выбор конкретной модели распределения доходов, а следовательно и способ формирования доходных групп определяется в результате анализа данных о доходах потребителей в рассматриваемом обществе или регионе.

В дальнейшем изложении основ теории потребления мы будем исходить из того, что указанное формирование групп произведено и множество потребителей представлено как совокупность m групп с номерами i=1,...,m.

При этом, как уже отмечалось выше, предполагается, что члены группы достаточно схожи в определении своих предпочтений, и, следовательно, вся группа может рассматриваться как единый потребитель в вопросах формирования спроса на товары и услуги, выступающие на потребительском рынке.

Количественный подход к анализу полезности и спроса

Порядковый подход к анализу полезности является наиболее распространенным. От потребителя не требуется, чтобы он умел соизмерять блага в каких-то искусственных единицах измерения. Достаточно, чтобы потребитель был способен упорядочить все возможные товарные наборы по их «предпочтительности». В порядковой теории полезности понятие «полезность» означает не что иное как порядок предпочтения. Утверждение: «Набор А предпочтительнее для данного потребителя, чем набор В», - тоже самое, что и утверждение: «Набор А полезнее для данного потребителя, чем набор В». Вопрос на сколько единиц полезнее набор А, чем набор В не ставится. Потребитель выбирает предпочтительный набор товаров из всех доступных для него.

Рассмотрим наборы только из двух товаров  и . (Товары  и  можно рассматривать как комбинированные товары).

Отношения предпочтения, характерные для каждого индивида, отражают посредством кривой безразличия (рис.6).

Кривая безразличия отражает множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Наборы А и В с точки зрения данного потребления равноценны и лежат на одной и той же кривой безразличия. Для нашего потребителя любой набор, лежащий на кривой II, предпочтительнее любого набора, лежащего на кривой I и т. д.

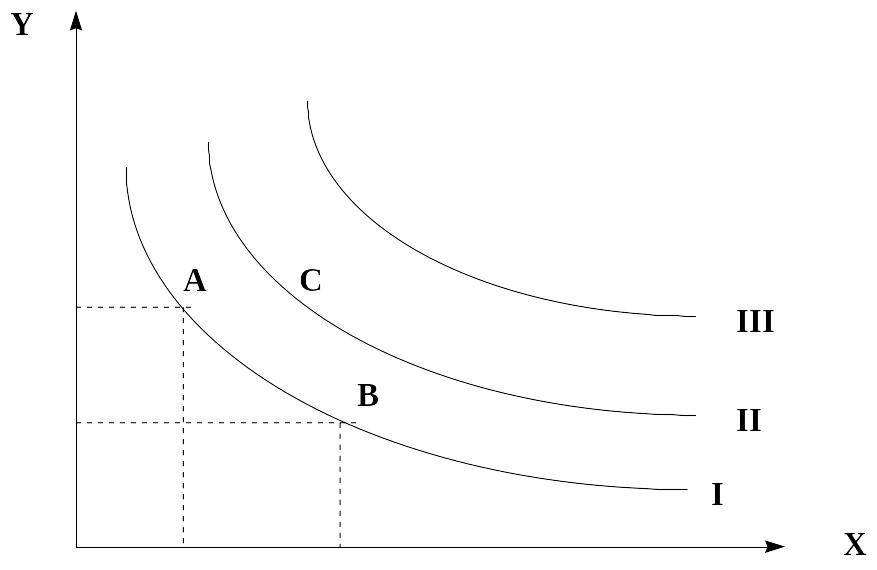
Рис. 6. Кривые безразличия

В зависимости от функций полезности различают следующие типы кривых безразличия:

1). Функция полезности с полным взаимозамещением благ (чай и кофе) имеет вид:

,

где a,b - параметры;U - полезность; X,Y - товары.

Из функции полезности можно найти Y

и построить кривые безразличия линейного типа (рис. 7).

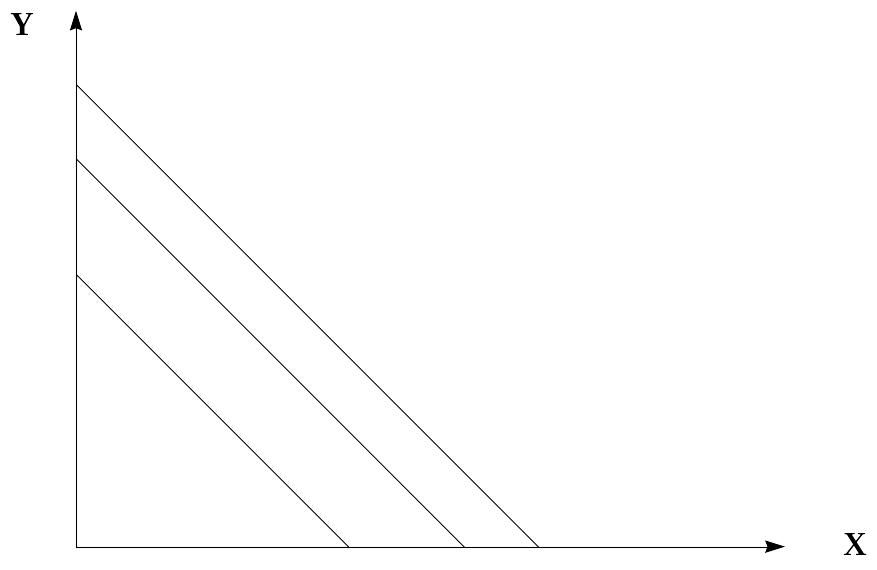
Рис. 7. Кривые безразличия линейного типа

2).Неоклассическая функция полезности имеет вид:

, где a+b  1

Чтобы построить кривые безразличия необходимо найти Y:

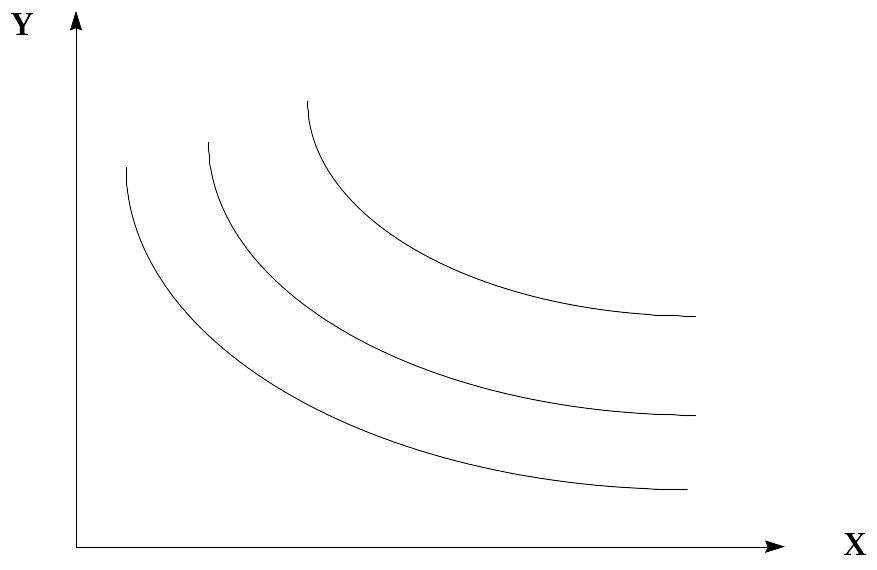
Рис. 8. Кривые безразличия неоклассического типа

3) Функции с полным взаимодополнением благ (при увеличении спроса на одно из двух благ растет спрос и на второе благо, например, сахар и чай, бензин и моторное масло) имеют кривые безразличия в виде точки на пересечении двух прямых. Избыток одного блага не имеет значения. Полезность достигается лишь при определенной комбинации обеих благ.

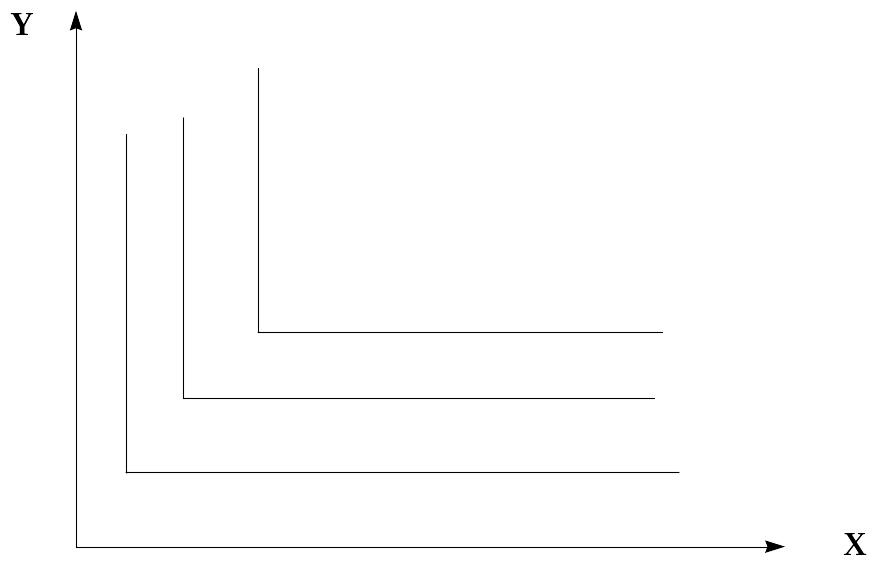
Рис. 9. Кривые безразличия функций