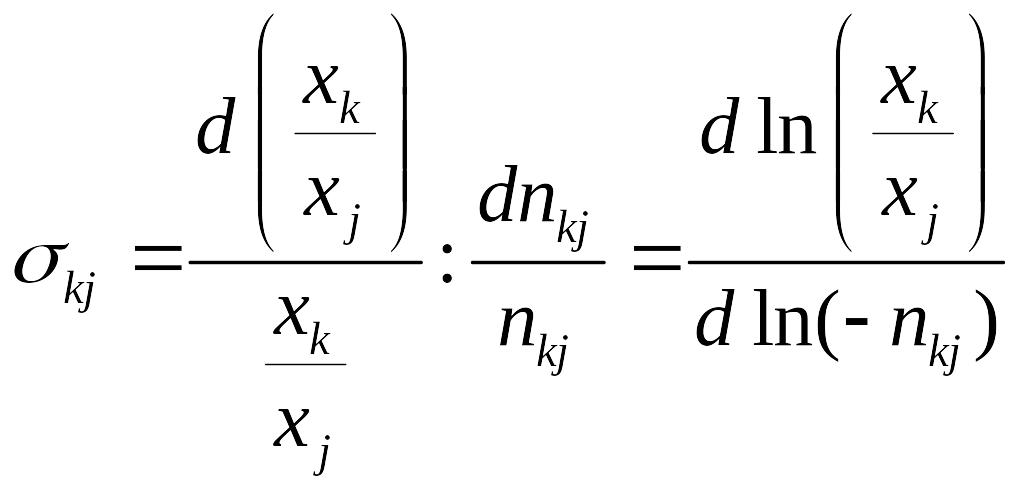Лекция 5. Модели функционирования и оптимизации деятельности фирм

ПРОИЗВОДСТВО

Изокванты и предельная производительность

Хотя предмет микроэкономической теории производства иной — проблемы производственной деятельности предприятий, ход рассуждений здесь очень близок к теории потребления. Функциям полезности и кривым безразличия, описывающим потребление, соответствуют производственные функции и изокванты, описывающие производство. Более того, свойства этих функций и формы кривых одинаковы.

Начнем с того, что определим производственную деятельность как процесс, в ходе которого предприятия затрачивают различные ресурсы — вещественные блага и услуги (факторы производства), например труд и капитальное оборудование, и в результате выпускают разнообразную, ориентированную на рынок продукцию (продукты производства). Отправной точкой микроэкономической теории производства является идея о том, что технологически эффективная производственная деятельность предприятия, в ходе которой для выпуска, например, одного вида продукции Y затрачивается два вида ресурсов X₁ , X₂, может быть описана с помощью производственной функции Y=f(X₁ , X₂) . Если для фиксированного выпуска Y изобразить на плоскости (X₁ , X₂) все возможные сочетания необходимых ресурсов (X₁ , X₂), мы получим кривую, называемую изоквантой. Так же как и для функций полезности и кривых безразличия, можно выделить по крайней мере три типа производственных функций и изоквант.

1. Функции с полным взаимозамещением ресурсов, например,

2. Неоклассическая производственная функция, например,

3. Функции с полным взаимодополнением ресурсов, например,

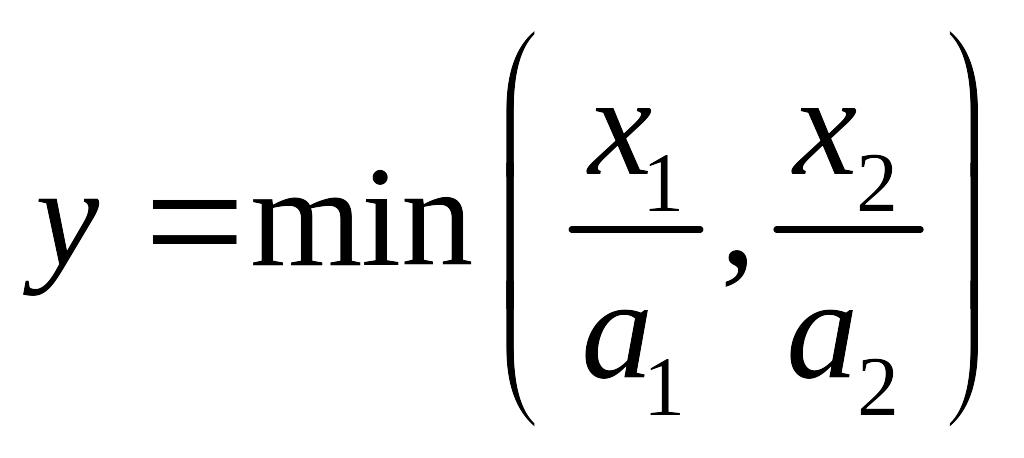
Свойства производственных функций

При анализе производственных функций закладываются следующие предположения о свойствах таких функций:

Математические предположения:

1. Производственная функция задана при всех неотрицательных значениях своих аргументов

2. ПФ является непрерывной или нужное число раз дифференцируемой функцией своих аргументов

Экономические предположения:

2. Производство невозможно при отсутствии хотя бы одного ресурса

Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Полное его отсутствие не может быть компенсировано другими ресурсами.

2. При увеличении затрат производственных ресурсов выпуск продукции не уменьшается.

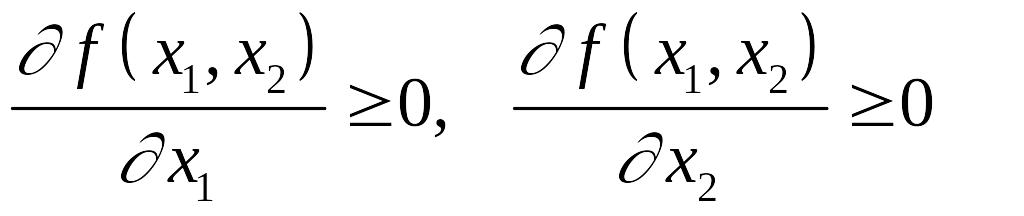
Это означает, что предельные эффективности ресурсов положительны.

Это условие выполняется не всегда. Например, при возрастании количества удобрений, приходящихся на единицу площади, производство зерна сначала растет, а затем начинает снижаться. Поэтому для производственных функций, не удовлетворяющих этому соотношению, вводится понятие экономической области. Использование ресурсов в сочетаниях, не попадающих в экономическую область, бессмысленно с экономической точки зрения.

4. По мере увеличения количества одного ресурса при постоянных количествах других предельная эффективность использования этого ресурса не возрастает.

Заметим, что только серьезные достижения научно-технического прогресса могут снять эту проблему.

С чем связано снижение предельного продукта? Представим себе предприятие, хорошо оснащенное различным оборудованием, имеющее достаточную площадь для осуществления производственного процесса, обеспеченное сырьем и различными материалами, но располагающее малым числом рабочих. На фоне остальных ресурсов рабочая сила является своего рода узким местом, и, надо полагать, дополнительный работник будет использован весьма рационально. Соответственно прирост продукции может быть значительным. Если же при сохранении прежних уровней всех прочих ресурсов число рабочих будет большим, труд дополнительного работника не будет уже столь хорошо обеспечен инструментом, механизмами, ему, возможно, будет мало места для работы и т. д. В этих условиях привлечение дополнительного работника не вызовет большого прироста выпуска продукции. Чем больше работников, тем меньше прирост выпуска продукции, обусловленный привлечением дополнительного работника.

4. Если  - масштаб производства, то можно ожидать увеличения вследствие роста ресурсов, т.е.

или .

Соотношения (1)-(4) – основные гипотезы о свойствах производственных функций любого производства.

Характеристики производственных функций

ПРОИЗВОДИТЕЛЬНОСТЬ

В микроэкономике с помощью понятия производительности анализируется эффективность использования факторов производства. Различают три вида производительности фактора: полная производительность, средняя производительность и предельная производительность.

Рассмотрим случай функции двух переменных y=f(K,L), где K – капитальные ресурсы, L – трудовые.

Полная производительность фактора производства

Функция показывающая как изменяется объем производства при изменении одного из факторов

y=f(K,L)_L=const y=f(K,L)_K=const

Средняя производительность фактора производства

А=y/x_j j=1,2 – объем выпускаемой продукции на единицу используемого объема j-ого фактора (Если x_j – труд – получаем производительность труда; если основные фонды – фондоотдачу)

Ресурсоемкость – величина обратная средней производительности –

r_j = x_j /y

В частности получаем следующие известные показатели: трудоемкость, фондоемкость, материалоемкость, энергоемкость, если в качестве ресурса соответственно выступают труд, фонды, материалы, энергия.

Предельная производительность фактора производства

MR=( ) – вклад единицы фактора производства в прирост продукции

Предельная норма замещения (MRS) ресурсов

— это предельное отношение замены первого ресурса вторым, — dX₂/dX₁, в ситуации, когда при постоянном выпуске Y сокращение затрат первого ресурса на—dX₁ компенсируется ростом затрат второго ресурса на dX₂. Подобно теории потребления, это отношение равно отношению частных производных производственной функции, т. е. предельных производительностей ресурсов:

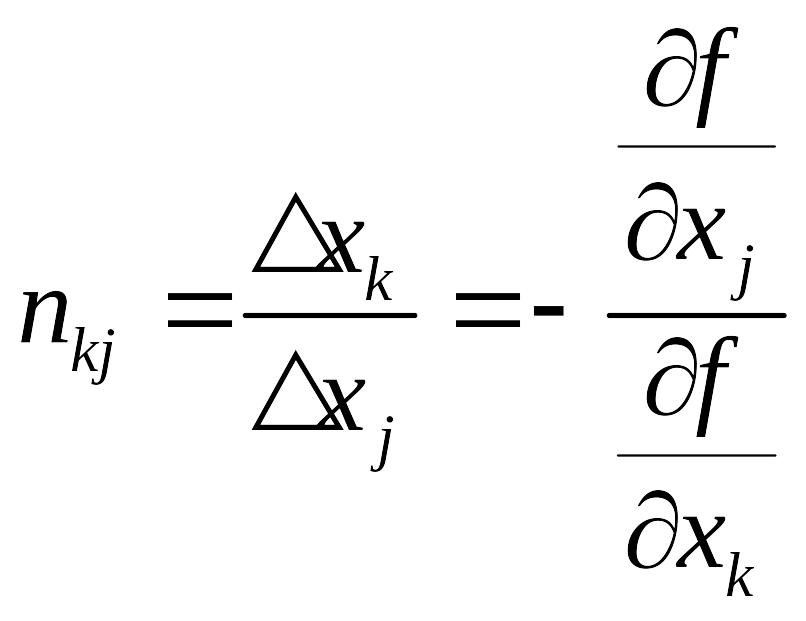
Изокванты неоклассической производственной функции, также как и кривые безразличия, являются гладкими вогнутыми кривыми, а предельная норма замещения ресурсов MRS постепенно убывает.

Коэффициенты эластичности

Частным коэффициентом эластичности ПФ по j-ому ресурсу называют отношение предельной производительности этого ресурса к его средней производительности

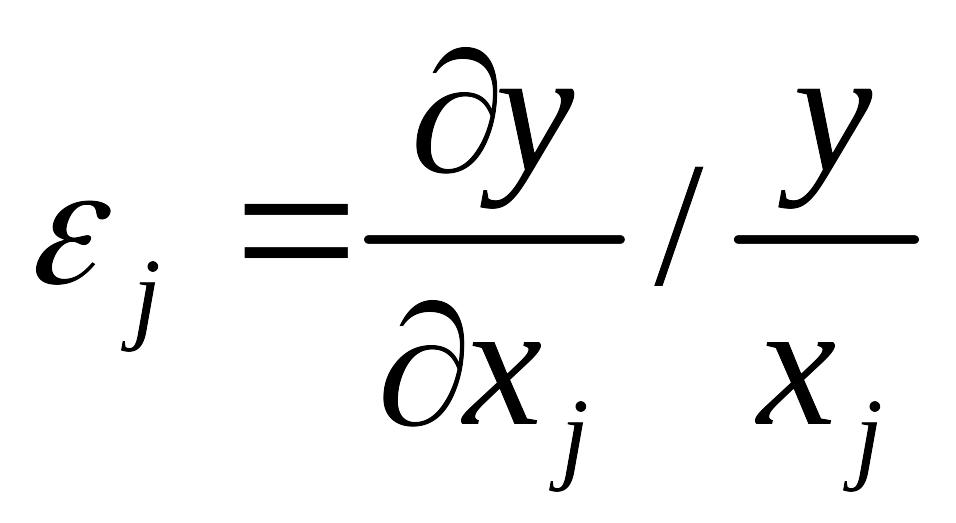
темп роста выпуска продукции/ рост фактора производства

Суммарная эластичность – сумма частных коэффициентов эластичности

Эластичность замещения ресурсов – показывает, на сколько процентов должно измениться отношение количества k-ого ресурса к количеству j-ого при движении вдоль изокванты, чтобы предельная норма замещения n_kj изменилась на один процент