Метод множителей Лагранжа.

Прежде всего, определим понятие условного экстремума функции.

Условным экстремумом функции называется максимум или минимум этой функции, достигнутый при условии, что x₁ и x₂ удовлетворяют дополнительному условию (уравнению связи)

Рассмотрим пример. Функция определяет параболоид вращения. Ее безусловный минимум равен 0 и достигается в начале координат. Присоединим ограничение . Графически этому уравнению на плоскости x₁Ox₂ отвечает прямая АВ. Теперь задача состоит в том, чтобы на линии найти точку М, в которой значение данной функции является наименьшим. Эта точка и будет точкой условного минимума. В данном случае такой точкой будет М(1/2, 1/2) и ей соответствует f_min=1/2.

Условный экстремум функции при наличии дополнительного ограничения находят с помощью так называемой функции Лагранжа.

, (1)

где  - неотрицательный постоянный множитель (множитель Лагранжа), безусловный экстремум которой совпадает с условным экстремумом данной функции . Объясняется это тем, что для точек x₁ и x₂ удовлетворяющих условию , второе слагаемое в (1) обращается в 0, и тогда L=f. Для остальных же точек Lf. Отсюда и следует, что задача на определение условного экстремума функции f может быть заменена нахождением обычного экстремума функции L, ибо в области допустимых решений функцию f можно заменить функцией Лагранжа.

Необходимое условие экстремума сводится к существованию решения системы трех уравнений

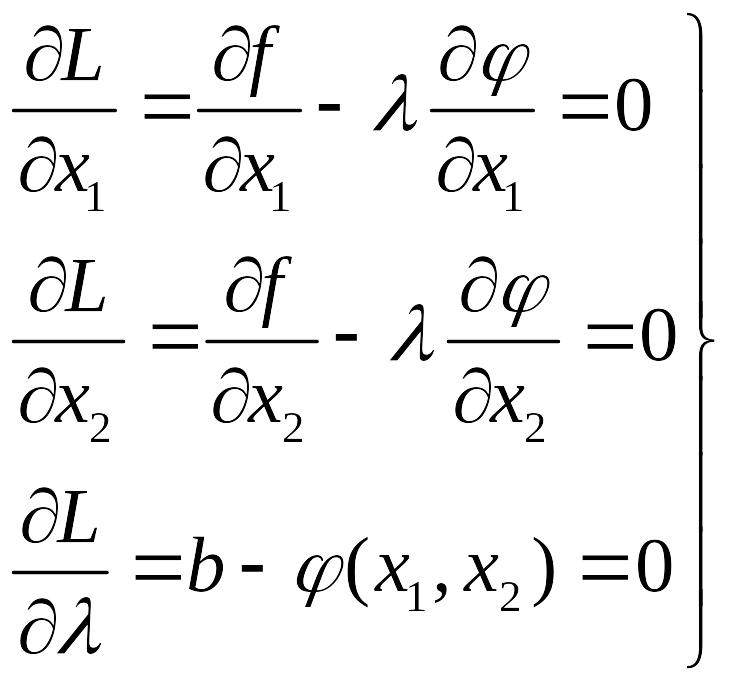(2)

с тремя неизвестными x_1, x_2, , из которой можно определить эти неизвестные. Есть и достаточные условия, при выполнении которых решение (x_1, x_2, ) системы (2) определяет стационарную точку, в которой f достигает экстремума. Этот вопрос решается на основе изучения знака второго дифференциала d²L функции (1). Поскольку в стационарной точке полный дифференциал функции равен 0, т.е.

и кроме того, , то второй дифференциал функции (1)

Функция f имеет в стационарной точке (x_1, x_2, ) условный максимум, если в ней d²L<0, и условный минимум, если d²L>0.

Аналогично находится условный экстремум функции трех и большего числа переменных при наличии одного или нескольких дополнительных ограничений (число которых должно быть меньше числа переменных). В этом случае приходится вводить в функцию Лагранжа столько неопределенных множителей, сколько имеется дополнительных уравнений связи.

Последовательность решения классической задачи оптимизации методом множителей Лагранжа.

1. Составляется функция Лагранжа

2. Находятся все стационарные точки функции Лагранжа из системы уравнений

3. Из стационарных точек функции L, взятых без координат ₁, ₂ и т.д., выбираются такие, в которых функция f имеет условные экстремумы при наличии ограничений. Этот выбор осуществляется с помощью достаточных условий.

Экономический смысл множителей Лагранжа.

Если f интерпретировать как доход или стоимость, b_i – как затраты некоторых ресурсов, множители _i ,будут показывать, как изменится максимальный доход (или минимальная стоимость), если количество i-го вида ресурсов увеличится на единицу.