- •Определенный интеграл
- •Утверждены методической комиссией
- •31 Мая 2007 года
- •1. Несобственные интегралы
- •Несобственный интеграл первого рода (интеграл с бесконечным промежутком интегрирования)
- •Несобственный интеграл второго рода
- •2. Геометрические приложения определенного интеграла
- •Площадь плоской фигуры
- •П усть дан график функции в прямоугольной системе координат (рис. 1).
- •В итоге получаем .
- •2.2. Вычисление длины дуги плоской кривой
- •Пример. Вычислить длину дуги отрезка цепной линии.
- •Эту формулу можно упростить, подставив в формулу (1) вместо ординату точки в. Получим . Из известной формулы имеем
- •Тогда длина кривой определяется по формуле
- •2.3. Вычисление объемов
- •2.4. Вычисление площади поверхности вращения
- •3. Механические приложения определенного интеграла
- •Работа переменной силы
- •3.2. Давление жидкости на пластину
- •3.3. Центр масс, статический момент, момент инерции
- •Индивидуальные задания
- •Литература
- •1. Холина л. И. Определенный интеграл / л. И. Холина, ю. М. Вахромеев. – Новосибирск ниси, 1981, 24с.
Индивидуальные задания
Указания:
1) В задачах на вычисление работы удельный вес воды считать равным 10 кН/м3
2) В
задачах на вычисление моментов инерции
получить
формулы при условии, что задана плотность
вещества
![]() ,
из которого
сделано тело, и при условии, что задана
масса тела
.
,
из которого
сделано тело, и при условии, что задана
масса тела
.
Вариант 1
1. Вычислить определенные интегралы:
![]() ;
;
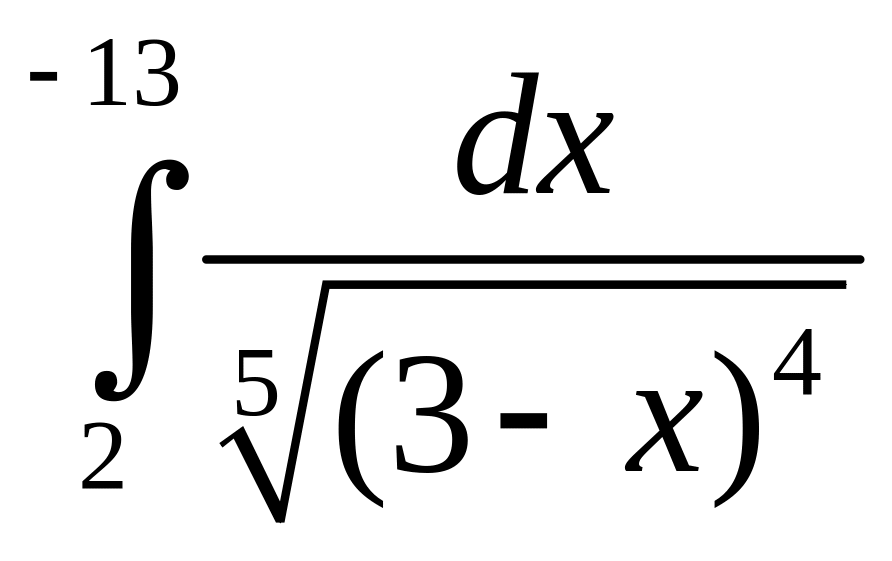 ;
;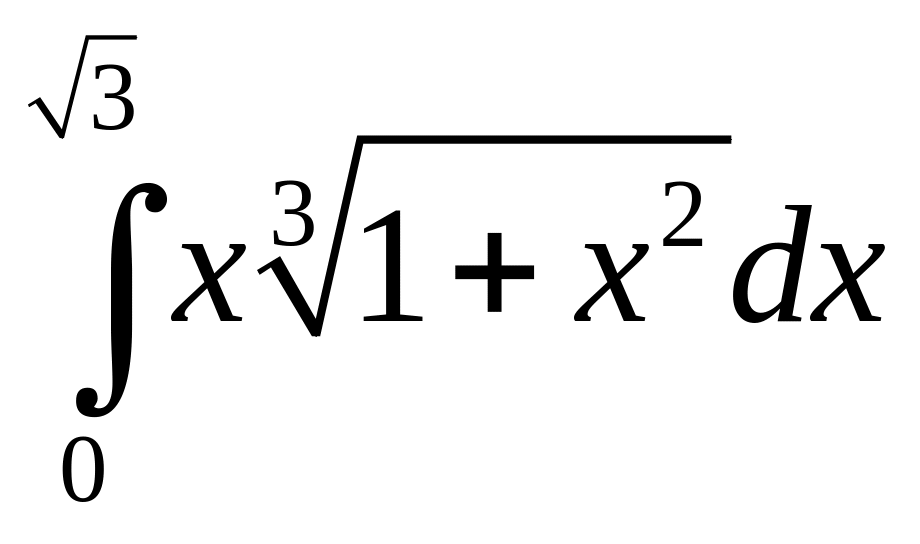 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из резервуара в виде правильной четырехугольной пирамиды со стороной основания 2 м и высотой 5 м.
8. Найти координаты центра масс однородной полуокружности , расположенной над осью .
9.
Найти момент инерции отрезка
![]() относительно оси, лежащей с ним в одной
плоскости, зная, что конец отрезка А
отстоит от оси на а
единиц,
конец В
– на b
единиц.
относительно оси, лежащей с ним в одной
плоскости, зная, что конец отрезка А
отстоит от оси на а
единиц,
конец В
– на b
единиц.
Вариант 2
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
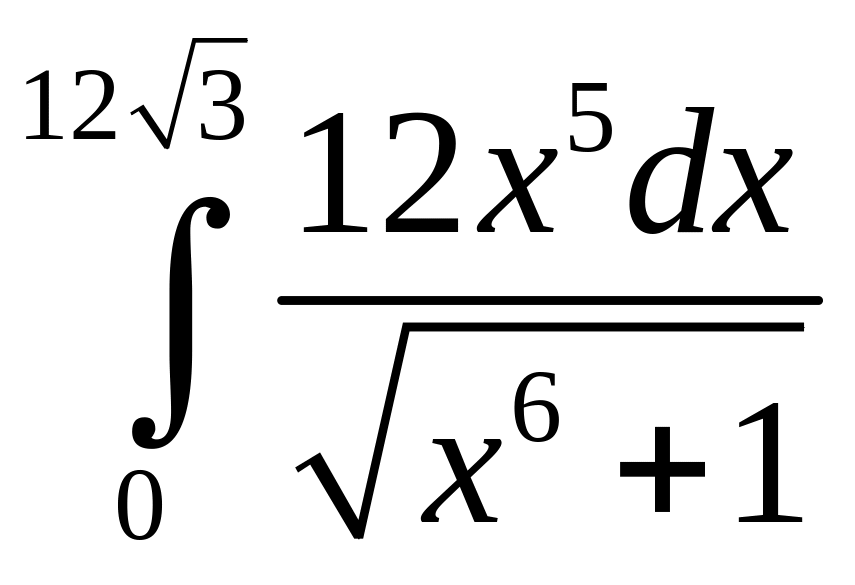 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из резервуара в виде правильной четырехугольной пирамиды со стороной основания 2 м и высотой 6 м, обращенной вершиной вниз.
8. Найти координаты центра масс первой арки циклоиды
![]() .
.
9. Найти момент инерции полуокружности радиуса R относительно ее диаметра.
Вариант 3
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из котла, имеющего форму сферического сегмента, высота которого 1,5 м и радиус 1 м.
8. Найти
координаты центра масс дуги астроиды
![]() ,
расположенной в третьем квадранте.
,
расположенной в третьем квадранте.
9. Найти момент инерции дуги линии
![]() относительно
оси
.
относительно
оси
.
Вариант 4
1. Вычислить определенные интегралы:
![]()
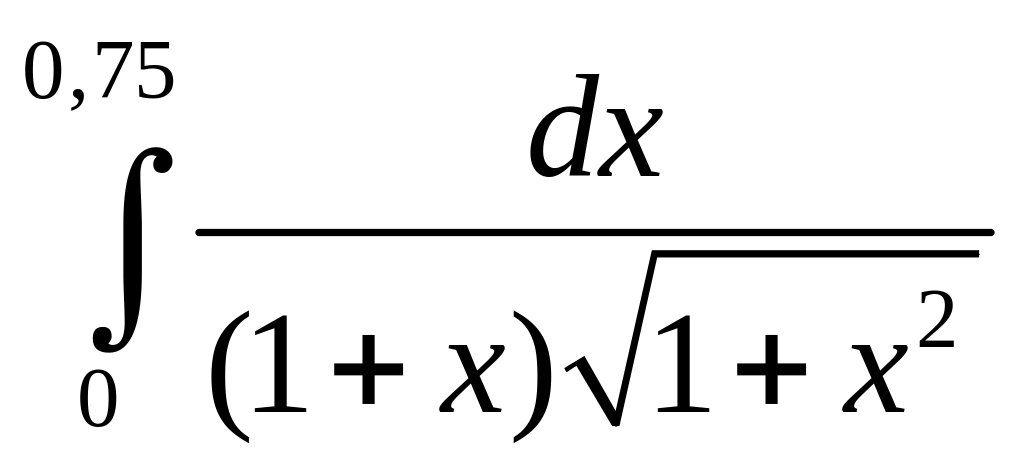 ;
;
 ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() отсеченная
прямой
отсеченная
прямой
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из полуцилиндра (корыта), радиус основания которого 1 м, длина 5 м.
8. Найти
координаты центра масс
дуги
окружности радиуса
,
стягивающей центральный угол
![]() .
.
9. Найти
момент инерции относительно обеих осей
координат одной арки циклоиды
![]() .
.
Вариант 5
1. Вычислить определенные интегралы:
![]() ;
; ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из усеченного конуса, у которого радиус верхнего основания 1 м, нижнего 2 м, высота 3 м.
8. Найти координаты
центра масс дуги цепной линии
![]() .
.
9. Найти момент
инерции прямоугольника со сторонами
и![]() относительно стороны
.
относительно стороны
.
Вариант 6
1. Вычислить определенные интегралы:
![]() ;
;
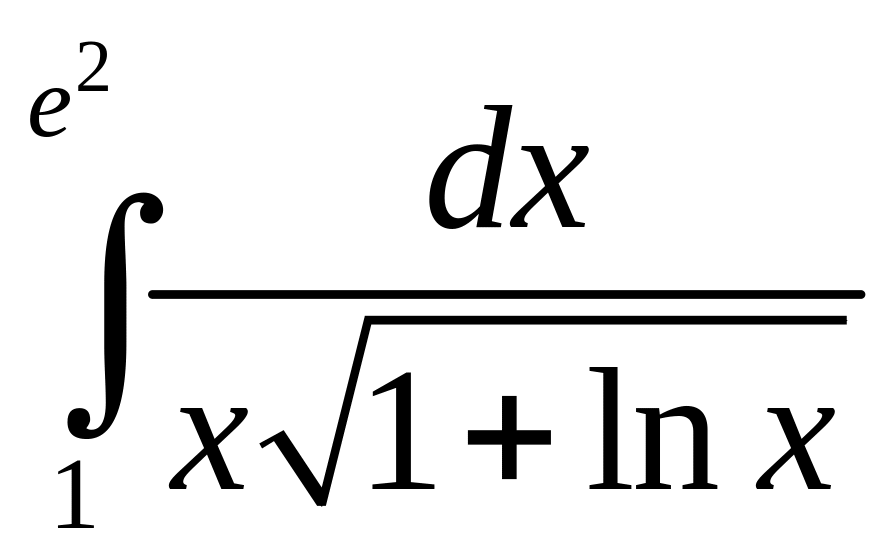 ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() отсеченная
прямой
отсеченная
прямой
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из желоба, перпендикулярное сечение которого является параболой. Длина желоба 5 м, ширина 4 м, глубина 4 м.
8. Найти координаты
центра масс дуги кардиоиды
![]() .
.
9. Найти момент инерции треугольника с основанием и высотой относительно основания.
Вариант 7
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии;
![]() ,
отсеченной прямой
,
отсеченной прямой
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из цилиндрической цистерны с радиусом основания 1 м, длиной 5 м.
8. Найти координаты
центра масс дуги логарифмической спирали
![]() .
.
9. Найти момент инерции четверти кольца, внешний радиус которого R, внутренний радиус относительно его центра.
Вариант 8
1. Вычислить определенные интегралы:
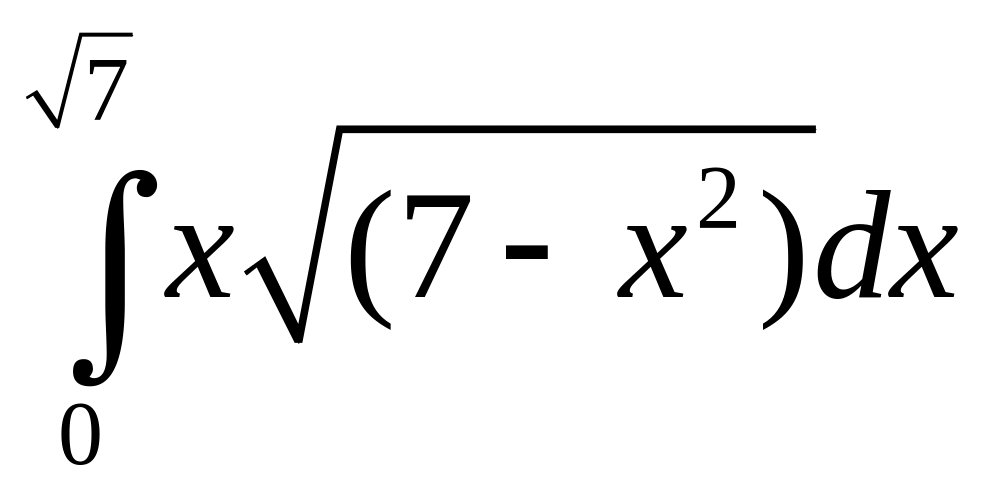 ;
;
![]() ;
;![]() .
.
2. Вычислить несобственные интегралы:
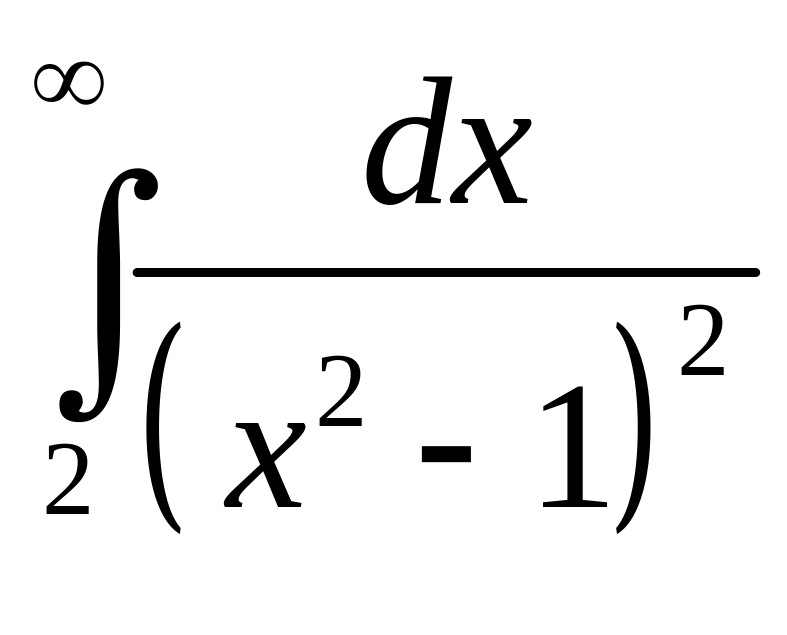 ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной треугольной пирамиды со стороной основания 2 м и высотой 5 м.
8. Найти координаты
центра масс
одной
арки циклоиды
![]() .
.
9. Найти момент инерции треугольника с основанием и высотой относительно прямой, параллельной основанию, проходящей через вершину.
Вариант 9
1. Вычислить определенные интегралы:
![]() ;
;
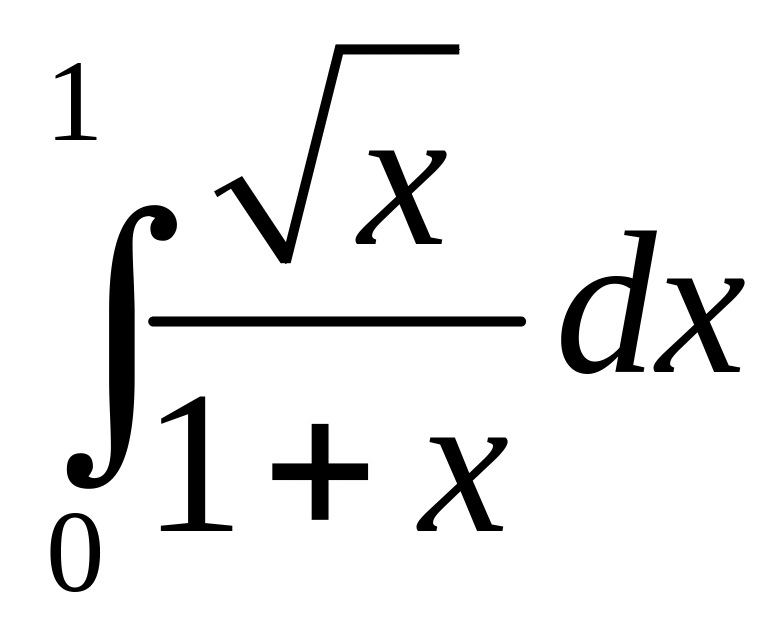 ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной треугольной пирамиды, обращенной вершиной вниз. Сторона основания 4 м, высота 6 м.
8. Найти
координаты центра масс дуги астроиды
![]() ,
расположенной в первом квадранте.
,
расположенной в первом квадранте.
9. Найти момент инерции треугольника с основанием a и высотой h относительно прямой, параллельной основанию, проходящей через центр тяжести.
Вариант 10
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из конуса, обращенного вершиной вниз. Радиус основания конуса 3 м, высота 5 м.
8. Найти координаты
центра масс дуги кривой:
![]() .
.
9. Найти момент инерции кольца, внешний радиус которого , внутренний радиус относительно его центра.
Вариант 11
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() y
= 4x
– 8;
y
= 4x
– 8;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() от
точки
от
точки
![]() до точки
до точки
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить
площадь поверхности, образованной
вращением дуги кривой вокруг указанной
оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из усеченного конуса, у которого радиус верхнего основания 3 м, нижнего – 1 м, высота 3 м.
8. Найти координаты центра масс кардиоиды .
9. Найти момент инерции полукруга радиуса R относительно его диаметра.
Вариант 12
1. Вычислить определенные интегралы:
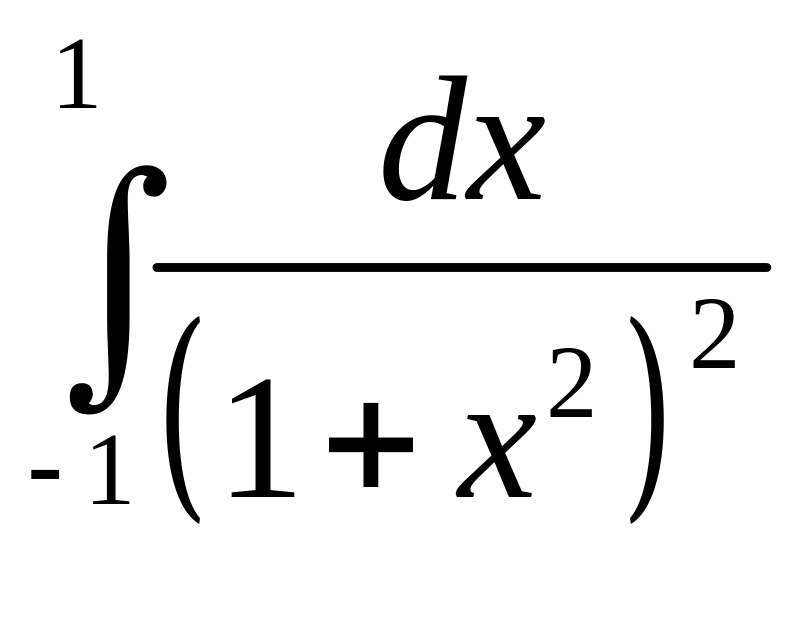 ;
;
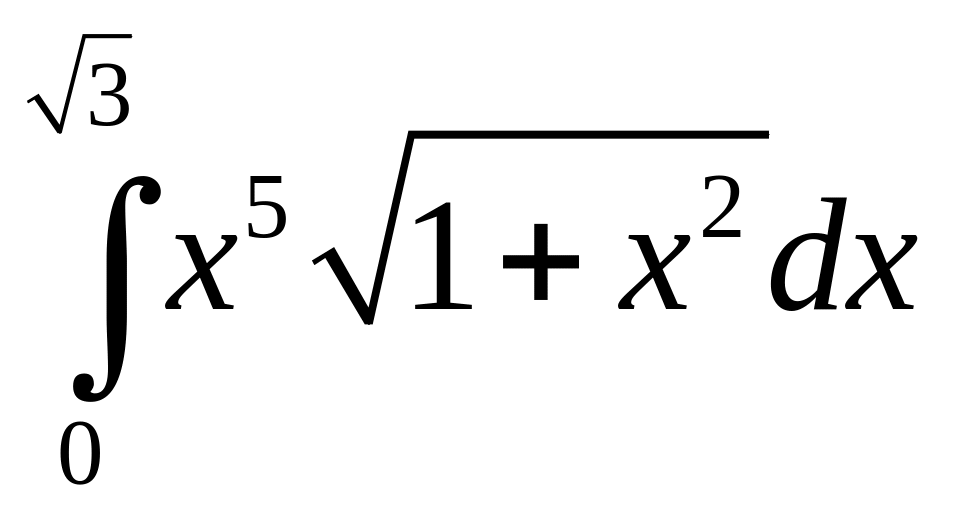 ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() 2)
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
отсеченная прямой
,
отсеченная прямой
![]() .
.
7. Высота правильной четырехугольной пирамиды Хеопса 140 м, ребро основания 200 м, удельный вес камня, из которого она сделана, равен 250 Н/м3. Вычислить работу, затраченную при ее постройке на преодоление силы тяжести.
8. Найти координаты
центра масс кривой
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
9. Найти момент инерции круга радиуса R относительно его центра.
Вариант 13
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
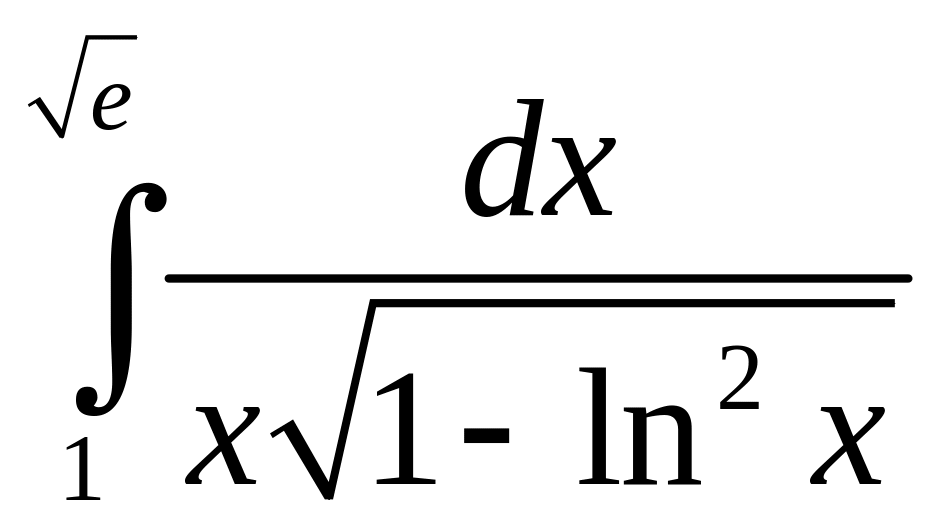 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
.
;
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Какую работу нужно произвести, чтобы насыпать кучу песка в форме усеченного конуса высотой 5 м, имеющего радиусы оснований 4 м и 1 м. Удельный вес песка 20 Н/м3. (Песок поднимают с поверхности земли, на которой покоится большее основание).
8. Найти координаты центра масс дуги развертки окружности:
![]()
![]() .
.
9. Найти момент инерции эллипса с полуосями и относительно обеих его осей.
Вариант 14
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из параболоида вращения, радиус основания которого 2 м, высота 2 м.
8. Найти
координаты центра масс
кривой
![]() ,
заключенной между лучами
,
заключенной между лучами
![]() .
.
9. Найти момент инерции эллипса с полуосями и относительно его центра.
Вариант 15
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
.
;
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() полярная ось.
полярная ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из половины эллипсоида вращения, радиус основания которого 1 м, высота 1 м.
8. Найти координаты центра масс кривой:
![]() .
.
9. Найти момент инерции цилиндра, радиус основания которого , высота , относительно его оси.
Вариант 16
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
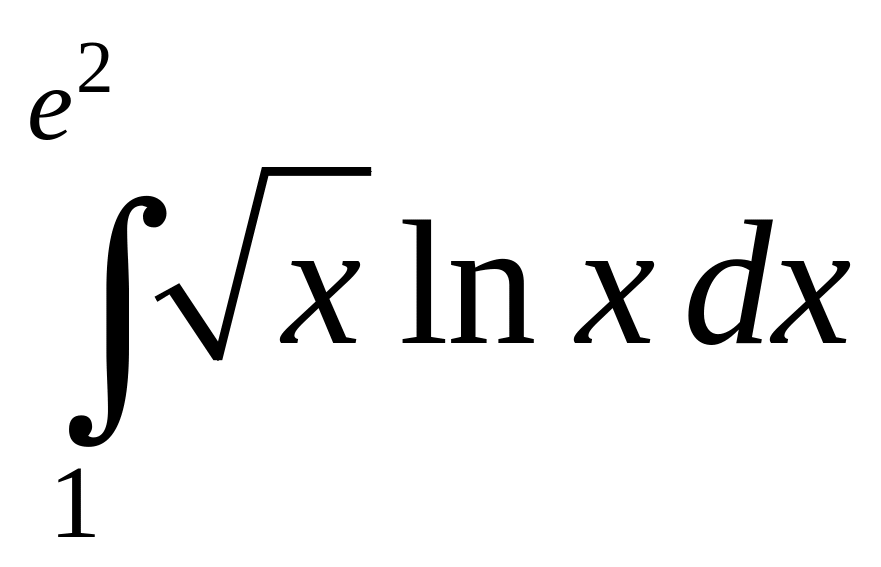 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2
вокруг асимпоты.![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() отсеченная
прямой
отсеченная
прямой
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной четырехугольной усеченной пирамиды со стороной верхнего основания 2 м, нижнего 4 м и высотой 1 м.
8. Найти координаты
центра масс треугольника, стороны
которого лежат
на прямых
![]() .
.
9. Найти момент инерции конуса, радиус основания которого , высота , относительно его оси.
Вариант 17
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() между точками
пересечения с осью
между точками
пересечения с осью
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1) полярная ось;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() отсеченная
прямой
отсеченная
прямой
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной шестиугольной пирамиды со стороной основания 1 м и высотой 2 м.
8. Найти
координаты центра масс плоской фигуры,
ограниченной эллипсом
![]() и осями
координат
и осями
координат
![]() .
.
9. Найти момент инерции шара радиуса относительно его диаметра.
Вариант 18
1. Вычислить определенные интегралы:
 ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
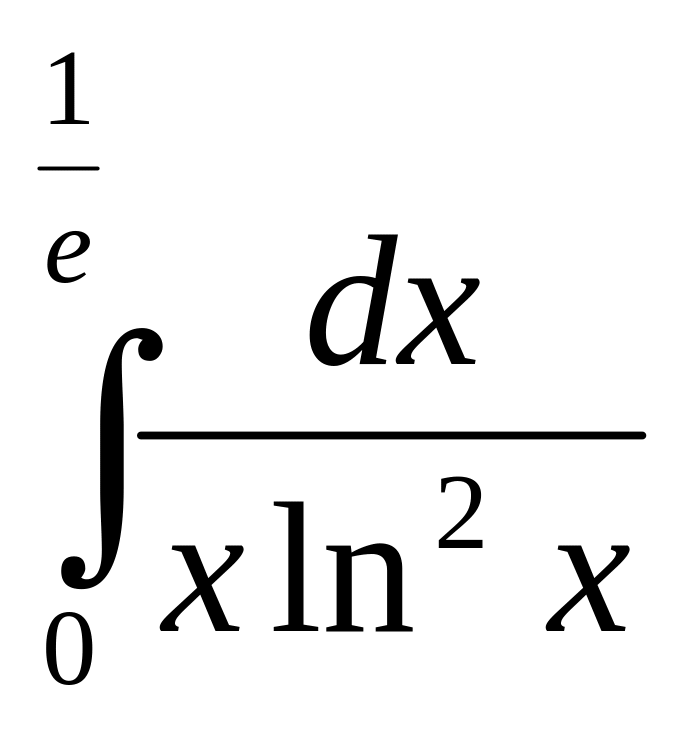 ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
.
;
4)
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной шестиугольной пирамиды, обращенной вершиной вниз. Сторона основания 2 м и высота 6 м.
8. Найти координаты центра масс плоской фигуры, ограниченной первой аркой циклоиды
![]() и осью
.
и осью
.
9. Эллипс вращается вокруг одной из своих осей. Найти момент инерции эллипсоида вращения относительно оси вращения.
Вариант 19
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
;
2)
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из цилиндра, радиус основания которого 1 м, высота 3 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченой кривыми
![]() .
.
9. Найти момент инерции относительно оси вращения параболоида вращения, радиус основания которого , высота .
Вариант 20
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
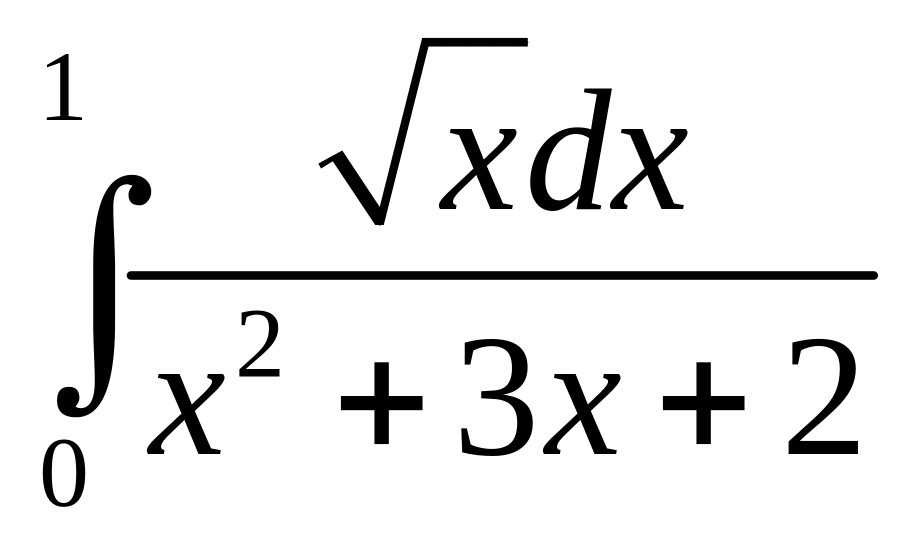 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
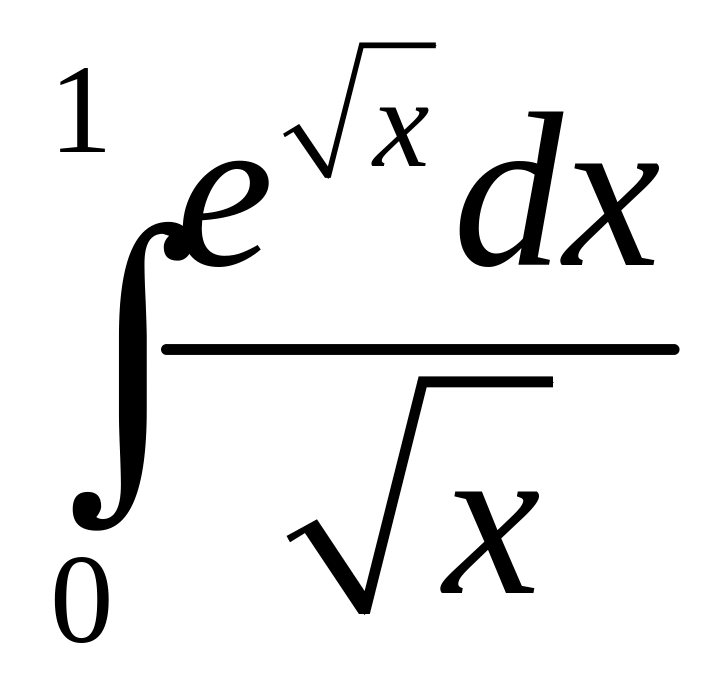 ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной шестиугольной усеченной пирамиды со стороной верхнего основания 1 м, нижнего 2 м и высотой 2 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной дугой
синусоиды
![]() и отрезком
оси
и отрезком
оси
![]() .
.
9.
Найти момент инерции относительно оси
тела, ограниченного однополостным
гиперболоидом
![]() и плоскостями
и плоскостями
![]() .
.
Вариант 21
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ,
(развертка
круга),
,
(развертка
круга),
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из желоба, перпендикулярное сечение которого является полуокружностью радиуса 1 м. Длина желоба 10 м.
8. Найти координаты центра масс плоской фигуры,
ограниченной
полуокружностью
![]() и осью
.
и осью
.
9.
Криволинейная
трапеция, ограниченная линиями
![]() ,
вращается вокруг оси
.
,
вращается вокруг оси
.
Найти момент инерции получающегося тела относительно оси вращения криволинейной трапеции.
Вариант 22
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
, полярная ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной шестиугольной усеченной пирамиды со стороной верхнего основания 2 м, нижнего – 1 м и высотой 2 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной дугой
параболы
![]() ,
,
![]() ,
осью
и прямой
,
осью
и прямой
![]() .
.
9. Криволинейная
трапеция, ограниченная линиями
![]() ,
вращается вокруг оси
.
Найти момент инерции получающегося
тела относительно оси вращения.
,
вращается вокруг оси
.
Найти момент инерции получающегося
тела относительно оси вращения.
Вариант 23
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() .
.
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из полусферы радиуса 2 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной дугой
параболы
,
,
осью
и прямой
![]() .
.
9. Найти момент инерции боковой поверхности цилиндра (тонкой трубы) радиус основания которого , высота , относительно его оси.
Вариант 24
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
3)
;
3)
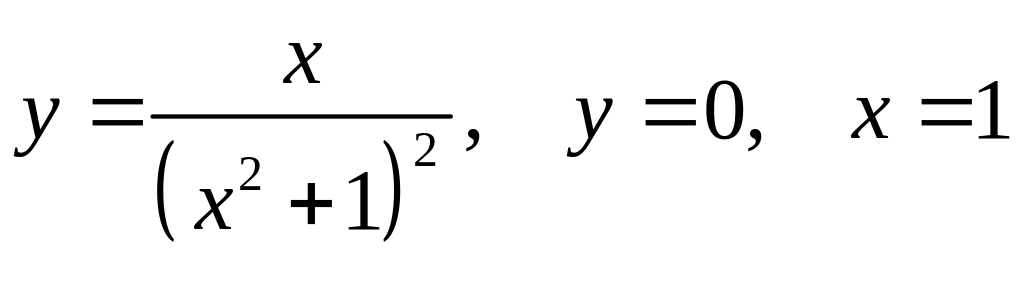 ;
;
4)
![]() (лист
Декарта), (перейти к полярным координатам).
(лист
Декарта), (перейти к полярным координатам).
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости, удельный вес которой γ = 24 кН/м3, из правильной четырехугольной усеченной пирамиды со стороной верхнего основания 2 м, нижнего 4 м и высотой 2 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной замкнутой линией
![]() .
.
9. Найти момент инерции боковой поверхности конуса (воронки) радиус основания которого , высота , относительно его оси.
Вариант 25
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости из правильной шестиугольной пирамиды со стороной основания 1 м, высотой 2 м, удельный вес жидкости γ = 24 кН/м3.
8.
Найти координаты центра масс плоской
однородной фигуры, ограниченной осями
координат и дугой
астроиды
![]() ,
расположенной в первом
квадранте.
,
расположенной в первом
квадранте.
9. Найти момент инерции поверхности шара (сферы) радиуса относительно его диаметра.
Вариант 26
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
 .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() (петля).
(петля).
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2) .
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости из правильной четырехугольной пирамиды со стороной основания 2 м и высотой 4 м, удельный вес жидкости γ = 24 кН/м3.
8. Найти координаты центра масс плоской однородной фигуры, ограниченной сектором круга радиуса с центральным углом, равным .
9. Найти момент инерции однородной дуги астроиды , расположенной в первой четверти.
Вариант 27
1. Вычислить определенные интегралы:
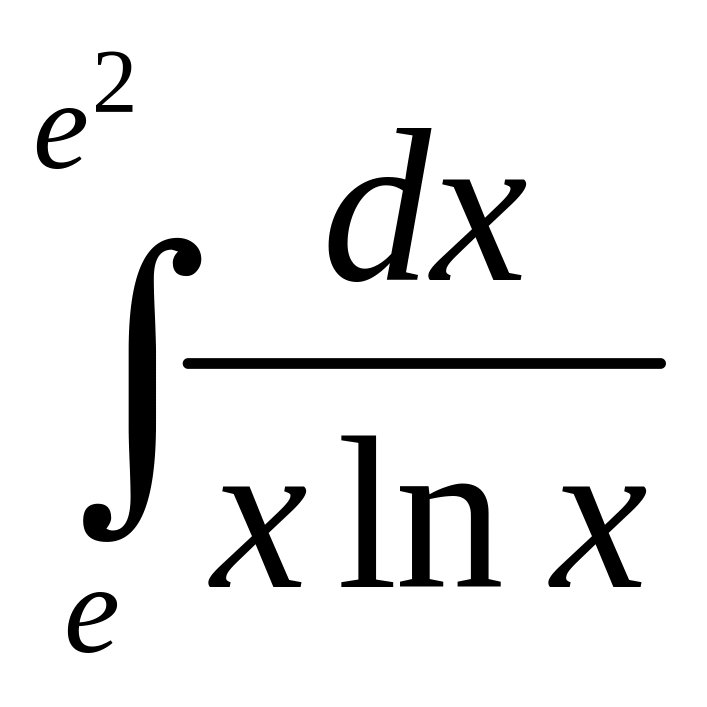 ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
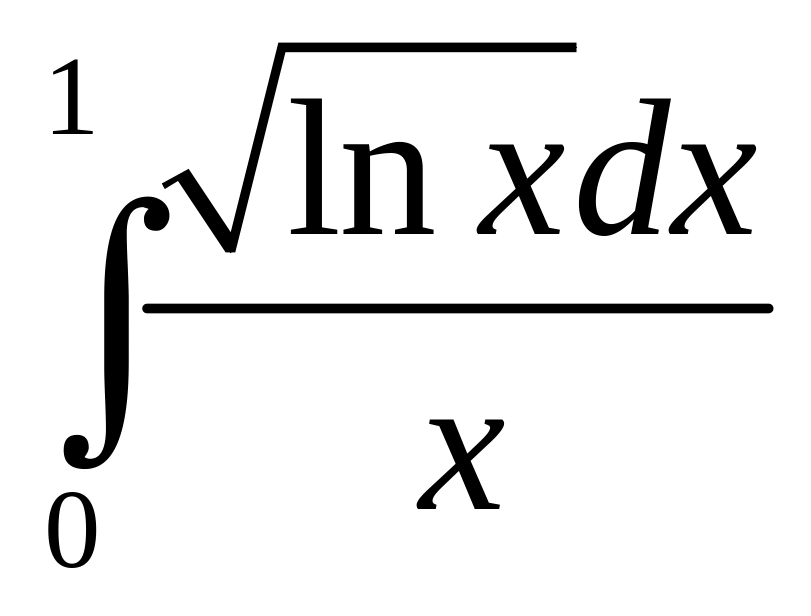 ;
;
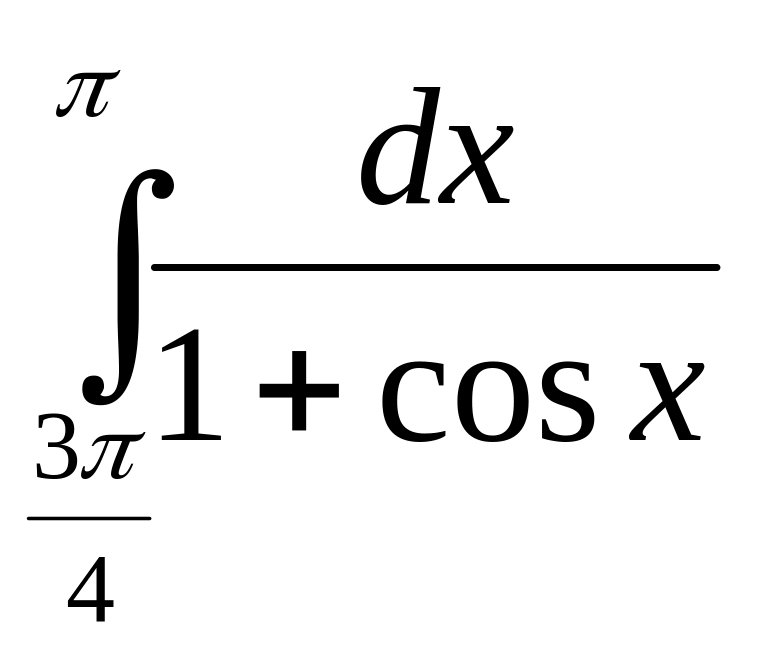 .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1) ;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() между прямыми
между прямыми
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание воды из правильной шестиугольной усеченной пирамиды со стороной верхнего основания 1 м, нижнего – 2 м и высотой 2 м.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной кардиоидой
![]() .
.
9. Найти момент инерции относительно оси окружности .
Вариант 28
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости из правильной треугольной пирамиды со стороной основания 3 м и высотой 6 м, удельный вес жидкости γ = 20 кН/м3.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной первой петлей лемнискаты
Бернулли
![]()
9. Найти момент инерции четверти окружности , расположенной в первом координатном углу, если в каждой ее точке линейная плотность пропорциональна произведению координат точки.
Вариант 29
1. Вычислить определенные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат
![]() .
.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости из конуса, радиус основания которого равен 2 м, высота 3 м, удельный вес жидкости γ = 20 кН/м3.
8. Найти координаты
центра масс плоской однородной фигуры,
ограниченной осями координат и кривой
![]() .
.
9. Найти момент инерции окружности относительно ее диаметра.
Вариант 30
1. Вычислить определенные интегралы:
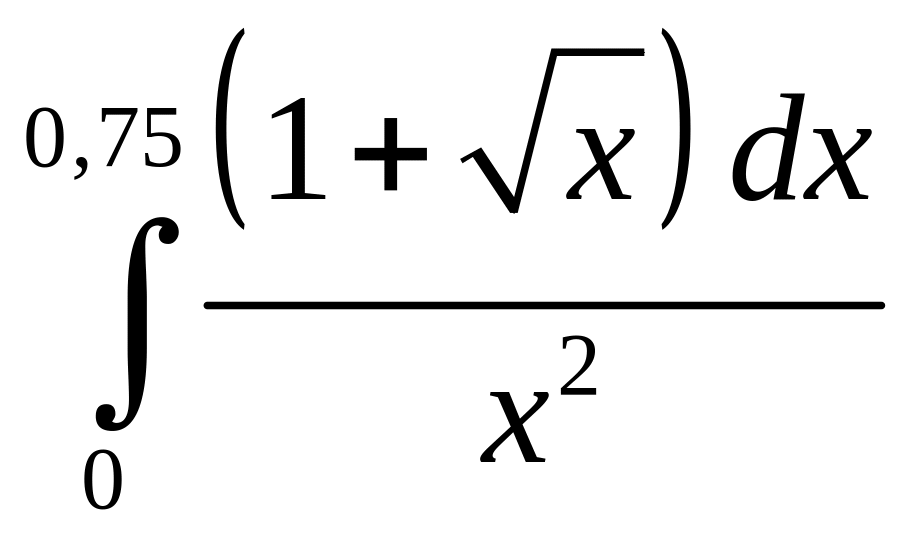 ;
;
![]() ;
;
![]() .
.
2. Вычислить несобственные интегралы:
![]() ;
;
![]() ;
;
![]() .
.
3. Вычислить площадь фигуры, ограниченной указанными линиями:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4. Вычислить длину дуги данной линии:
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
5. Вычислить объем тела, полученного вращением фигуры, ограниченной данными линиями, вокруг указанной оси:
1)
![]() ;
;
2)
![]() .
.
6. Вычислить площадь поверхности, образованной вращением дуги кривой вокруг указанной оси координат:
![]() ,
полярная
ось.
,
полярная
ось.
7. Вычислить работу, которую необходимо затратить на выкачивание жидкости из усеченного конуса, радиус верхнего основания которого равен 1 м, нижнего 2 м, высота 2 м, удельный вес жидкости γ = 21 кН/м3
8. Найти координаты центра масс плоской однородной фигуры, ограниченной полукубической параболой
![]() и прямой
и прямой
![]() .
.
9. Найти момент инерции четверти круга радиуса относительно его центра.
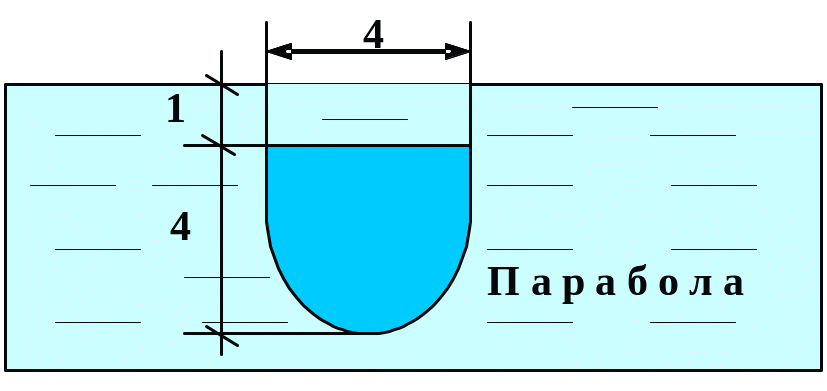
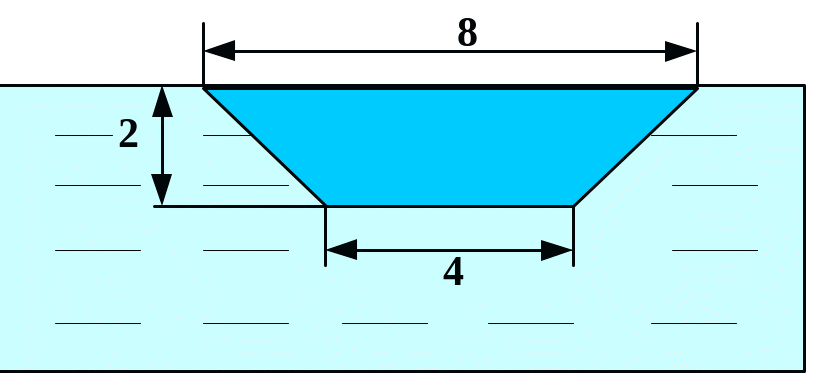
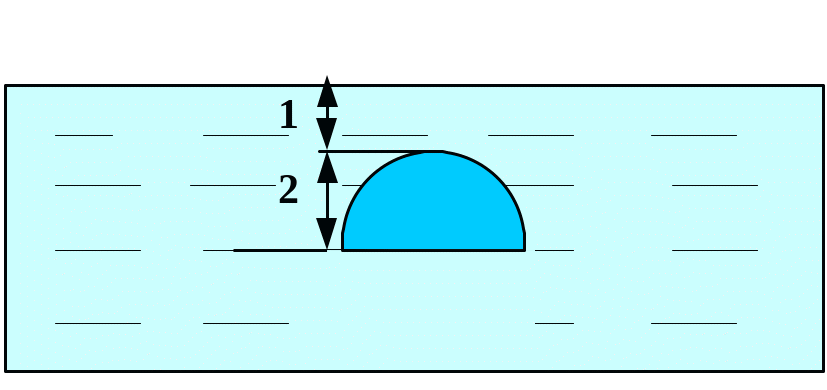
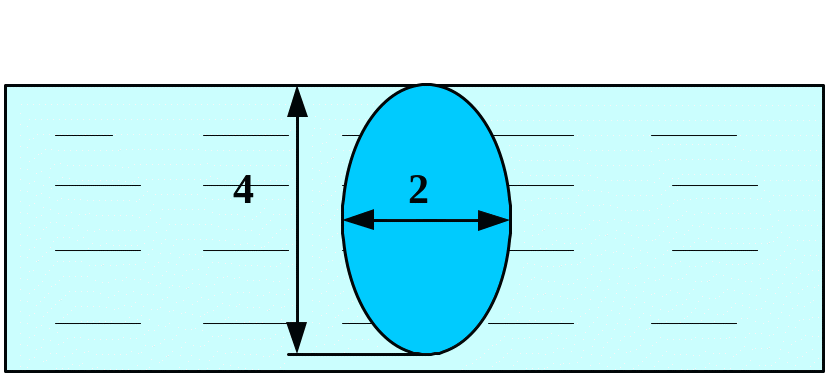
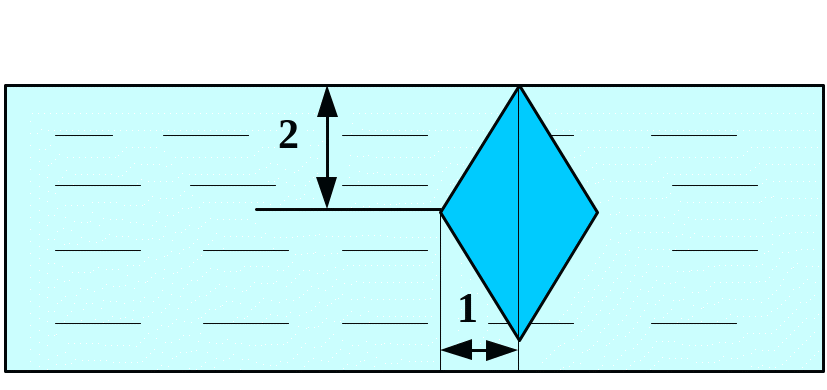
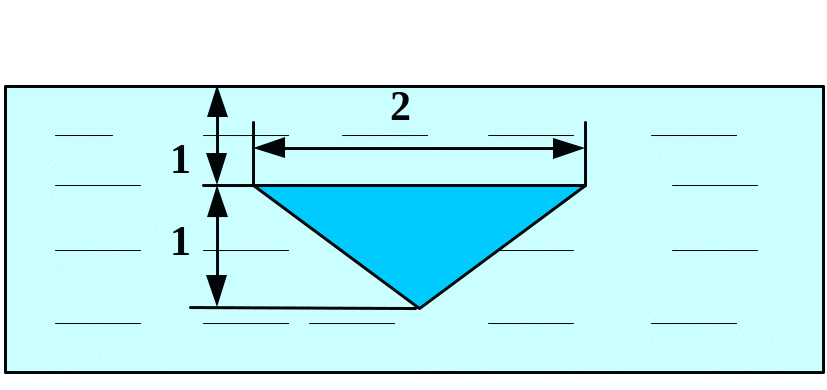
Вычислить силу давления воды на пластину, вертикально погруженную в воду, считая, что удельный вес воды равен10 кН/м3.
В
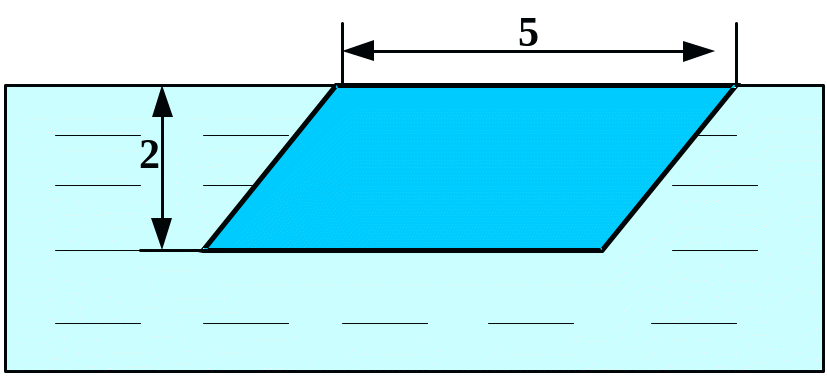
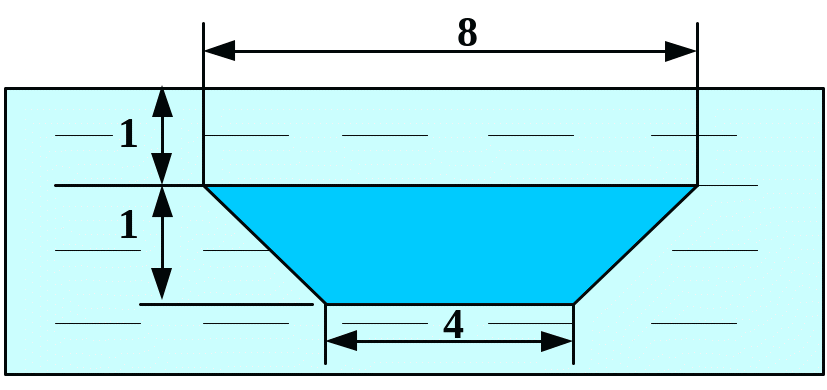
1
Вариант 3 Вариант 4
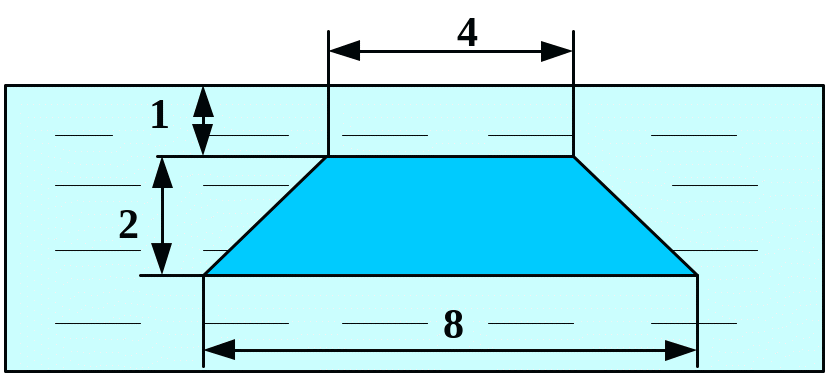
Вариант 5 Вариант 6

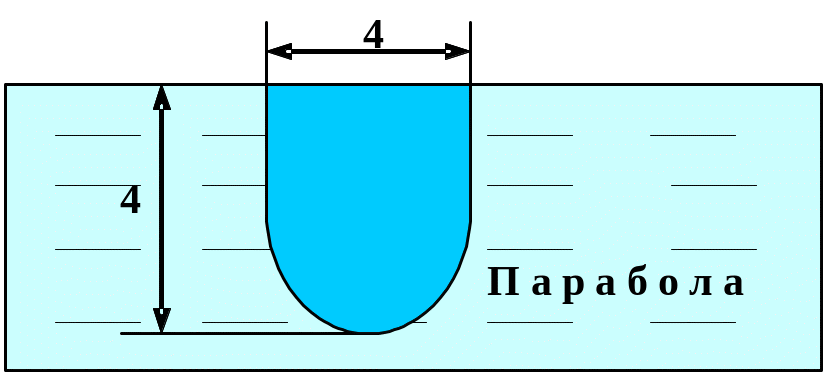
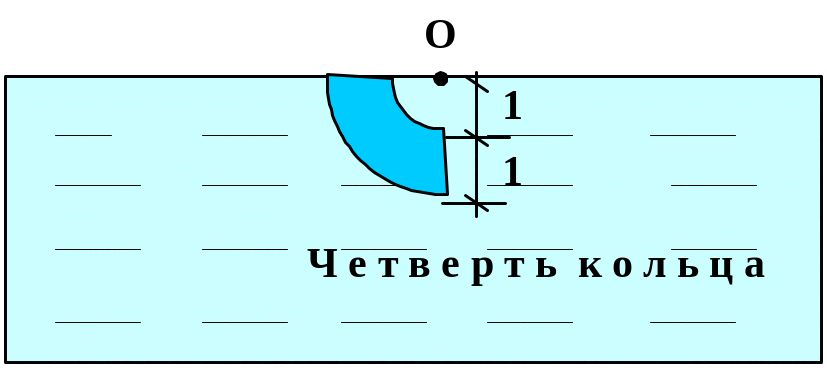
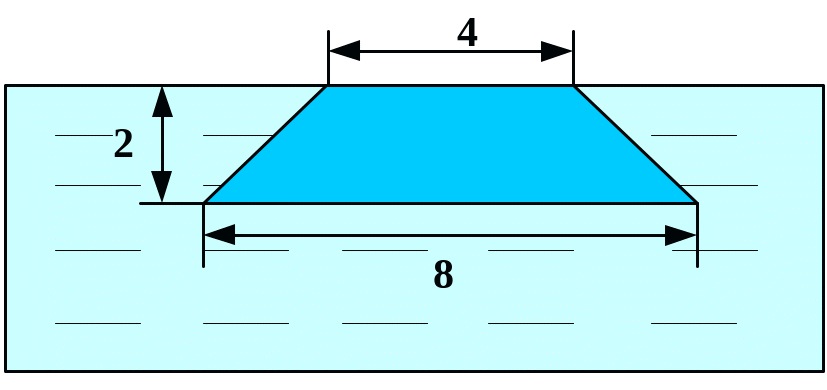
Вариант 9 Вариант 10
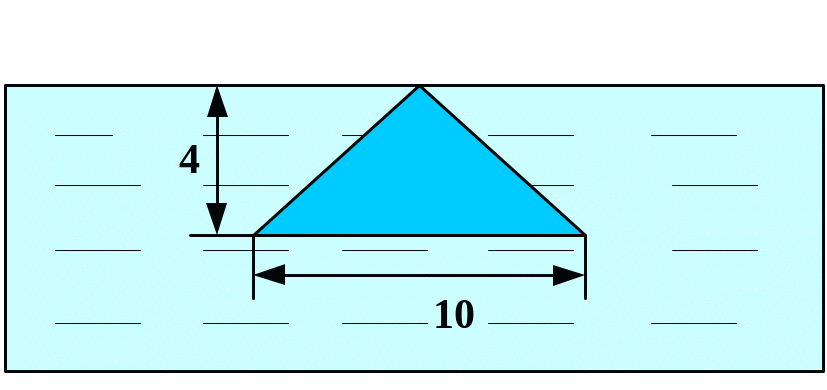
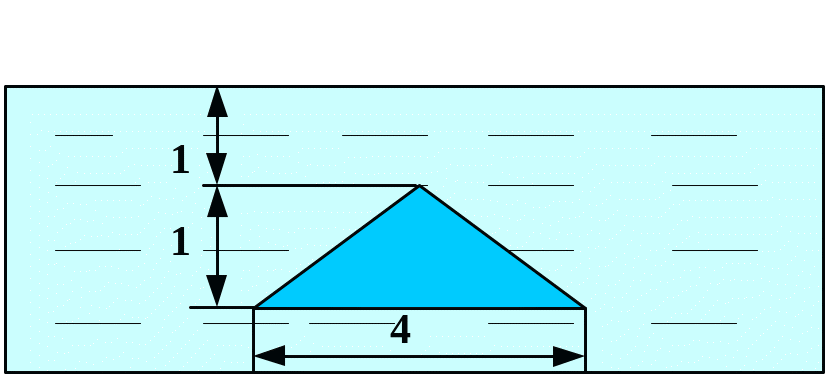
. 10 .
Вариант 11 Вариант 12
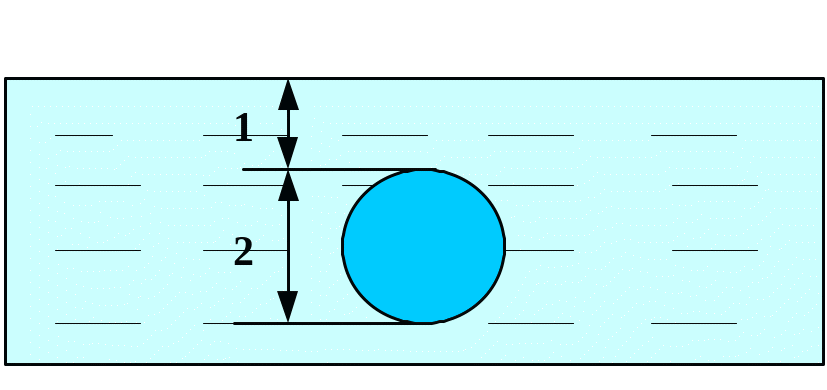
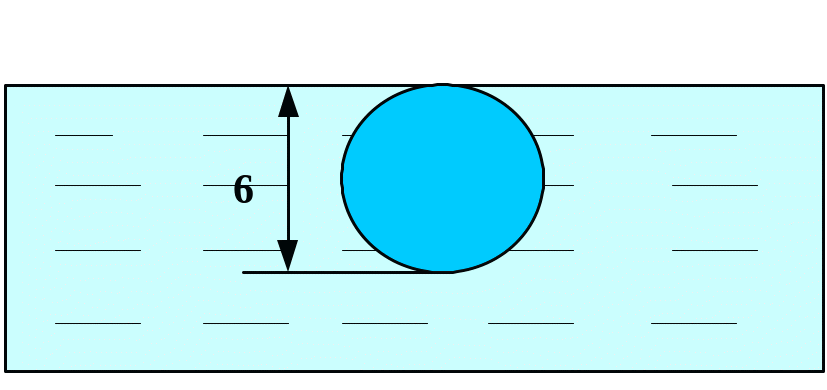
12
Вариант 13 Вариант 14
1
![]()
13 14

Вариант 17 Вариант 18
Вариант 19
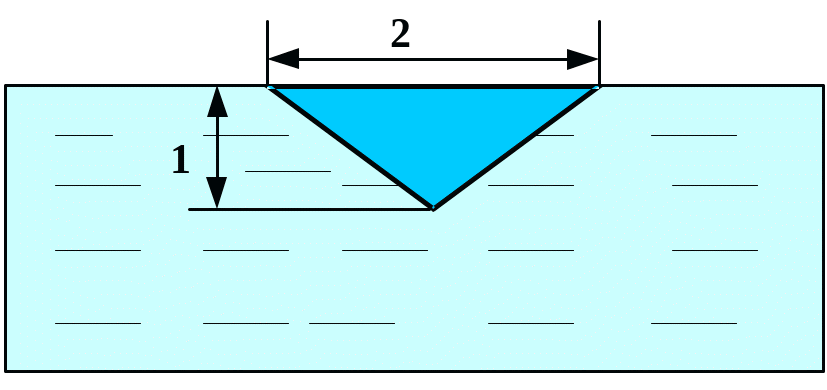
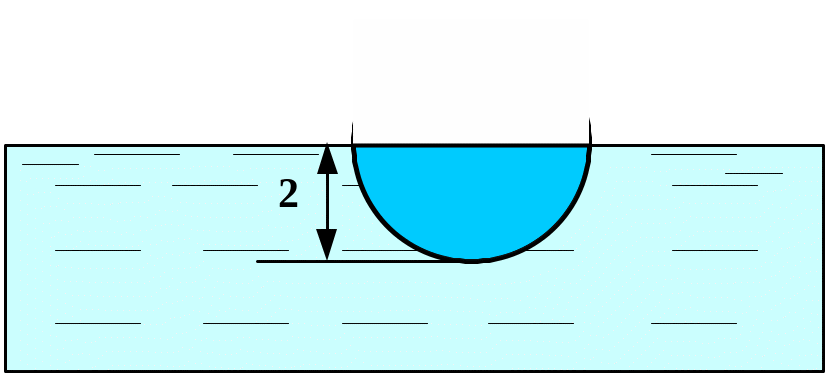
Вариант 21 Вариант 22
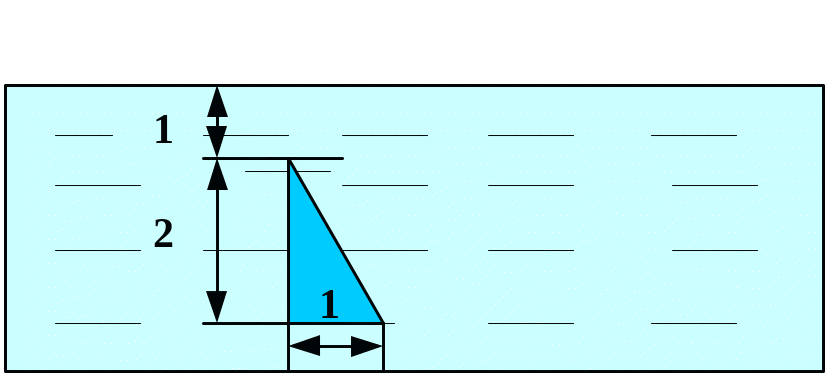
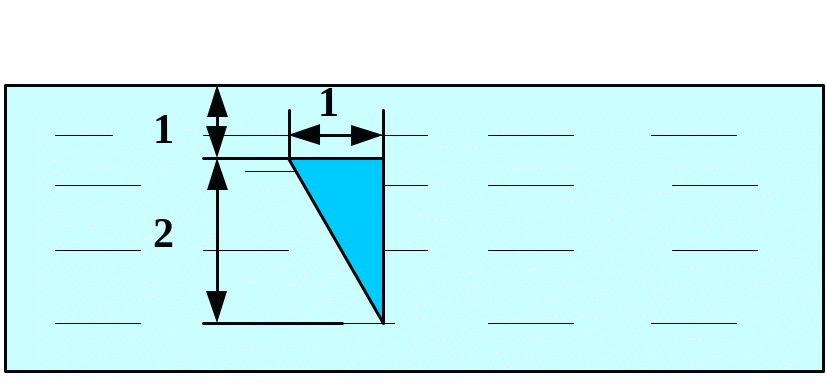
Вариант 23 Вариант 24
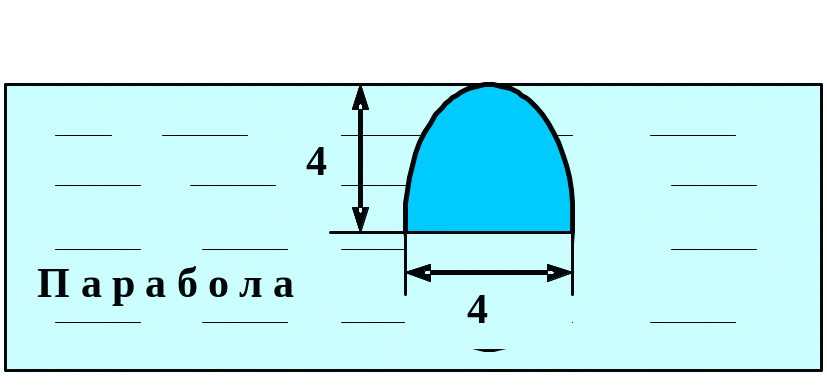
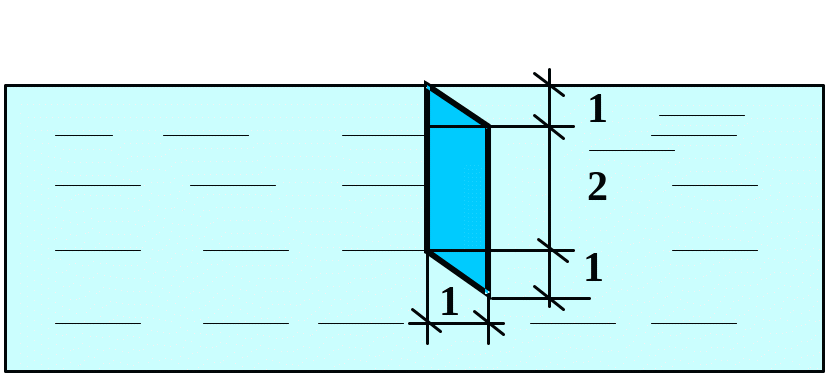
24
Вариант 25 Вариант 26


Вариант 27 Вариант 28
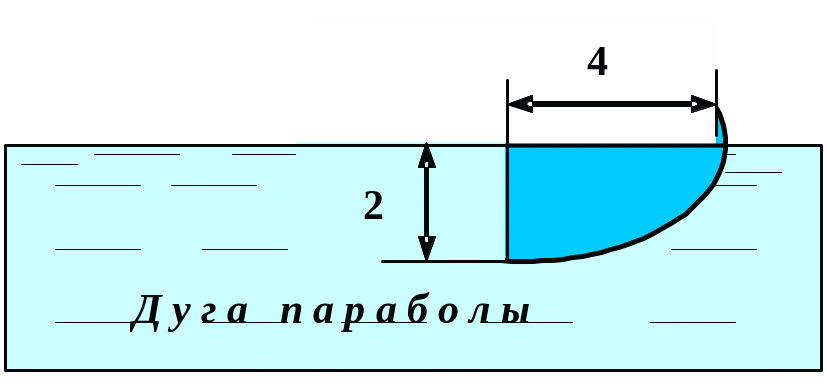
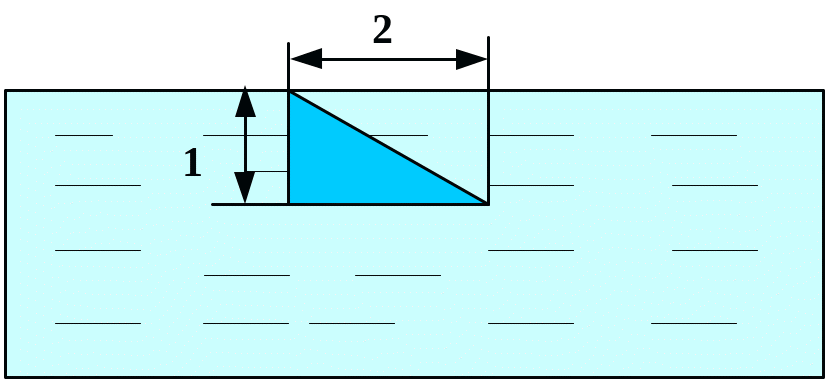
Вариант 29 Вариант 30