3.3. Центр масс, статический момент, момент инерции

Р

ассмотрим систему материальных точек . Пусть – масса i-й точки, – ее радиус-вектор относительно некоторой системы координат.

Центром масс системы материальных точек называется точка с пространства, определяемая радиус-вектором

, (5)

где М – масса всей системы,

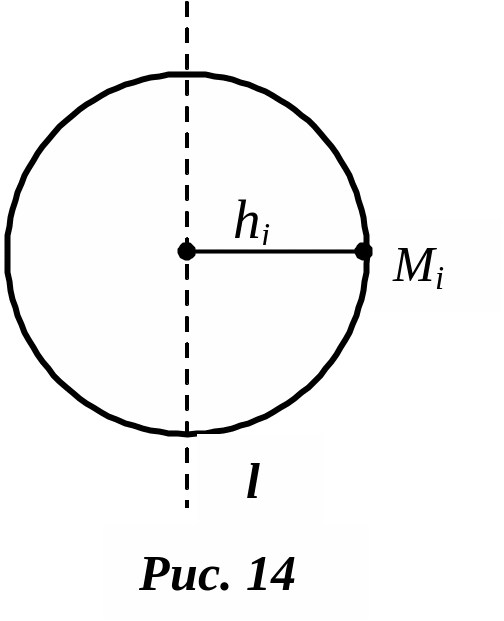
Пусть – расстояние точки массой до некоторой оси (рис. 14).

Тогда величина называется статическим моментом, а величина – моментом инерции системы относительно оси .

Статические моменты и моменты инерции характеризуют распределение масс в системе материальных точек.

Если массы не сосредоточены в отдельных точках, а распределены сплошным образом, заполняя линию, плоскую фигуру или объемное тело, то тогда для выражения центра масс, статических моментов и моментов инерции вместо сумм используются интегралы. Формально это можно определить следующим образом.

П усть требуется определить положение центра масс некоторого тела. Разобьем тело на произвольные малые объемы , для которых, например, координата центра масс определяется по формуле

где x_i – координата x некоторой точки, лежащей внутри объема .

Затем перейдем к пределу, устремляя все к нулю, т.е. стягивая эти объемы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространенные на весь объем тела:

. (6)

А

налогичные формулы получаются и для других координат центра масс объема, а также и для координат центров масс площадей и линий.

Поясним сказанное под­робнее на конкретных примерах.

Сначала рассмотрим спо­собы определения центра масс однородных тел методом интегрирования.

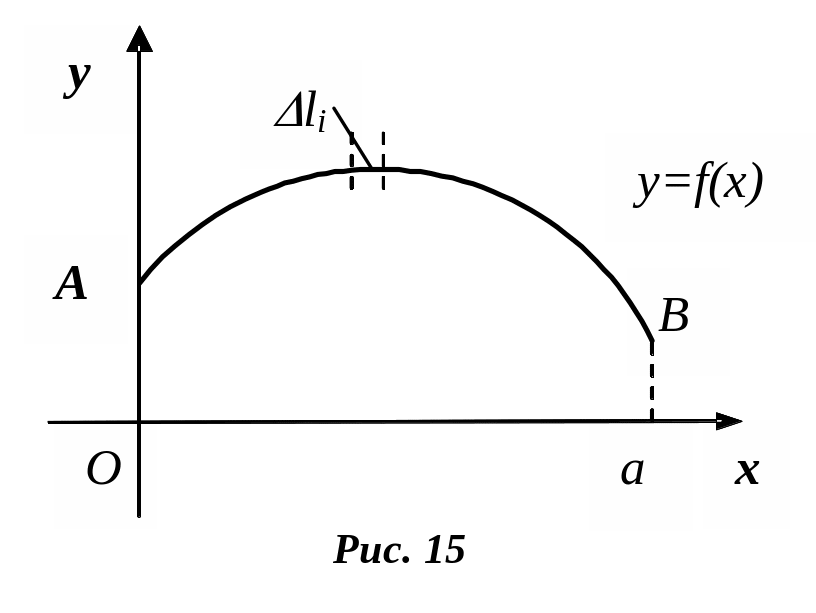
Центр масс плоской линии

Пусть дана материальная кривая АВ, уравнение которой имеет вид (рис. 15).

Предположим, что масса единицы длины (линейная плотность) линии является величиной постоянной. Выделим элемент линии . Пусть координаты выделенного элемента будут . Масса выделенного элемента будет . Используя формулу (5) и сокращая в числителе и знаменателе постоянный множитель , получим соотношение для центра масс всей линии АВ.

Суммирование ведется по всей длине кривой.

, .

Если функция непрерывна и имеет непрерывную производную, то стоящие в числителе и знаменателе каждой дроби суммы при имеют пределы, равные пределам соответствующих интегральных сумм. Таким образом, координаты центра масс линии АВ выражаются интегралами:

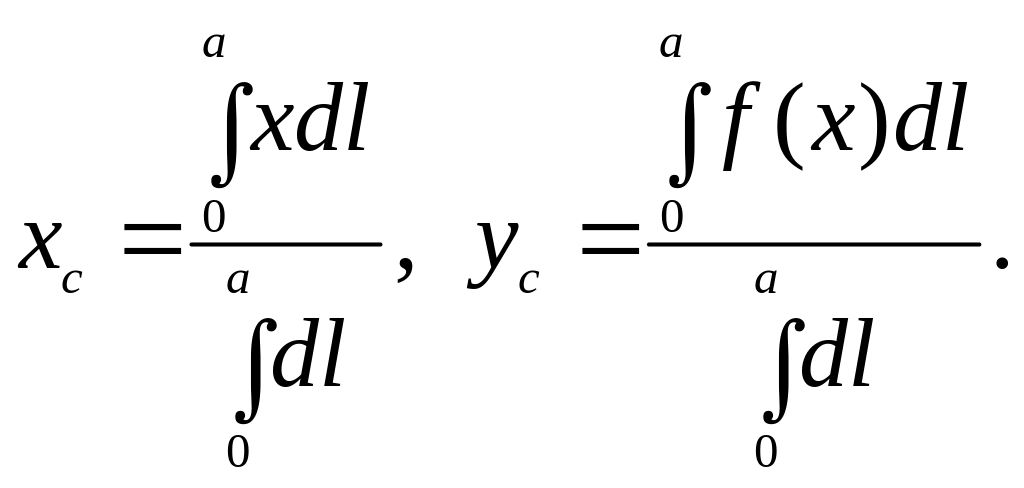
Длина дуги определяется соотношением

где – производная функции по .

Учитывая это, получим

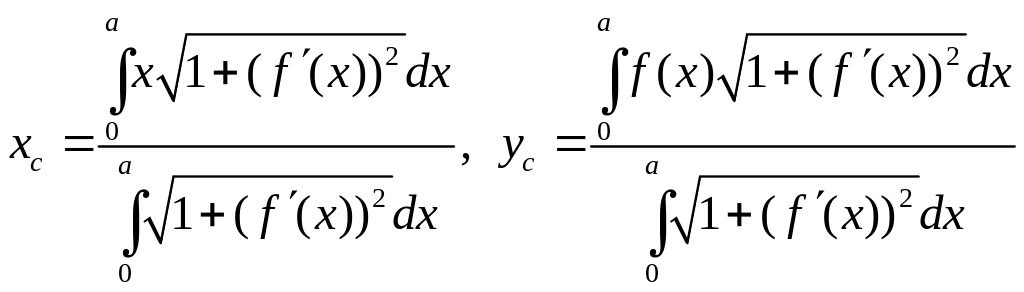. (7)

Остановимся на определении статического момента относительно оси рассмотренной ранее кривой . Выделим снова элемент кривой . Предположим, что , а длина всей кривой равна . Тогда масса выделенного элемента также будет . Приняв этот элемент приближенно за материальную точку, лежащую на расстоянии от оси, для его статического момента получим выражение . Суммируя эти элементарные статические моменты по всей длине , получим

. Аналогично .

Статические моменты кривой позволяют легко установить положение ее центра тяжести . Точка С обладает тем свойством, что если в ней сосредоточить всю массу кривой, то момент этой массы относительно любой оси совпадает с моментом кривой относительно этой оси. Если рассмотреть моменты кривой относительно осей координат, то найдем

,

откуда .

Умножив правую и левую части формулы на , получим

.

Правая часть этого равенства есть площадь поверхности , полученной от вращения кривой АВ, в левой части равенства – длина окружности, описанной центром тяжести кривой при вращении ее вокруг оси , а – длина кривой. Следовательно, .

Этот результат формулируется в виде теоремы Гульдина–Паппа.

Величина поверхности, полученной от вращения кривой около некоторой непересекающей ее оси, равна длине дуги этой кривой, умноженной на длину окружности, описанной центром тяжести С кривой.

Эта теорема позволяет установить координату центра тяжести кривой, если известны ее длина и площадь описанной ею поверхности вращения.

П ример 1. Найти координаты центра масс полуокружности (рис. 16). Линейную плотность считать величиной постоянной.

Решение. Расположим полуокружность симметрично оси . Тогда . Для определения координаты воспользуемся формулой (7), получив предварительно некоторые вспо­мо­гательные соотношения:

,

,

.

Следовательно,

.

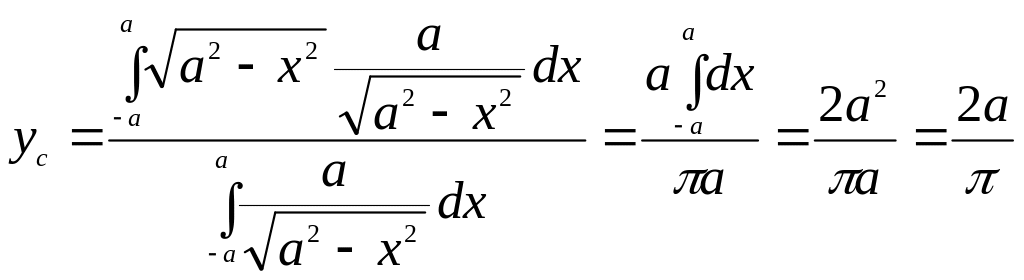Р

ешим эту же задачу, применяя теорему Гульдина–Паппа. Найдем координату . От вращения рассматриваемой полуокружности вокруг оси получается шар, площадь поверхности которого равна . По теореме Гульдина площадь той же поверхности равна , где – длина полуокружности. Следовательно, .

Ответ: .

Пример 2. Определить центр масс дуги окружности (рис. 17).

Решение. Рассмотрим дугу АВ радиуса с центральным углом . В силу симметрии центр масс этой дуги лежит на оси Ох. Найдем координату по формуле (6), заменив в ней элементы объема на элементы длины дуги:

,

где – длина всей дуги АВ, – выделенный элемент дуги. Координата выделенного элемента дуги будет . Подставляя эти значения в формулу и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим

.

Центр масс плоской фигуры

П

усть данная фигура, ограниченная линиями ,

, представляет собой плоскую фигуру, (рис. 18). Поверхностную плотность (т.е. массу единицы площади поверхности) будем считать постоянной и обозначим ее буквой . Выделим элемент поверхности (тонкую полоску) . Масса этого элемента будет равна произведению его площади на плотность. Предположим, что выделенный элемент представляет собой очень тонкий прямоугольник с основанием и высотой . Тогда получим, что его масса приближенно равна:

Приближенно центр масс этой полоски будет находиться в центре прямоугольника, т.е.

Суммируя теперь по всей площади в соответствии с формулой (5), получим:

, .

Переходя к пределу при , получим

,

П

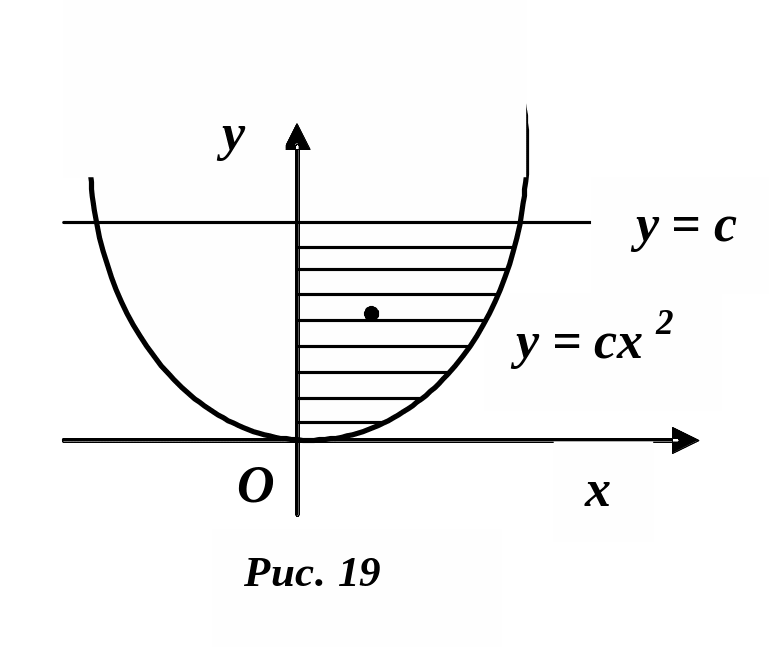
ример 1. Определить координаты центра масс сегмента параболы , отсекаемого прямой и прямой (рис. 19).

Решение. Определим функции для нашего случая . Переменная изменяется от нуля до 1. (При имеем ). Подставляем полученные значения в последние формулы, получаем

, .

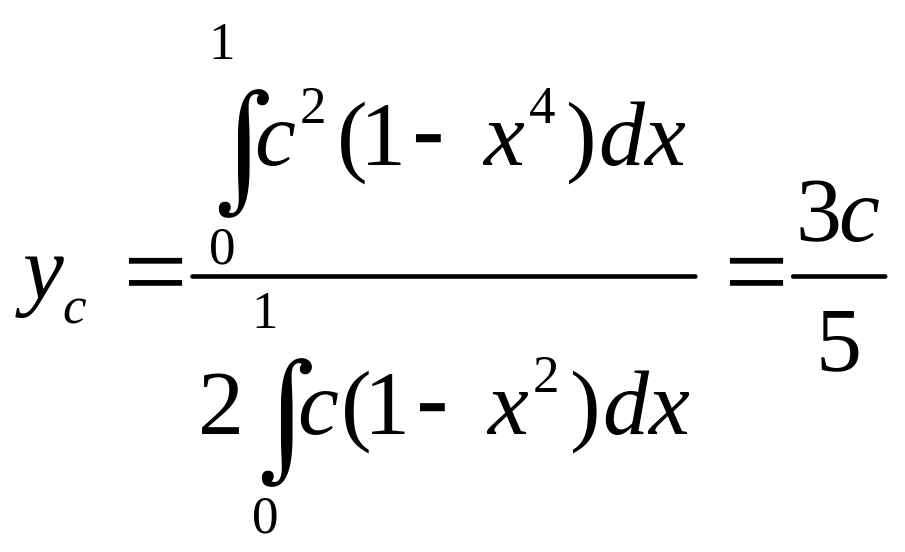О

твет: .

Пример 2. Определить координаты центра масс четверти фигуры, ограниченной эллипсом , полагая, что плотность во всех точках одинакова (рис.20).

Решение. Пусть . Воспользуемся формулой (5) применительно к координате . Так как плотность фигуры постоянная величина, то

,

где – площадь выделенного вертикального слоя ширины .

Так как , то

Перейдем к пределу в числителе и знаменателе. При этом заменим исходное уравнение эллипса его параметрическим уравнением . В результате этой замены . Следовательно,

.

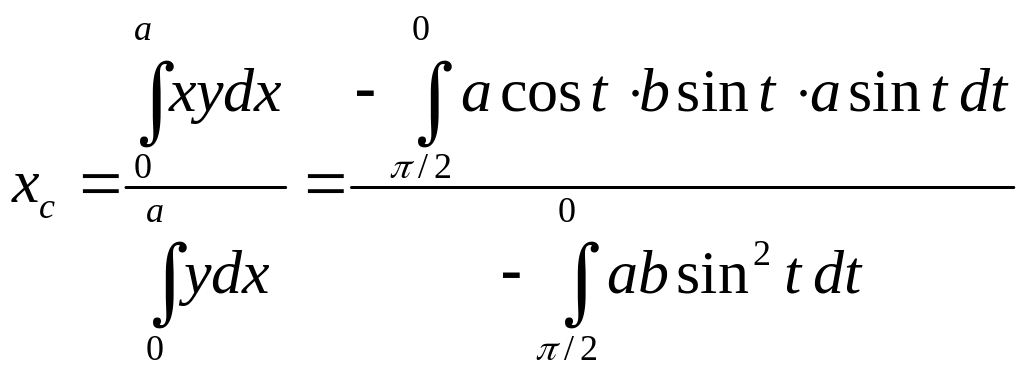Вычислим отдельно интегралы в числителе и знаменателе :

,

.

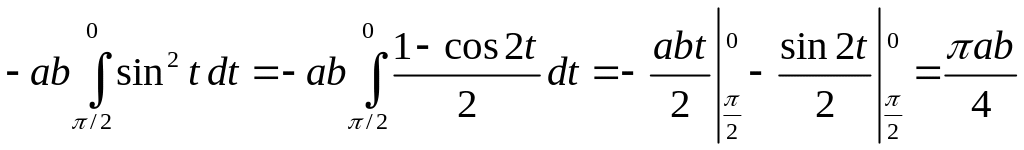Следовательно, . Аналогично находится .

Ответ: .

П

ример 3. Определить центр масс площади треугольника (рис. 21).

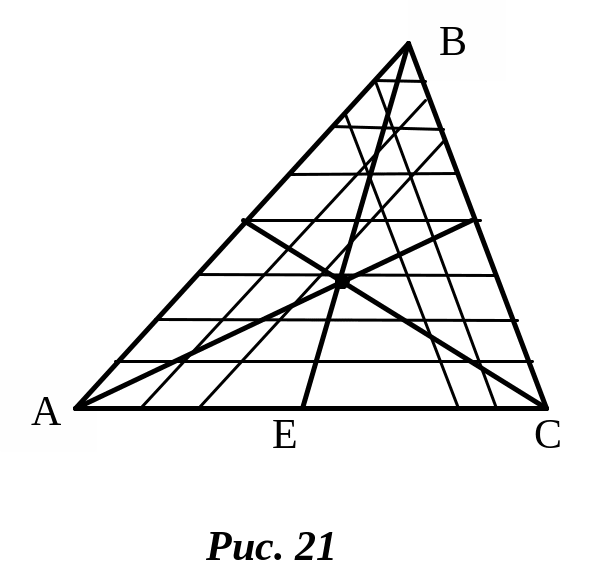
Решение. Разобьем площадь треугольника АВС прямыми, параллельными стороне АС, на узких полосок. Центры масс этих полосок будут лежать на медиане ВЕ треугольника. Следовательно, и центр масс всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан.

Ответ: Центр масс площади треугольника лежит в точке пересечения его медиан.

Пример 4. Определить центр масс площади кругового сектора (рис. 22).

Решение. Рассмотрим круговой сектор АОВ радиуса с центральным углом 2. Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на секторов. В пределе при неограниченном увеличении числа эти секторы можно рассматривать как плоские треугольники, центры масс которых лежат на дуге радиуса .

Следовательно, центр масс сектора АОВ совпадает с центром масс дуги , положение которого определяется по формуле

.

Ответ: .

В частности, для полукруга получим

Пример 5. Найти декартовы координаты центра масс:

а) кардиоиды , б) фигуры, ограниченной кардиоидой (рис. 8).

Решение: Так как кардиоида симметрична относительно оси , то координата центра масс . По той же причине для определения координаты можно рассмотреть только верхнюю часть кардиоиды. Пусть - статический момент кардиоиды относительно оси . Тогда

, ,

, , , , ,

,

.

.

.

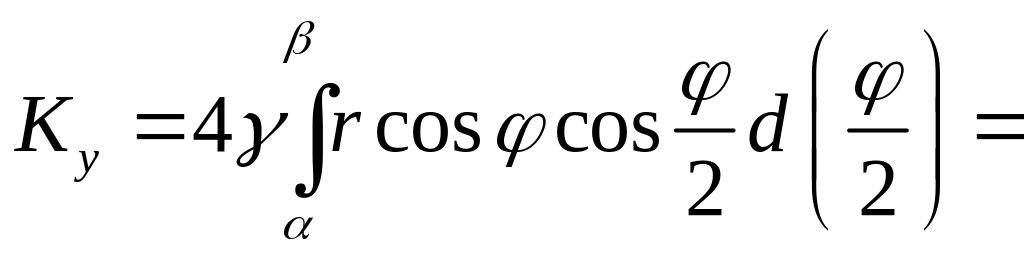
Вычислим отдельно эти два интеграла:

.

.

, .

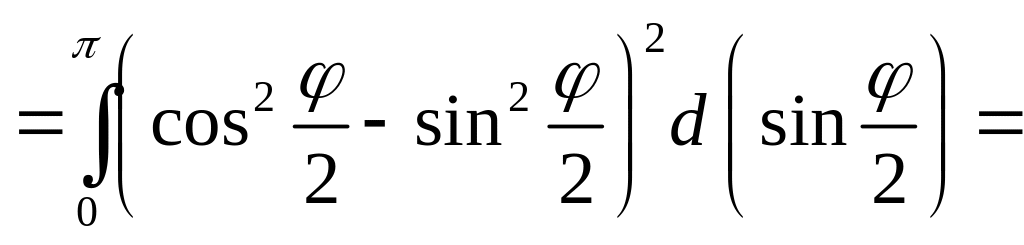
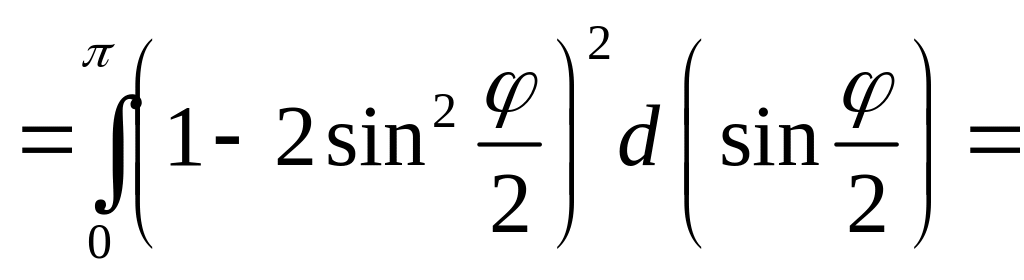
Ответ: .

Для кардиоиды, заданной уравнением будем иметь .

б) Для решения этой задачи можно так же, как и в случае а) воспользуемся формулой (5), переходя к параметрическому уравнению кардиоиды. Но проще поступить следующим образом. Так же, как и в случае определения центра масс кругового сектора разобьем мысленно площадь кардиоиды прямыми, проведенными из центра О полярной системы координат, на секторов. В пределе при неограниченном увеличении числа эти секторы можно рассматривать как плоские треугольники, центры масс которых лежат на кардиоиде . Следовательно, центр масс фигуры, ограниченной кардиоидой , совпадает с центром масс кардиоиды , , положение которого определяется по формуле .

Ответ: x_c = .

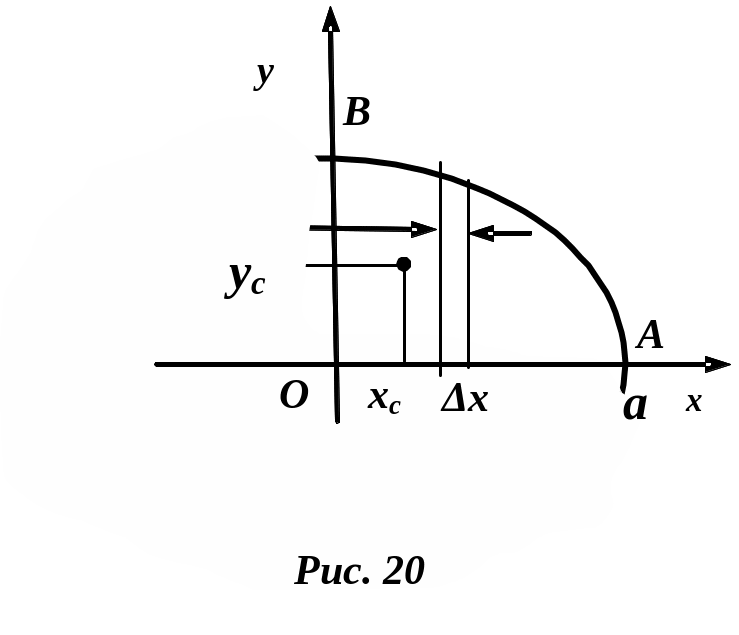
Применение теоремы Гульдена–Паппа к нахождению центра масс плоской фигуры

Рассмотрим плоскую однородную фигуру , ограниченную сверху кривой АВ, которая задана некоторым уравнением , (рис. 20). Поверхностную плотность будем считать постоянной, обозначим ее буквой .

Пусть . Выделим элемент нашей фигуры в виде узкой вертикальной полоски. Предположим, что выделенный элемент представляет собой очень тонкий прямоугольник с основанием и высотой . Тогда получим, что его масса приближенно равна . Центр масс этой полоски приближенно будет находиться в центре прямоугольника на расстоянии от оси и на расстоянии от оси . Для определения соответствующих элементарных статических моментов предположим всю массу полоски сосредоточенной в ее центре масс. Тогда

.

Просуммировав эти элементарные моменты, получим

.

Как и в случае кривой, по этим статическим моментам рассматриваемой фигуры относительно осей координат легко определить координаты центра масс фигуры. Если через обозначить площадь (а, следовательно, и массу) фигуры, то по свойству центра масс

.

Следовательно,

.

Умножив правые и левые части первого соотношения на , получим

.

Справа мы получили объем тела, полученного от вращения плоской фигуры около оси . Слева мы имеем произведение длины окружности, описанной центром масс фигуры на площадь фигуры.Отсюда следует вторая теорема Гульдина–Паппа.

Объем тела вращения плоской фигуры около непересекающей ее оси равен произведению площади этой фигуры на длину окружности, описанной центром масс фигуры:

.

Полученные формулы распространяются на случай, когда фигура ограничена кривыми и сверху и снизу и когда нижний предел интегрирования не равен нулю. В этом случае

.

Пример 1. Найти координату центра масс однородного полукруга (рис. 23).

Решение. Расположим полукруг, как показано на рисунке. Вращая полукруг вокруг оси , получим шар, объем которого равен , где – радиус шара.

Используя теорему Гульдина–Паппа, получим ,

где – площадь полукруга.

Следовательно,

.

Ответ: .

Пример 2. Найти центр масс фигуры, ограниченной ветвью циклоиды (рис. 24).

Решение. Используя теорему Гульдина–Паппа, получим , где – площадь циклоиды. Определим площадь фигуры, ограниченной одной ветвью циклоиды:

.

Далее определим объем тела, полученного вращением ветви циклоиды вокруг оси :

.

Следовательно, .

С помощью теоремы Гульдина-Паппа можно находить также площадь поверхности и объем тел.

Ответ: .

П

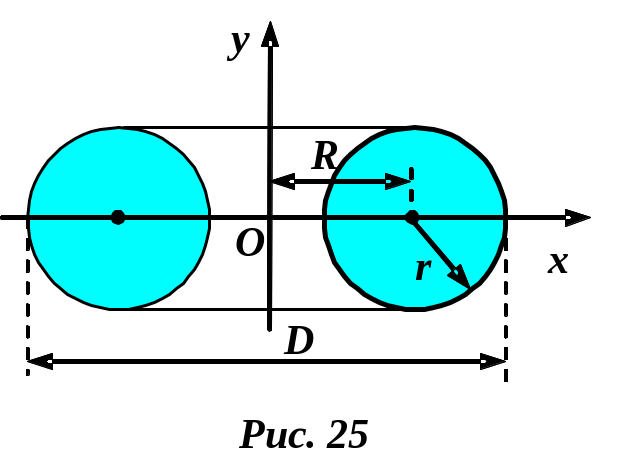
ример 3. Найти площадь поверхности и объем кольца (тора) толщины , внешний диаметр которого равен (рис. 25).

Решение. Представим тор как тело, полученное от вращения вокруг оси окружности радиуса , центр масс которой имеет координату .

Найдем с помощью теоремы Гульдина–Пап­па площадь поверхности и объем полученного тела вращения. Для площади поверхности по первой теореме Гульдина–Паппа имеет место .

Так как , то .

Объем тора вычислим с помощью второй теоремы Гульдина–Папа:

.

Ответ: .

Центр масс пространственных тел

Пример 1. Центр масс конуса (или пирамиды)

В

ычислим центр масс конуса. Для упрощения выкладок рассмотрим конус, обращенный вершиной вниз (рис. 26).

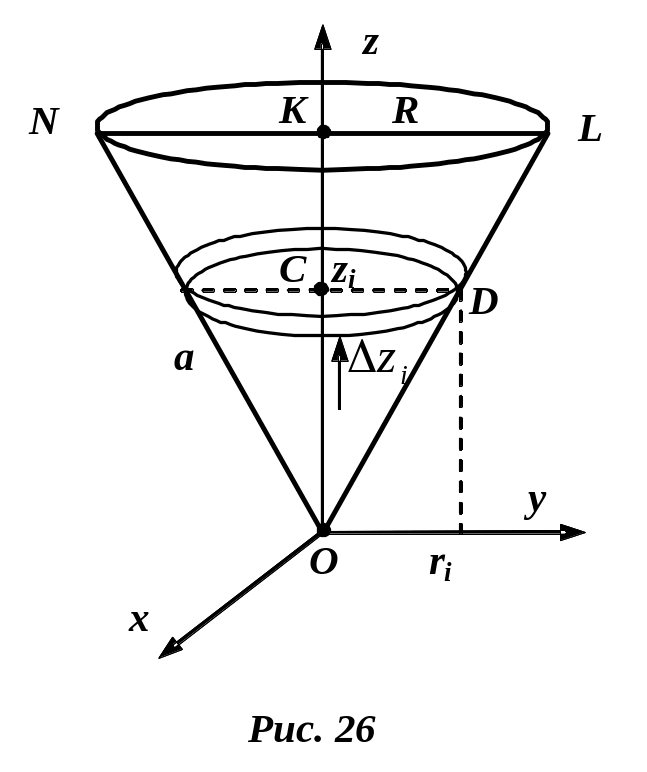
Решение. Определим координату центра масс однородного конуса радиуса , высота которого равна . Выделим тонкий слой на расстоянии от начала координат. Этот слой представляет собой тонкий диск, объем которого будет

.

Из подобия треугольников и имеем . Следовательно, .

Для однородного конуса масса пропорциональна объему, тогда в соответствии с формулой (6)

.

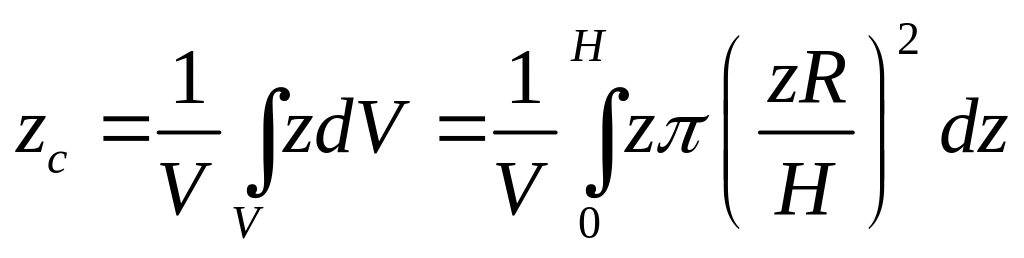Известно, что объем конуса определяется формулой

.

Таким образом,

.

Ответ: .

Этот результат справедлив также для любой многоугольной пирамиды.

Пример 2. Центр масс объема полушара. Определить координату центра масс однородного полушара (рис. 27).

Р

ешение. Так как шар однородный, то для определения координаты его центра масс можно использовать формулу

,

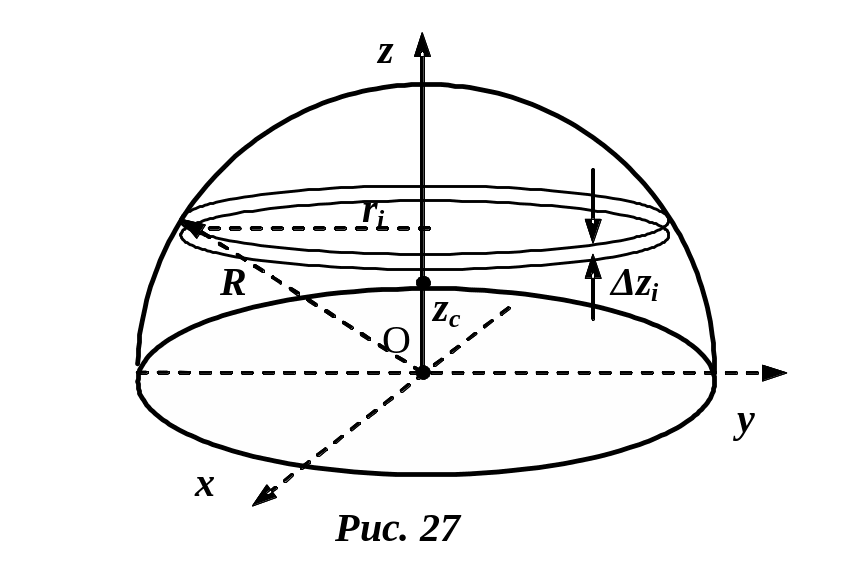
где – радиус полушара, – его объем, .

Выделим в полушаре тонкий горизонтальный диск радиуса и толщины . Его объем определяется соотношением . При этом и .

Следовательно,

.

Ответ: .

Момент инерции плоской кривой

Моменты инерции плоской кривой , относительно координатных осей находится по формуле

,

где – дифференциал дуги.

Если кривая задана параметрически , то

.

Если кривая задана в полярной системе координат , то

.

Пример 1. Момент инерции кольца

П

усть масса кольца – М, радиус – R. Тогда момент инерции кольца относительно оси l, перпендикулярной к плоскости кольца:

Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R.

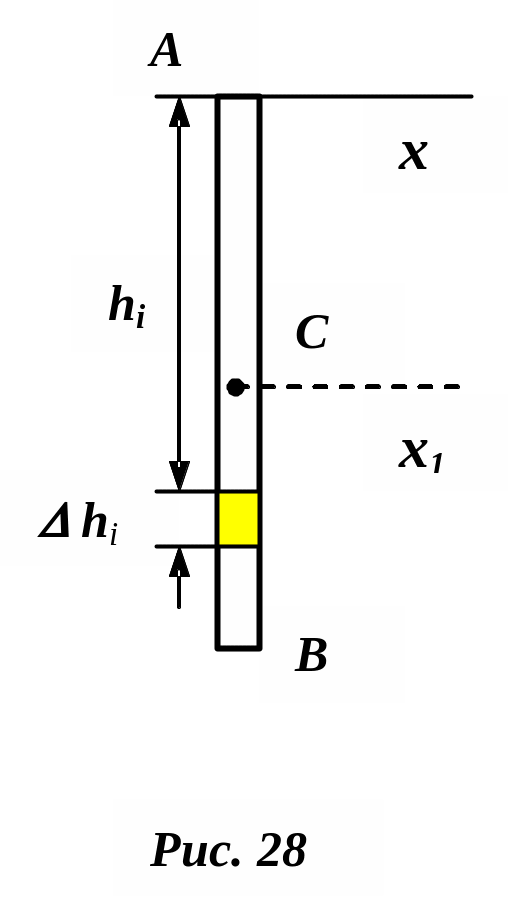
Пример 2. Момент инерции однородного тонкого стержня. Пусть масса стержня М, длина l. Найдем момент инерции относительно оси , перпендикулярной к стержню и проходящей через его конец А (рис. 28). Масса любого элемента стержня будет равна М омент инерции этого элемента относительно оси будет равен

,

где – расстояние выделенного элемента до оси . Суммируя моменты всех элементов стержня и переходя к пределу при , получим выражение момента инерции стержня: .

Если таким же образом вычислить момент инерции относительно оси ,проходящей через центр масс тела С, то получим

Момент инерции плоской фигуры

Проиллюстрируем вычисление моментов инерции плоских фигур на следующих примерах.

Пример 1. Момент инерции однородного сплошного диска

Вычислим момент инерции диска массы М и радиуса R относительно оси , проходящей через центр диска перпендикулярно к его плоскости.

Решение. Разобьем диск на тонкие концентрические кольца. Тогда момент инерции какого-либо из этих колец с радиусом относительно оси l, перпендикулярной к плоскости диска, будет

Для определения массы i-го кольца с радиусом и шириной вычислим его площадь, которая будет пропорциональна его массе

Для малых можно положить . Тогда . Следовательно, масса этого кольца равна

.

Складывая осевые моменты всех колец и переходя к пределу при , мы получим выражение для момента инерции всего диска в виде определенного интеграла

.

Ответ: .

Очевидно, такой же результат получится для момента инерции однородного круглого цилиндра массы М и радиуса R.

Пример 2. Момент инерции квадратной пластины относительно оси, лежащей в плоскости пластины.

В

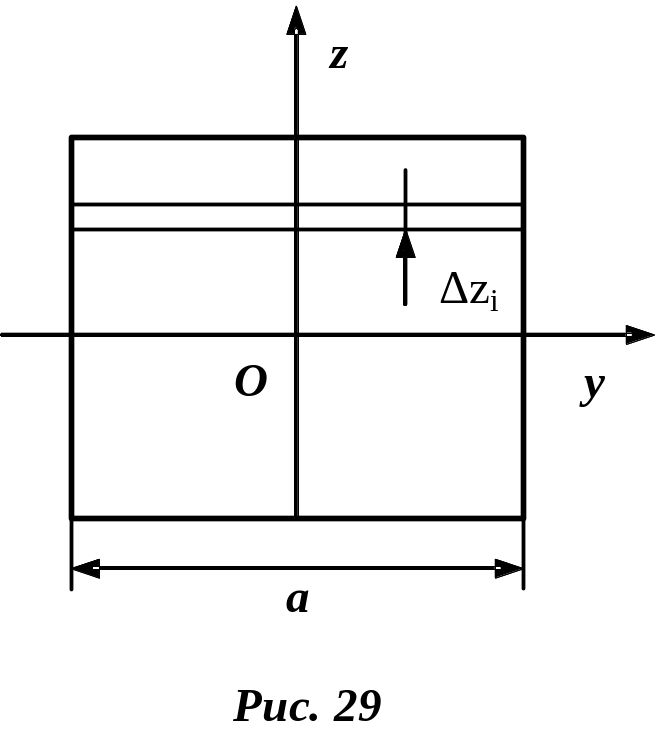
ычислим момент инерции однородной квадратной пластины со стороной относительно оси (рис. 29).

Решение. Выделим тонкий слой на пластинке . Он представляет собой тонкий стержень, момент инерции которого относительно его центра масс, лежащего на оси , будет

где , - плотность пластины.

Момент инерции всей пластины относительно оси получаем по формуле

.

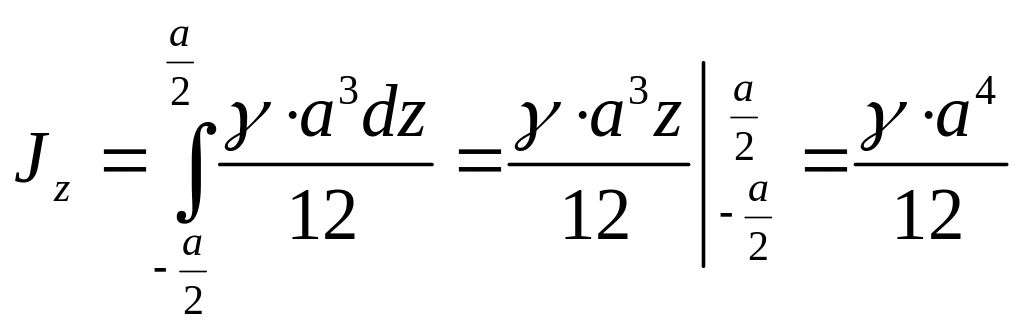Пусть масса всей пластины . Тогда

.

Ответ: .

Пример 3. Момент инерции треугольной пластины относительно оси, лежащей в плоскости пластины.

В

ычислим момент инерции однородной треугольной пластины относительно оси , проходящей через центр масс треугольника (рис. 30).

Решение. Для упрощения расчетов возьмем равносторонний треугольник со стороной . Систему координат выберем так, как показано на рисунке. Выделим тонкий слой на расстоянии от начала координат. Масса выделенного слоя

.

Тогда .

Выразим через . Из треугольника OCD, в котором угол при вершине D равен 60º, получаем . Следовательно . Тогда .

Имеем . Момент инерции всей пластины относительно оси рассчитываем по формуле

.

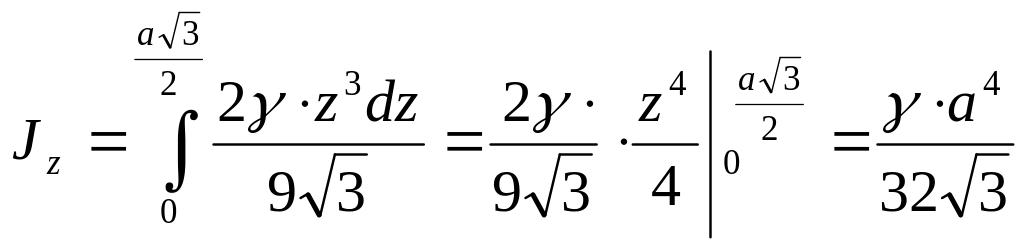Пусть масса всей пластины . Тогда

.

Ответ: .

Аналогично определяется момент инерции относительно оси :

М

омент инерции относительно параллельных осей определяется по формуле Гюйгенса–Штей­нера

,

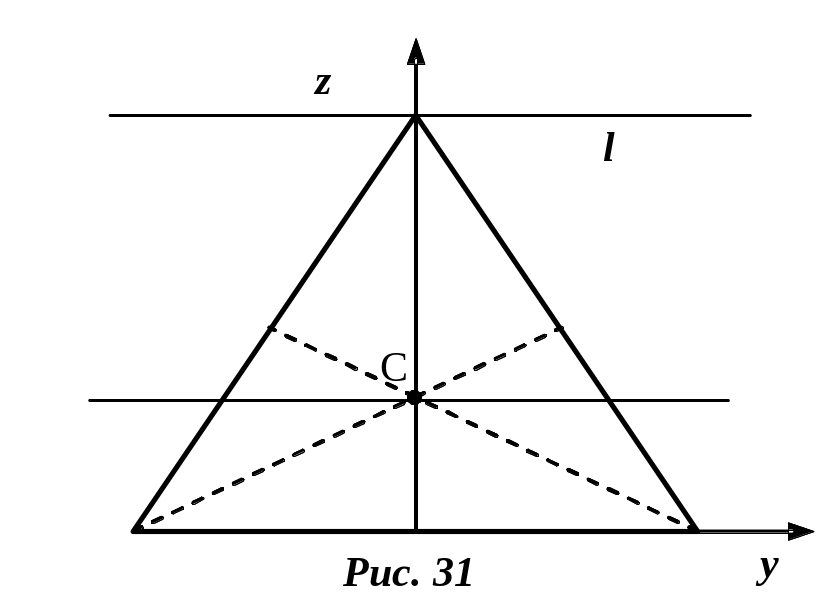
где – момент инерции относительно оси, проходящей через центр масс тела, – момент инерции относительно произ­воль­ной параллельной оси l, d – расстояние между осями, M – масса тела (рис. 31).

В соответствии с формулой Гюйгенса-Штейнера

, где - расстояние между осью и параллельной ей осью, проходящей через центр масс . В нашем примере .

Тогда .

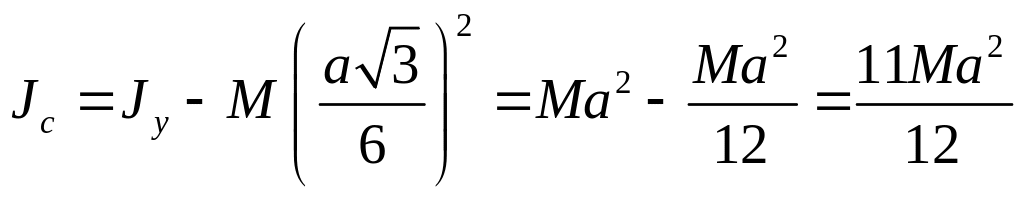Момент инерции относительно оси , параллельной оси и проходящей через вершину треугольника, определяется соотношением .

П

ример 4. Момент инерции квадратной пластины от­но­сительно оси, перпендикулярной плоскости пластины.

Определим момент инерции квадратной пластины относительно оси , перпендикулярной пло­с­кос­ти пластины (рис. 32).

Решение. Выделим тонкий слой на пластинке на расстоянии от начала координат. Масса этого слоя Он представляет собой тонкий стержень, момент которого относительно его центра масс , лежащего на оси , будет

По формуле Гюйгенса-Штейнера момент инерции этого слоя относительно оси будет

.

Момент инерции всей пластины относительно оси получаем по формуле

.

Пусть масса всей пластины . Тогда

.

Ответ: .

Пример 5. Момент инерции треугольной пластины относительно оси, перпендикулярной плоскости пластины.

В

ычислим момент инерции однородной треугольной пластины относительно оси , перпендикулярной плоскости треугольника (рис. 33).

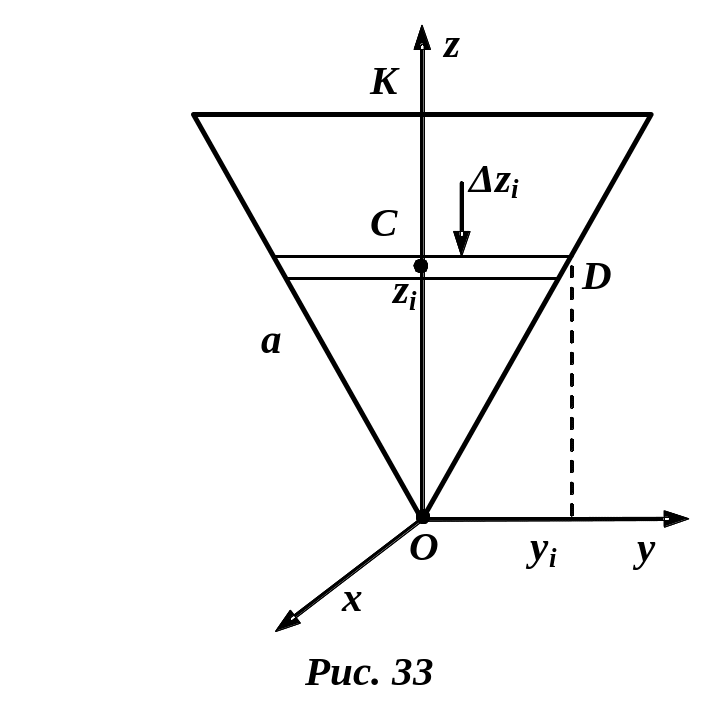
Решение. Для упрощения расчетов возьмем равносторонний треугольник со стороной . Систему координат выберем так, как показано на рисунке. Выделим тонкий слой на расстоянии от начала координат.

Масса выделенного слоя .

Тогда момент инерции выделенного слоя относительно оси, параллельной оси и проходящей через центр масс выделенного слоя будет равен: .

Выразим через . Из треугольника , в котором угол при вершине равен 60⁰, получаем . Следовательно , Тогда .

Момент инерции выделенного слоя относительно оси согласно формуле Гюйгенса-Штейнера будет

.

Имеем . Момент инерции всей пластины относительно оси , проходящей через точку О, получаем по формуле

.

Пусть масса всей пластины . Тогда

.

Ответ:

Момент инерции треугольника относительно оси, проходящей через центр масс треугольника, определяется из соотношения

, .

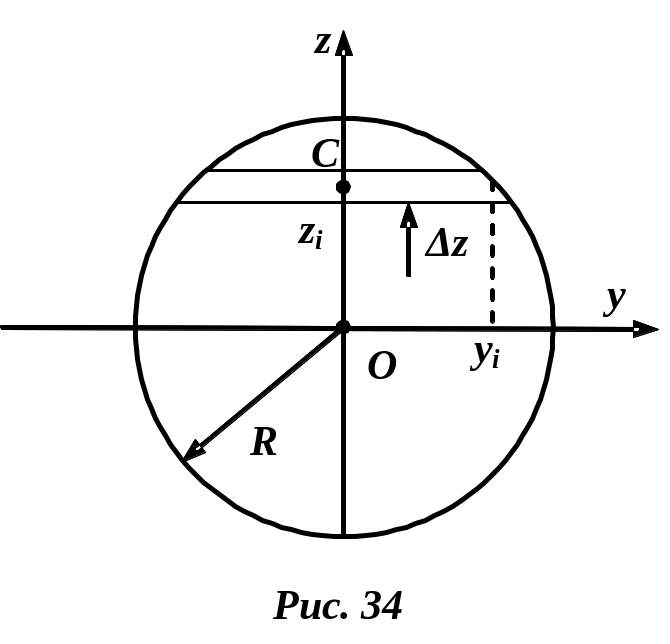
Пример 6. Момент инерции диска относительно оси, лежащей в плоскости диска (рис. 34).

Определим момент и инерции диска относительно оси .

Решение. Выделим тонкий слой на расстоянии от начала координат. Масса выделенного слоя

.Тогда .

Выразим через . Запишем уравнение окружности в параметрическом виде .

Следовательно,

.

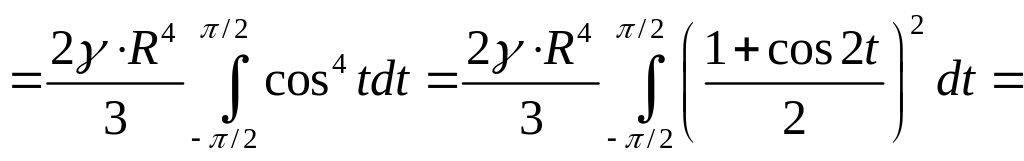
Пусть масса диска . Тогда

Ответ: .

Моменты инерции пространственных тел

Пример 1. Момент инерции однородного куба относительно координатных осей, проходящих через центр масс куба.

Вычислим момент инерции куба массы со стороной относительно оси (рис. 35).

Р

ешение. Выделим тонкий слой . Его масса .

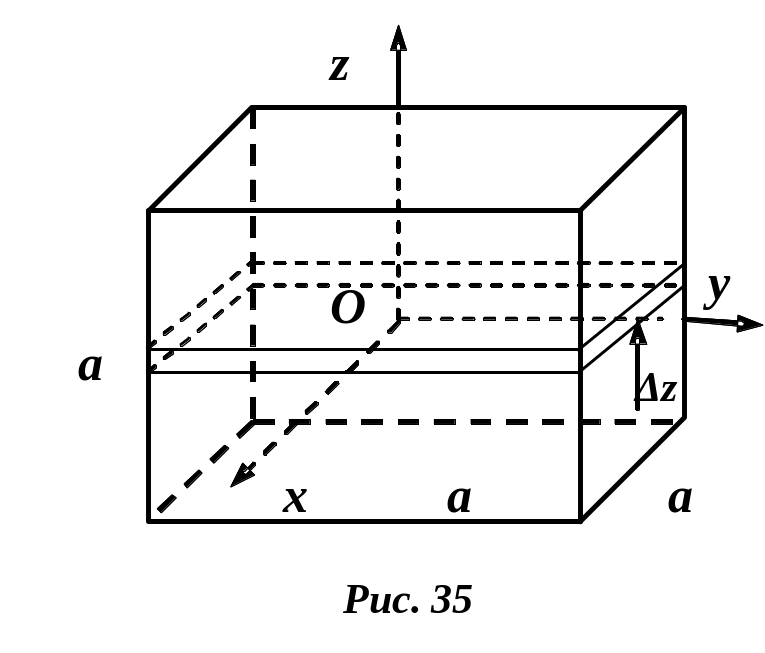
Момент инерции выделенного слоя, представляющего собой квадрат со стороной , относительно оси равен

.

Момент инерции всего куба относительно оси , проходящей через центр масс куба:

.

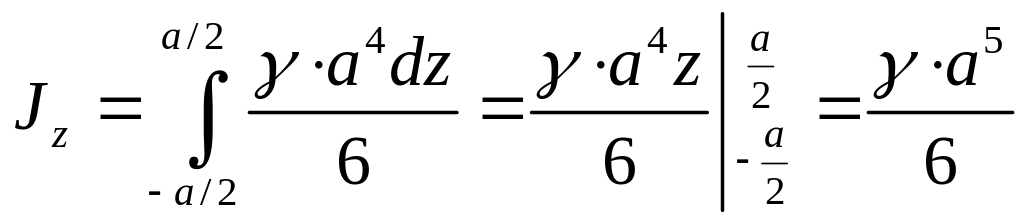Пусть масса куба , тогда .

Ответ: .

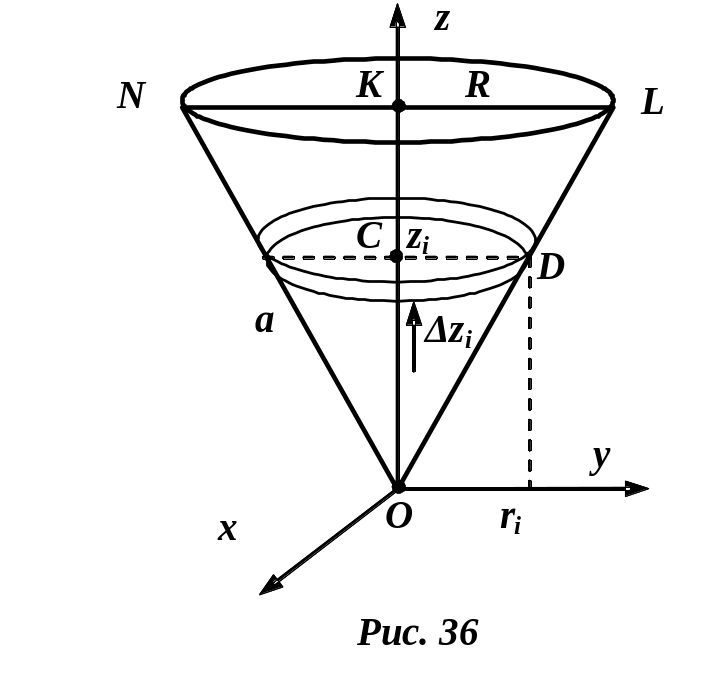
Пример 2. Момент инерции конуса относительно оси вращения (рис. 36).

Определим момент инерции конуса радиус основания которого , а в сечении - правильный треугольник.

Р

ешение. Выделим тонкий слой на расстоянии от начала координат. Этот слой представляет собой тонкий диск, масса которого . Тогда .

Выразим через . Из треугольника , в котором угол при вершине равен 60º, получаем .

Следовательно, , .

Имеем . Момент инерции всего конуса относительно оси вращения получаем по формуле:

.

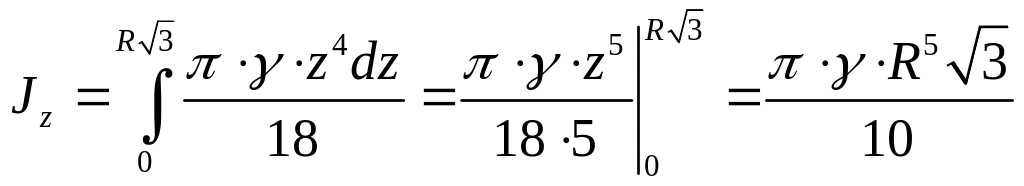Пусть масса всего конуса . Тогда

.

Ответ: .