2.4. Вычисление площади поверхности вращения

1) Если дуга кривой, заданная уравнением , вращается вокруг оси , то площадь поверхности вращения вычисляется по формуле:

,

где – абсциссы начала и конца дуги.

2) Если дуга кривой, заданная уравнением , вращается вокруг оси , то

,

где – ординаты начала и конца дуги.

3) Если дуга кривой задана параметрическими уравнениями , то

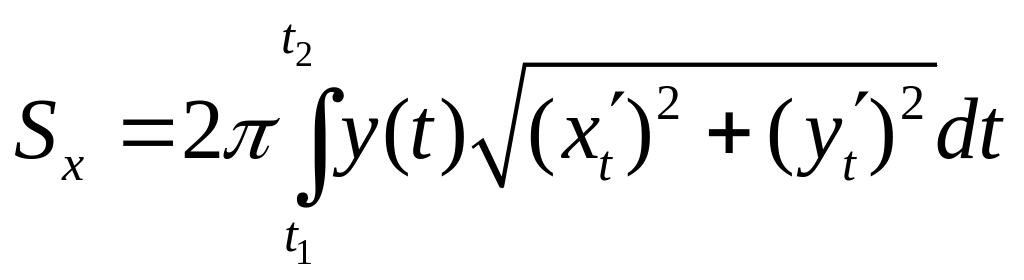. (4)

4) Если дуга задана в полярных координатах , то

.

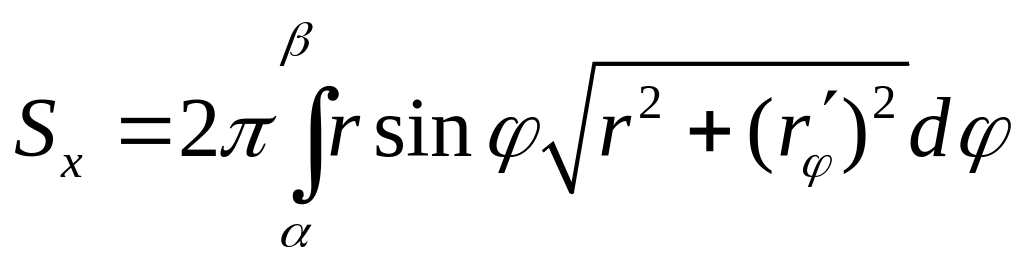Пример. Найти площадь поверхности, образованной вращением астроиды вокруг оси (рис.11).

Решение. В силу симметрии полученной поверхности достаточно посчитать половину площади. В соответствии с формулой (4) получим

,

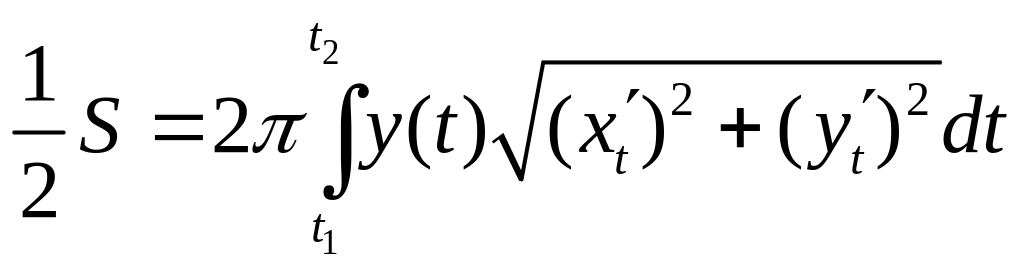где .

Имеем ,

.

Тогда

.

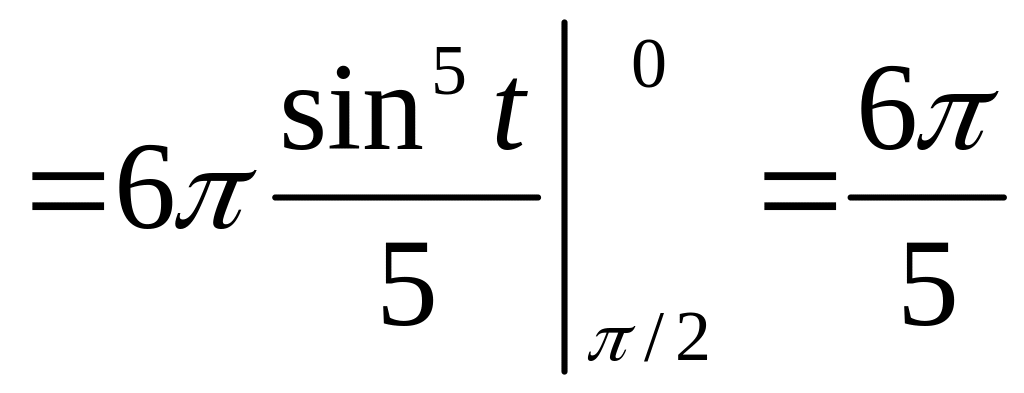Ответ: .

3. Механические приложения определенного интеграла

1. Работа переменной силы

Работа переменной силы, заданной функцией и направленной вдоль оси на отрезке , равна интегралу:

.

Пример. Определить работу А, которую необходимо затратить на выкачивание воды из резервуара, представляющего собой цилиндр радиуса , длины (рис. 12). Удельный вес воды принять равным

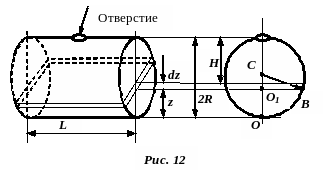
Решение. На высоте выделим слой воды .

Его объем

.

Этот слой нужно поднять на высоту . Элементарная работа , затраченная на выкачивание слоя , определяется по формуле

.

Работа А по выкачиванию всей воды равна сумме всех элементарных работ:

.

Вычислим полученный интеграл, представляющий собой дифференциальный бином, для которого

.

Так как , то для вычисления интеграла воспользуемся подстановкой .

Имеем

.

Если , то , если , то .

Следовательно,

.

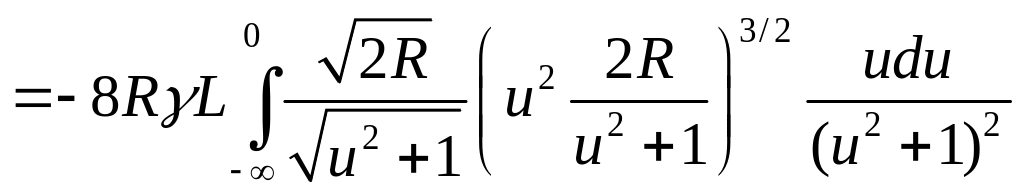После некоторых преобразований получим

.

Подынтегральная функция в последнем интеграле является правильной рациональной дробью, которую можно разложить в сумму простейших дробей.

Сделаем замену переменных .

Тогда

,

или

.

Приравнивая коэффициенты при равных степенях справа и слева, получим

.

Следовательно,

∙ du =

.

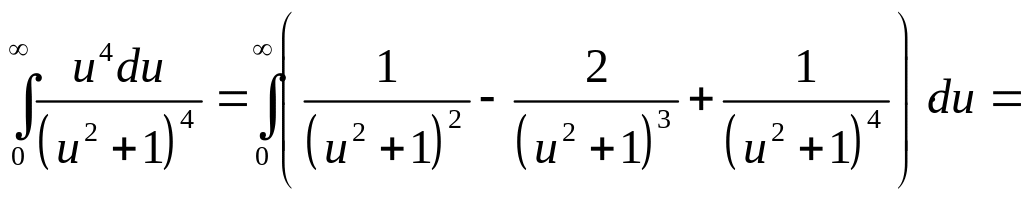
Для вычисления полученных трех интегралов воспользуемся рекуррентной формулой

.

Тогда

.

Аналогично получим

.

Таким образом,

.

Если то .

Ответ: Если то А = 157 ед.

3.2. Давление жидкости на пластину

П

ример. Треугольная пластина с основанием м и высотой м погружена вертикально вершиной вниз в жидкость так, что основание параллельно поверхности жидкости и находится на расстоянии м от поверхности (рис. 13). Плотность жидкости т/м³. Вычислить силу давления жидкости на каждую из сторон пластины.

Решение. Для определения силы давления жидкости на пластину воспользуемся законом Паскаля, согласно которому давление жидкости на площадку , погруженную на глубину равно: , где – плотность жидкости, – ускорение свободного падения.

Прямыми, параллельными поверхности жидкости, разобьем треугольник на элементарные полоски шириной , отстоящие от поверхности жидкости на расстоянии . Из подобия треугольников и имеем:

,

т.е. площадь вырезанной полоски

.

Давление на каждую из сторон полоски треугольной пластины:

.

Интегрируя обе части последнего равенства, получаем:

кН.

Ответ: Р ≈ 44,1 кН.