Пример. Вычислить длину дуги отрезка цепной линии.

Решение. Цепной называется линия, форму которой принимает тяжелая нить, закрепленная в двух точках (рис. 7). Уравнение цепной линии может быть записано в виде

,

где – параметр цепной линии.

Э

то уравнение про­ще записать в следующем виде

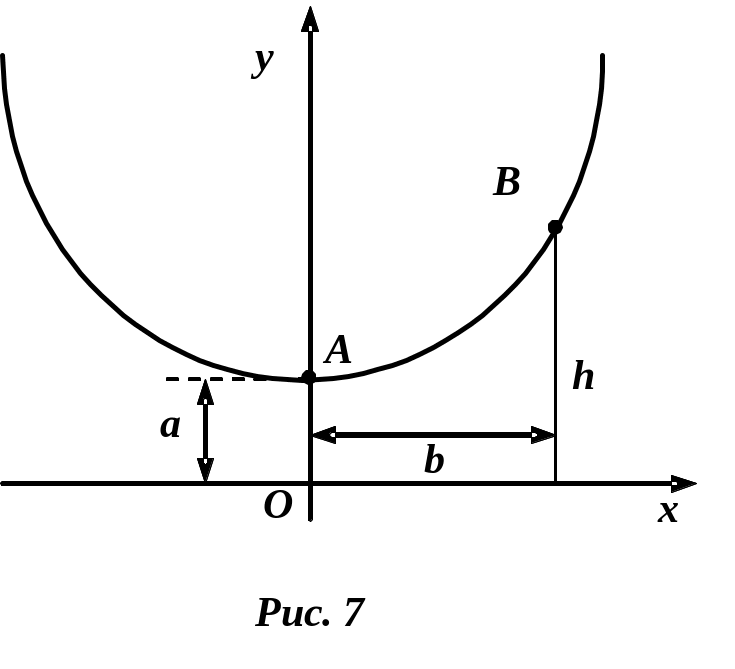
, (1)

где – гиперболический косинус.

Точка является наиболее низкой точкой кривой. Она называется вер­шиной цеп­ной линии. Вычислим длину дуги АВ.

Пусть точка В имеет координаты . Дифференцируя уравнение (1), будем иметь ,

.

Следовательно, . Отсюда согласно формуле получим длину дуги АВ:

.

Эту формулу можно упростить, подставив в формулу (1) вместо ординату точки в. Получим . Из известной формулы имеем

.

Ответ: l = .

Параметрическое задание кривой

Пусть кривая задана параметрически системой уравнений .

Тогда длина кривой определяется по формуле

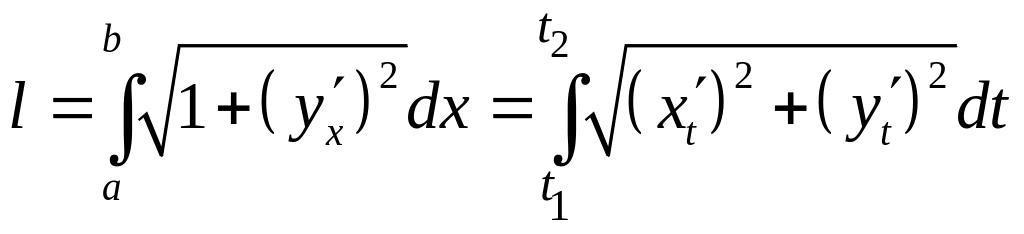, . (2)

Здесь использовалось соотношение

.

Пределы интегрирования пересчитываются по формулам:

1) ; 2) .

Пример 1. Определить длину окружности радиуса R.

Решение. Пусть уравнение окружности имеет вид

.

Вычислим длину части окружности, лежащей в первой четверти. Согласно формуле

, где , .

Таким образом,

=

.

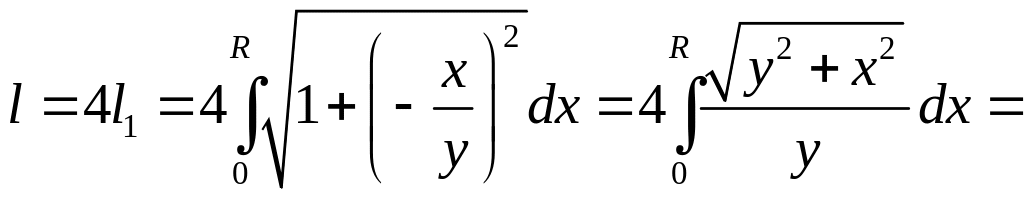
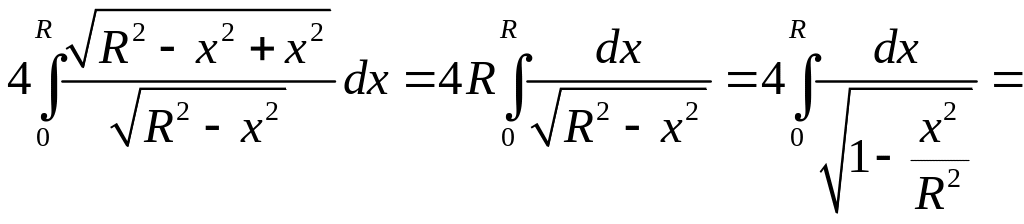
Запишем уравнение этой окружности в параметрическом виде . Найдем , – часть окружности, лежащая в первой четверти. По формуле (2), получим

.

Начальное и конечное значения параметра t: .

Ответ: .

Пример 2. Вычислить длину дуги линии, заданной параметрически

от начала координат до ближайшей точки с вертикальной касательной.

Решение. Линия задана параметрически, так как интеграл с переменным верхним пределом есть функция от t. Производная от интеграла по переменному верхнему пределу равна подынтегральной функции, вычисленной при значении аргумента, равном верхнему пределу (от подынтегральной функции требуется непрерывность):

.

Найдем точку пересечения данной линии с вертикальной касательной , где

Касательная параллельна оси , следовательно, ее угловой коэффициент равен нулю, . Так как , то , а, следовательно, , , .

Нас интересует ближайшая точка с вертикальной касательной. Тогда . Определим значение параметра в начале координат, т.е. в точке . Так как следовательно, , что выполняется при условии равенства пределов интегрирования, т.е. .

Используя формулу (2) длины кривой, заданной параметрически, получим;

.

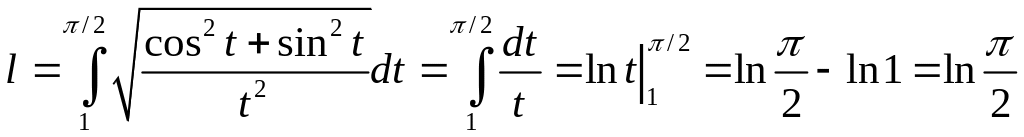Полярные координаты

Пусть кривая задана уравнением в полярных координатах . Перейдем к декартовым координатам

.

Это уже уравнение кривой в параметрическом виде. Имеем

,

где . Подставив полученные соотношения в формулу для параметрически заданной кривой, получим

.

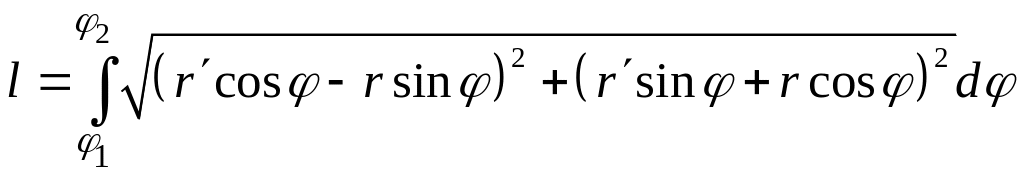После некоторых преобразований будем иметь

.

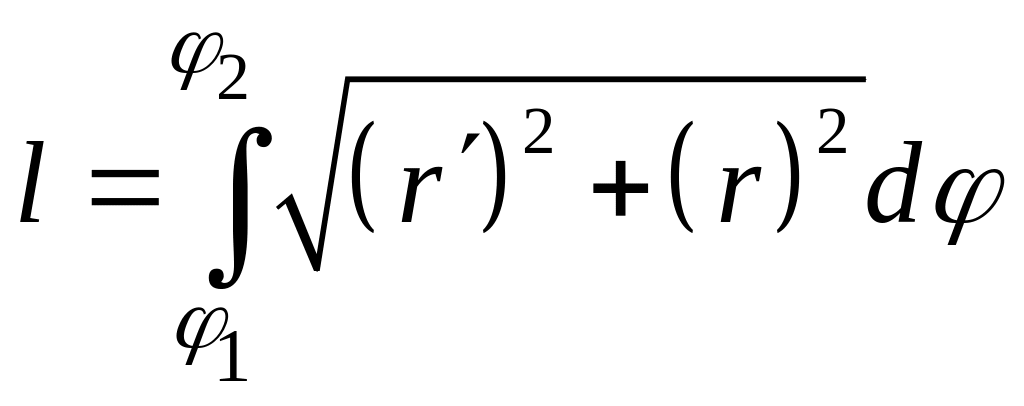Пример. Найти длину кардиоиды (рис. 8).

Р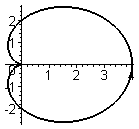 ешение. Вычислим

,

, .

Подставим в формулу для

Рис. 8 длины дуги, получим

=

.

Ответ: .

2.3. Вычисление объемов

Объем тела по известным площадям поперечных сечений

П усть в пространстве задано тело и построены его сечения плоскостями, пер­пен­дикулярными оси и проходящими через точки на ней (рис. 9). Площадь фигуры, образующейся в сечении, зависит от точки , определяющей плоскость сечения. Предпо­ложим, что эта зависимость известна и задана непрерывной на отрезке функцией . Тогда объем тела, находящегося между плоскостями , вычисляется по формуле

Объемы тел вращения

Прямоугольная система координат

Пусть вокруг оси вращается криволинейная трапеция, ограниченная графиком функции . В этом случае объем тела вращения вычисляется по формуле

. (3)

Если тело получено от вращения криволинейной трапеции вокруг оси , то объем тела вычисляется по формуле

.

Пример. Вычислить объем тела, образованного вращением криволинейной трапеции, ограниченной линиями вокруг оси (рис. 10).

Решение. В соответствии с формулой (3) имеем

=

.

О

Рис.10

твет: .

Параметрическое задание

Если кривая задана параметрически , то объем тела вращения вычисляется по формулам:

,

,

где – значения параметра начала и конца дуги кривой. Для 1-й формулы – значение находится из уравнения , значение – из уравнения . Для 2-й формулы – значения находится из уравнения ; значение – из уравнения .

Пример. Найти объем тела, полученного от вращения астроиды вокруг оси (рис. 11).

Р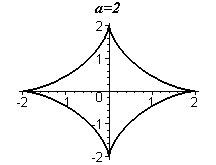 ешение. Имеем .

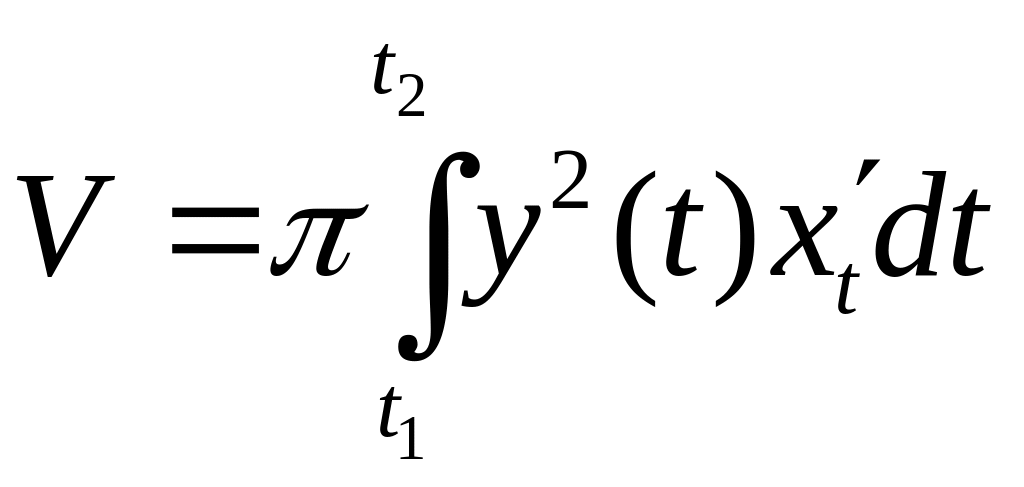Определим значения . Посчитаем половину объема тела вращения. В этом случае координата меня-

ется от до .

Рис.11 Если , то

.

При получим .

Следовательно,

.

Ответ: .

Полярная система координат

В случае полярной системы координат вращаемая кривая задается уравнением . Объем тела, полученного вращением сектора, ограниченного дугой и двумя полярными радиусами вокруг полярной оси, может быть вычислен по формуле

.

Этой же формулой удобно пользоваться при отыскании объема тела, полученного вращением вокруг полярной оси фигуры, ограниченной замкнутой кривой, заданной в полярной системе координат.

Пример. Найти объем тела, полученного от вращения окружности вокруг оси .

Решение. Имеем

.

Ответ: .