Порівняння двох дисперсій нормальних гс

Отримані незалежні вибірки, обсяги яких n₁ , n₂ , що добуті із нормальних генеральних сукупностей.

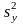Правило 1. Для того, щоб при заданому рівні значущості  і знайдених виправлених вибіркових дисперсій і перевірити нульову гіпотезу H₀: про рівність генеральних дисперсій D (X) = D (Y) при конкуруючій гіпотезі H₁: D (X)  D (Y), потрібно попередньо визначити більше та менше значення виправлених вибіркових дисперсій, а потім обчислити спостерігаєме значення критерію Фішера-Снедекора F_сп = 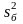/ і за таблицею критичних точок Фішера-Снедекора, по заданому рівню значущості  і числам ступенів вільності k₁ = n₁ –1, k₂ = n₂ – 1(відповідно для , ), знайти критичну точку F_кр (, k₁, k₂ ) правосторонньої області. Якщо F_сп  F_кр – немає підстав відкинути нульову гіпотезу H₀, а якщо F_сп  F_кр – гіпотезу H₀ відкидають (відхиляють).

________________________________0____________F_кр////////////////////////////////////////////

Правило 2 (для двохсторонньої критичної області). При конкуруючій гіпотезі H₁: D (X)  D (Y) критичну точку F_кр (/2, k₁, k₂ ) шукають за рівнем значущості /2 і числам ступенів вільності k₁ і k₂ (де k₁ – число ступенів вільності більшої дисперсії). Якщо F_сп  F_кр – немає підстави відкинути нульову гіпотезу H₀ про рівність генеральних дисперсій D (X) = D (Y), а якщо F_сп  F_кр – гіпотезу H₀ відкидають.

///////////////////////////////(-F_кр)____________0______________F_кр/////////////////////////////////////

Порівняння виправленої вибіркової дисперсії s² з гіпотетичною генеральною дисперсією 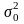нормальної сукупності.

За вибіркою, обсягом n знайдено виправлена дисперсія s².

Правило 1. Для того, щоб при заданому рівні значущості , перевірити нульову гіпотезу H₀: ² = про рівність невідомої генеральної дисперсії ² гіпотетичному (припускаємому) значенню при конкуруючій гіпотезі H₁: ²  , потрібно обчислити спостерігаєме значення відомого критерію Пірсона (“хі квадрат”) 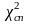= (n –1) s² / і за таблицею критичних точок розподілу ², за заданим рівнем значущості  і числу ступенів вільності k = n –1 знайти критичну точку (, k ). Якщо  – немає підстави відкинути нульову гіпотезу H₀. Якщо  – нульову гіпотезу відкидають.

Правило 2. При конкуруючій гіпотезі H₁: ²  знаходять ліву (1– /2, k) і праву 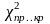( /2, k) критичні точки. Якщо < < – немає підстави відкинути нульову гіпотезу H₀. Якщо < або > – нульову гіпотезу відкидають.

Правило 3. При конкуруючій гіпотезі H₁: ² < знаходять критичну точку (1– ; k). Якщо > (1– ; k) – немає підстави відкинути нульову гіпотезу H₀. Якщо < (1–; k) – нульову гіпотезу відкидають. Якщо число ступенів вільності k > 30, то критичну точку (; k) можна знайти із рівності Уілсона-Гільферті: (; k) = k 1– 2/9k + z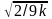_ ³ , де z_ знаходять, використовуючи функцію Лапласа  (t), із рівності  (z_)=(1 – 2) /2.

Порівняння двох середніх генеральних сукупностей, дисперсії яких відомі (великі незалежні вибірки).

Відомі обсяги великих незалежних вибірок (n > 30, m > 30), за якими знайдені відповідні вибіркові середні і . Генеральні дисперсії D (X) і D (Y) відомі.

Правило 1. Для того, щоб при заданому рівні значущості , перевірити нульову гіпотезу H₀: M (X) = M (Y) про рівність математичних сподівань (генеральних середніх) двох нормальних генеральних сукупностей з відомими дисперсіями, при конкуруючій гіпотезі H₁: M (X)  M (Y) , потрібно обчислити спостерігаєме значення критерію Z_сп = ( – ) / і за таблицею функції Лапласа знайти критичну точку z_кр із рівності  (z_кр ) = (1 – ) / 2. Якщо < z_кр – немає підстави відкинути нульову гіпотезу H₀. Якщо > z_кр – нульову гіпотезу відкидають.

Правило 2. При конкуруючій гіпотезі H₁: M (X) > M (Y) знаходять критичну точку z_кр за таблицею функції Лапласа із рівності  (z_кр ) = (1 – 2) / 2. Якщо Z_сп < z_кр – немає підстави відкинути нульову гіпотезу H₀. Якщо Z_сп > z_кр – нульову гіпотезу відкидають.

Правило 3. При конкуруючій гіпотезі H₁: M (X) < M (Y) знаходять “допоміжну точку” z_кр за правилом 2. Якщо Z_сп > -z_кр – немає підстави відкинути нульову гіпотезу H₀. Якщо Z_сп < -z_кр – нульову гіпотезу відкидають.