Властивості m (X) для двв і для нвв:

M (С) = С, де С = const;

M (X₁ + X₂+…+ X_n) = M (X₁) + M (X₂) + …+ M (X_n);

M (X₁  X₂  … X_n) = M (X₁)  M (X₂) … M (X_n);

Математичне сподівання біноміального розподілу:

M (X) = n  p,

де n – число випробувань, p – імовірність появи події в одному випробуванні.

Для НВВ X  (-, ) або X  [а, в ], диференціальна функція якої f (x) маємо відповідно:

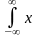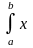M (X) = f(x) dx; M (X) = f(x) dx.

Можна довести, що для X, заданої диференціальною функцією f (x)  0 на відрізку [а, в], а зовні відрізку f (x) = 0, виконується а  M (X)  в.

Генеральна дисперсія (розсіяння, розкид) D_г випадкової величини X – математичне сподівання квадрату відхилення:

D_г  D (X) = M [X – M (X)]²  M (X²) – [M (X)]² ; D (X) =

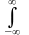= (x – M (X))²f (x) dx  x²f (x) dx – [M (X)]² ;

D (X) = 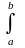(x – M (X))²f (x) dx,

де можливі значення X  (–, ) або X  (а, в).

Властивості дисперсії:

D (X)  0; D (С) = 0; D (СX) = С²D (X); D (X Y) = D (X) + D (Y),

де X і Y – довільні незалежні випадкові величини. Розмірність (Dim) дисперсії дорівнює квадрату розмірності X. Дійсно, якщо X – випадкова сила F, то Dim X  Dim F = Н (Ньютон), то D (X) має розмірність Dim D (X) = Dim M [X – M (X)]² = Н². Ось чому уводиться поняття – середнє квадратичне відхилення

 (X) = 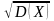, де ² = D_г.

Теоретичний початковий момент порядку k випадкової величини X – математичне сподівання величини X^k:

_k = M (X^k).

Зокрема, початковий момент першого порядку

₁ = M (X).

Центральний момент порядку k випадкової величини X – математичне сподівання величини: [X – M (X)]^k :

_k = M [ X – M (X)]^k.

Зокрема, ₁ = M [ X – M (X)] = 0,

₂ = M [ X – M (X)]² = D (X); ₂ = ₂ – .

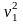Для НВВ:

_k = x^k f (x) dx ; _k = (x – M (X))^k f (x) dx .

Інші характеристики НВВ X:

Мода Мo(X) можливе значення x₀  X, якому відповідає max диференціальної функції f (x).

Медіана Мd(X) – те можливе значення x_e  X, яке визначається рівністю:

P (X < М_e(X)) = P (X > М_e(X)).

Іншими словами, медіана тлумачиться як точка x_e, в якій ордината f (x_е) поділяє наполовину площу, яка обмежена кривою розподілу.

Числові характеристики деяких законів розподілу

(більш детально і глибоко про це та інше є в [12]).

2.1. Рівномірний розподіл f (x) = 1/(в – а), X  (а, в). M (X)=(а + в)/2;D (X)=(в – а)²/12;  (X)=(в – а)/2 .

2.2. Розподіл Лапласа f (x) = 0,5 exp 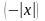, X  (-, ) . M (X) = 0.

2.3. Показниковий розподіл f (x) =  exp (–x), x  0. M (X) = 1/ ; D (X) = 1/ ²;  (X) = 1/ .

2.4. Біноміальний розподіл P_n(k) =  p^k  q^n-k . M (K) = 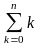P_n(k) = np; D (K) = npq.

2.5. Розподіл Пуассона P_n(k) = ( ) / k! , = np = const, де  –параметр розподілу. M (K) = D (K) = .

2.6. Нормальний розподіл N (m, ²)  f (x) = 1/( )  exp – ,

де  (X) = , D (X) = ². M (X) = m.

Значення аргументу x = m відповідає max функції f (x) – густини ймовірностей; очевидно, при x = m похідна = 0, при x  m похідна  0, при x  m похідна  0, таким чином, точка x = m є точкою максимуму. За визначенням моди М₀(X) = m. Симетричність графіку функції f (x) відносно прямої x = m дозволяє стверджувати, що медіана М_e(X) = m. Таким чином, мода і медіана нормального розподілу співпадають з математичним сподіванням:

M (X) = М₀(X) = М_e(X) = m.

Нормалізований розподіл буде при

параметрах m = 0 та  =1 і має вигляд:

N (0, 1)  f (x) = 1/( )  exp (– x²/2).