
- •1. Завдання до лабораторної роботи
- •2. Вимоги до оформлення звіту
- •3. Основні теоретичні відомості
- •4. Формати використання функцій fsolve та step
- •Варіанти завдань до лабораторної роботи.
- •Варіанти схем об’єктів моделювання
- •Приклад виконання роботи
- •1. Завдання (варіант 13).
- •2. Побудова математичної моделі.
- •Або в іншому вигляді
- •3. Визначення невідомих параметрів стану рівноваги.
- •3.1. За аналітичними залежностями .
- •3.2. Числовими методами.
- •4. Лінеаризація математичної моделі.
- •5. Дослідження реакції моделі на стрибкоподібне збурення.
- •Порівняння графіків перехідних процесів, отриманих для нелінійної та лінійної моделей.
- •7. Висновки
- •Контрольні запитання
Варіанти схем об’єктів моделювання
1) 2)
2)
3) 4)
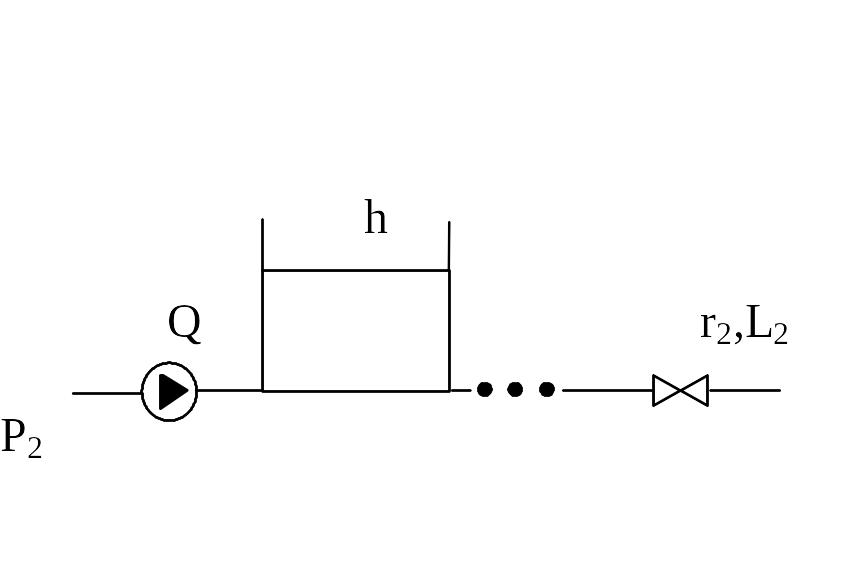
4)
5) 6)
6)
7) 8)
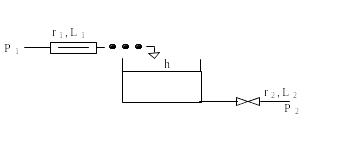
8)
9) 10)
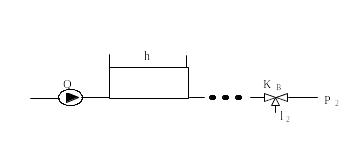
10)
 12)
12)
ДОДАТОК 2
Приклад виконання роботи
1. Завдання (варіант 13).
Побудувати та дослідити математичну модель відкритої проточної гідравлічної ємності, зображеної на малюнку.
Значення конструктивних параметри:
d=0.5м, r1=0.06м, L1=4м, r2=0.14м, L2=110м, kВ=1е-02м2, =0.9;
Номінальні значення:
вхідних величин: P1=40кПа,
P2=0.2кПа;
керування: l2=0.3;
Значення стрибкоподібно зміненої вхідної величини: P1=25 кПа.
2. Побудова математичної моделі.
Згідно з рівнянням збереження маси речовивни та ввівши деякі припущення (масообмін на границі розділу фаз рідина-повітря відсутній, =const ), запишемо диференційне рівняння, що описує зміну рівня в ємності
![]() .
(1)
.
(1)
де S=d2/4 - площа ємності, м2;
h - рівень рідини в ємності, м;
Q - об’ємна витрата, м3/c.
Витрата в першому трубопроводі з турбулентним режимом течії визначається на основі закону Дарсі-Вейсбаха:
 .
(2)
.
(2)
Зміна витрати в другому трубопроводі описується диференційним рівнянням:
 ,
(3)
,
(3)
де
 ,
,
g - прискорення земного тяжіння, g=9.8 м/с2.
Рівняння (1), (2), (3) складають систему нелінійних диференційних рівнянь, що описують об’єкт моделювання:
 (4)
(4)
Або в іншому вигляді
![]() (5)
(5)
Як видно з (5), параметри стану об’єкту - це рівень h та витрата рідини Q2 в другому трубопроводі. Нехай для даної проточної ємності зовнішнім об’єктом буде регулятор рівня рідини в ємності. Тоді, вихідною величиною об’єкту є рівень в ємності h.
3. Визначення невідомих параметрів стану рівноваги.
3.1. За аналітичними залежностями .
Параметрами стану для даного об’єкту
є величини
![]() та h. В стані рівноваги
=
та h. В стані рівноваги
=![]() =
const, h=h0= const. Враховуючи
це, перепишемо систему (5) для стану
рівноваги
=
const, h=h0= const. Враховуючи
це, перепишемо систему (5) для стану
рівноваги
![]() (6)
(6)
Із (6)
![]() .
(7)
.
(7)
Якщо позначити
 і
підставити (7) в друге рівняння системи
(6), то одержимо
і
підставити (7) в друге рівняння системи
(6), то одержимо
![]() ,
,
звідки
 .
(8)
.
(8)
Значення h0 та
![]() ,
зручно знайти, описавши вирази (7), (8) в
script-файлі. Наприклад, в даному варіанті
початкові значення параметрів стану
отримано при виконанні програми,
записаної у script-файлі pu1.m:
,
зручно знайти, описавши вирази (7), (8) в
script-файлі. Наприклад, в даному варіанті
початкові значення параметрів стану
отримано при виконанні програми,
записаної у script-файлі pu1.m:
% Файл розрахунку початкових значень параметрів
% за аналітичними залежностями
ro=1000; g=9.8; dz=0.9; kv=1e-2;
d=0.5; r1=0.06; L1=4; r2=0.14; L2=110;
l=0.3; p1=40000; p2=200;
% -------------------------------------------------
k2=sqrt(4*pi^2*r2^5/(L2*dz));
k1=sqrt(4*pi^2*r1^5/(L1*dz));
B=1+(k2/kv/l)^2;
% -------------------------------------------------
disp( 'Початкові значення параметрів' )
h0=(B*k1^2*p1+k2^2*p2)/(B*k1^2+k2^2)/ro/g
Q20=k1*sqrt((p1-ro*g*h0)/ro)
Результати виконання програми:
h0 = 2.3498, Q20 = 0.0120
