1(17).Способы задания графов. Потоки на сетях. Алгоритмы Форда-Фалкерсона. Граф – совокупность множеств Х и U обозначают G=(Х,U). Х – вершины графа, (изобр. точками пло-ти, пр-ва). U содержит элементы пары связанных элементов мн-ва Х ( изобр. отрезками прямых или кривых линий). Если в паре хi, xj указано направление их связи, то соединяющий их отрезок называют дугой, иначе ребром. If в графе все эл-ты мн-ва U дуги, то граф ориентированный (ор-граф). Графы, в которых мн-ва Х и U конечные (содержат конечное число элементов) наз. конечными. Вершины смежные, если они различны и сущ. дуга, соед-щая эти вершины. Если две дуги имеют общую концевую точку - смежные. Степенью вершины P(Xi) наз. кол-во дуг (ребр) инцидентных дан. вершине, вершина степ. 0 – изолированная. Полустепень захода Хi - кол-во дуг входящих в эту вершину P+(Xi. P+(Xi)+ P-(Xi)= P(Xi).Граф простой, если он не содержит петель и параллельных дуг (ребр). Простой граф, в котором каждая пара вершин смежная называется полным. Граф содержащий хотя бы 2 параллельные дуги (ребра) – мульграф. Путем в ор-графе называется последовательность дуг, в которой конец каждой предыдущей совпадает с началом следующей. В неориентированном графе последовательность ребер, в которой каждые два соседних ребра смежные называют путем. Путь, у которого начальная и конечная вершины совпадают – цикл. Если концевые вершины совпадают то дугу назыв. петлей. Неориентированный граф связный, если любые 2 его вершины можно соединить путем (иначе несвязный). Обычно дугам (ребрам) графа сопоставляют какие-либо числовые характеристики, которые называют весами. Граф G с весами на дугах (ребрах) взвешенный.

Способы задания графов. Графу G {mxn} можно сопоставить матрицу инциденций. mxn, строки которой соответствуют вершинам графа, а столбцы дугам. Элементы матрицы rij:{0;1;-1} -1 -дуга выходит из соответствующей вершины; 1 - входит в вершину; 0 -дуга не инцидентна вершине. неориентированный - {0,1}. Для любого графа G можно определить матрицу смежности вершин. Матрица nxn, в которой строки и столбцы соответствуют вершинам графа. Каждый элемент матрицы равен числу дуг идущих из i вершины в j. Если граф неориентированный, то матрица будет симметричной. Говорят, что одна дуга предшествует другой, если конец первой дуги является началом второй. Графу G можно задать с помощью матрицы смежности дуг ( ребр). Это матрица mxm в которой строки и столбцы соответствуют дугам (ребрам) графа. Элементы {0,1} 1 – дуга предшествует другой дуге;Для неориент 1 если ui и uj смежны.

Сеть -взвешенный конечный граф без цикла и петель ориентированный в одном направлении от истока (I) к стоку (S). Пропускная способность ребра – максимальное кол- во rij вещества, которое можно пропустить через ребро (i ,j) за ед. времени. Кол-во вещества Хij, проходящее за единицу времени по ребру (i ,j) – поток по ребру (i ,j). Будем считать, что поток по ребру (i ,j) равен Хij, тогда по ребру (j,i) равен – Хji , а Хii=0.

Если поток по ребру xij<rij его пропускной способности то ребро не насыщено, если равен, то ребро насыщено. Совокупность потоков Х={Хij}- поток по сети. Из физического смысла грузопотока следует, что поток по сети не может превышать его пропускной способности xij<=rij.(1) Для любой вершины кол-во вещества поступающего в данную вершину = кол-ву вещества вытекающего из неё (2)(кроме I,S) Условие сохранения потока: в промежуточных вершинах потоки не создаются и не исчезают, значит, общее кол-во вещества вытекающего из истока совпадает с общим кол-вом поступающего стоку, т.е. (3). Линейная функция f - мощность потока. Можно сформулировать задачу о максимальном потоке: Найти совокупность Х*={Хij*} потоков по всем ребрам сети, которые удовлетворяют условиям (1)-(3) и максимизирует линейную функцию f. задача ЛП. Заметим, что числа Хij образуют квадратную матрицу n-го порядка, на глав. диаг. 0 , а элементы симметричные относительно гл. диагонали равны по модулю, противоположны по знаку.

Разрез на сети: Пусть дана сеть, разобьем мн-во вершин на два непересекающихся подмн-ва A и B так чтобы , а тогда говорят, что на сети произведен разрез, отделяющий I от S. Появятся ребра, у которых начальные точки в A, а конечные в В. Совокупность таких ребер называется А/B разрезом на сети величина – пропускная способность разреза, величина – поток по разрезу.T: Если возможно построить поток, величина которого равна пропускной способности разреза, то этот поток будет максимальным. А разрез будет обладать минимальной пропускной способностью. Теорема Форда-Фалкерсона: На любой сети максимальная величина потока из I в S равна min rij разрезов отделяющих исток от стока. Алгоритм: Подмн-ву А отнесем все вершины достижимые из истока хотя бы по одному пути, состоящему из ненасыщенных ребер, а к В все остальные, т.е. которые нельзя достичь по ненасыщенным ребрам. Возможны два случая 1) 2) .Если 2, то построенное разбиение разрез. По условию разбиения для любой вершины из мн-ва А сущест. путь из I, состоящий из ненасыщенных ребер. А для любой вершины из мн-ва В такого пути нет, т.е. любое ребро разреза будет насыщенным Xij=rij просуммировав по i и j по теореме поток Х максимальный. Если 1, то существует путь из ненасыщенных ребер, ведущий из I в S. По ребрам этого пути можно пропустить дополнительный поток Потоки по остальным ребрам сети остаются прежними. Мощность суммарного потока возрастает на величину .Получим новый поток Х1={Хij1}.

Тогда имеем алгоритм: 1. Строим некоторый начальный поток Х0 2. Cоставим подмн-ва А вершин(достижимых из истока по ненасыщенным ребрам.) Если сток не попал, то поток максимальный. Если нет то 3. 3. Выделить путь из I в S, состоящий из ненасыщенных ребер и увеличить поток Хij по каждому ребру этого пути на величину .т.о, будет построен новый поток Х1 Далее п.2. На каждом шаге, по крайней мере, одно из ненасыщенных ребер становится насыщенным. Т.е. через конечное число шагов будет построен максимальный путь т.к. число ребер сети конечно.

2(1).Статистические игры. Критерии для принятия решений. C целью решения неблагопр. последствий в каждой конкр. ситуации следует учитывать степень риска и имеющуюся инфу. Лицо, принимающее решение вступает в игровые отнош. с некоторым абстракт. лицом, назовем его природой. Иногда лицо, принимающее решение располагает некоторыми вероятностными характеристиками состояния природы. Любая хозяйств. деятельность человека может рассматр. как игра с природой. В широком смысле природа – совокупность неопределенных факторов влияющих на эффективность принимаемых решений. Задача ЛП в этом случае – принятие наилучшего управленческого решения. Статистические игры представляют собой основную модель принятия решений в условиях частичной неопределенности. П – мн-во состояний природы, а мн-во решений игрока – А. Отдельное состояние природы Пj, а отдельн. состояние игрока Аi. Во взаимоотношениях с природой игрок отыскивает оптимальную стратегию Аi. При этом он может пользоваться как чистыми, так и смешанными стратегиями. (Стратегия - совокупность правил, однозначно определяющая последовательность действий игрока в конкрет. ситуации. Чистая стратегия игрока - возможный ход игрока, выбранный им с единичной вероятностью. Смешанная стратегия игрока – вектор р (р1,…рm), где означает вероятность принятия i-й чистой стратегии.) Получим матрицу[aij ]mxn – платежная матрица статистич. игры. Элемент aij – выигрыш игрока, если он использует стратег. Аi при состоянии природы Пj. Иногда при решении статистической игры используется матрица рисков. Элементы этой матрицы rij равны разности между максимально возможным выигрышем и тем выигрышем, который получит игрок, применяя стратегию Аi при Пj. Оптимальную стратегию игрока можно определить, используя ряд критериев: Критерий Байеса (используется при известном распределении вероятностей состояний природы qj) За оптимальную принимается та стратегия, при которой максимизируется средний выигрыш. В случае риска за оптимал. стратегию, принимается Аi при которой минимизируется риск Критерий недостаточного основания Лапласа: Все вероятности состояний природы полагают равновероятностными. q1=q2=…=1/n. Оптимал. стратегия, которая обеспечивает максимальн. средний выигрыш.Максимальный критерий Вальда: совпадает с выбором за оптимал. принимается чистая стратегия, кот в наихудших условиях гарантирует max выигрыш. Критерий минимального риска Сэвиджа: Оптимал. стратегия, при которой величина максимального риска минимизируется в наихудших условиях. Критерий Гурвица: За оптимал. принимают ту, для которой выполняется соотношение, в случае =0 имеем критерий крайнего оптимизма. =1 получим критерий пессимизма Вальда.

3(25).Применение интерполирования. Интерполирование – процесс построения интерполяционной ф-ии или процесс нахождения промежуточных значений табличной функции (способ приближения ф-ии). Пусть y=f(x), x[a,b], пусть задана система точек (x₀,y₀), (x₁,y₁), …, (x_n,y_n), кот. явл-ся приближением ф-ии в след. смысле: в заданных узлах x₀, …x_n ф-ция принимает значения y₀, …, y_n. Система этих узлов м.б. аппроксимирована нек. полиномом и P_n(x_i)=f(x_i). (x) =f(x)- - остат член. Простейшая задача И. состоит в том, чтобы построить полином знач. которого совпадают с знач. ф-ции в выбранной системе узлов. И полином Лагранжа: где (x)=(x-x₀)…(x-x_n). , Т: Если ф-ция f(x) на [ab] имеет непрерыв. производ. до (n+1) порядка включ, то остат член df по ф-ле: зависит от х. Л можно использовать при любом расположении узлов, но при прибавлении нового узла надо пересчитывать многочлен, т.к. его члены зависят от узлов интерполир. Н не обладает этим недостатком

Разностное отношение Пусть y=f(x_i)(знач ф-ции в т.х₀..х_n). Пусть -разность 1-го порядка…. - n-ого. f(x_k+1,x_k)=(f(x_k+1)-f(x_k))/(x_k+1-x_k) –разност. отнош. 1 пор-ка. f(x_k+1,x_k,x_k-1) = (f(x_k+1,x_k)- f(x_k,x_k-1))/(x_k+1-x_k-1) – 2 пор-ка. В численном анализе разностные отношения играют роль производных. Интерполяционный полином Ньютона: 1) интерпол вперед, неравностоячие узлы P_n(x)=f(x₀)+(x-x₀)f(x₀,x₁)+(x-x₀)(x-x₁)f(x₀,x₁,x₂)+…+(x-x₀)(x-x₁)…(x-x_n-1)f(x₀,x₁,…,x_n)). 2)равностоящ. узлы х_k=x₀+kh: . Полиномы Л. и Н. совпадают. Будем рассматривать полиномы для случая равноотстоящих узлов: x_i=x₀+ih, h=(x_n-x₀)/n Числ. Дифф. Некорректная задача (3 усл наруш).При числ. диф. f(x) замен. многочлен. P_n(x);и олагают что f’(x)P’_n(x). Рассм. полином Н f’(x)f(x₀,x₁)+(L₀+L₁)f(x₀,x₁,x₂)+(L₀L₁₊L₁L₂₊L₀L₂) f(x0,x1,x2,x3)+…;L_k=x-x_k. Для равностоящ.: , где t=(x-x₀)/n или x=x₀+th. . Найдем производную в узле интерполирования . Погрешность для этой формулы |R’|<=(hM_n+1)/(n+1),где M_n+1 –максимум n+1производной. Общая погрешность численного дифф. f’(x₀)=(f(x₀+h)-f(x₀))/h,  - точность с которой находим знач. ф-ции, тогда общая погр-сть: будет 2/h+M₂h/2=g(h).-точка минимума расчет с шагом меньшим оптимального приводит к ошибкам. Численное интегрирование. Необход. в числ. взятии интеграла диктуется след. причинами: И. не берется, подынтегральная ф-я задана таблично, получ. преобразов. имеют сложный аналитиче. вид. Пусть fC[a,b]. , A_k – квадратурные коэфф. x_k – квадратурные узлы, а процедура взятия интеграла наз. механ. квадратура. Идея: ф-я заменяется интерполяц. полиномом Равноотст. узлы t=(x-x₀)/h A_j не зависит от оузлов, завис. от [a,b]. 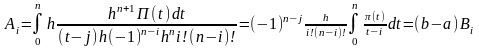B_i-зависит от n.: ф-ла Ньютона-Котеса. 1)n=1 формула трапеций.:B₀=1/2;B₁=1/2 2) n=2 метод парабол или метод Симпсона: B₀=1/6; B₁=2/3; B₂=1/6; метод парабол или метод Симпсона.

4(14).Решение СЛАУ уравнений прямыми и итерационными методами. Прямыми методами наз. методы, позволяющие получить реш-е сис(1) за конеч. число ариф. операций. метод Крамера, метод Гаусса, LU-метод и т.д.Достоинства заранее известно число итераций, что позволяет отслеживать результат процесса.(важно для работы динамич. Системы в реал времени- фвтопилот).Минусы: ошибка допуч. На шагах могут сильно изменить решение Итерационные методы (методы послед-х приближений): реш-е сис(1) нах-ся как предел последовательных приближений при , где n номер итерации. При использовании методов итерации обычно задается некот малое число 0 и вычисления проводятся до тех пор, пока не будет выпол-на оценка . К этим методам относ метод Зейделя, метод простой итерац и т.д.Недостаток: не знаем когда закончится(в реал времени использ. нельзя)Достоинства: самоисправляющиеся. Если итерац. Процесс сходится, то ошика допущенная на шаге трактуется как нов. начальн. приближ. И не сказывается на окончат. решении. Можно работать с большими матрицами. Метод Гаусса Пусть требуется решить систему уравнений Ax=B(1). Метода Гаусса состоит в том, что система сводится к A’x=b’(2), где A’ – треугольная из последнего уравнения (2) находят x_n, из предпоследнего x_n-1 и т.д. Переход от (1) к (2) наз. прямым ходом метода Гаусса, нахождение x_n, x_n-1 и т.д. – обратный ход. Метод Гаусса относится к точным методам. Метод Гаусса с выбором главного элемента. Суть: сначала выбирают уравнение, содержащее наибольший по модулю коэфф. (главный элемент), затем делят это уравнение на главный элемент и из остальных уравнений системы исключают неизвестное, определяемое этим элементом. Для удобства этот элемент можно поместить в первую строку и первый столбец. Затем, оставляя неизменным ур-е с главным элементом, делим на этот главный элемент и из остальных уравнений исключаем неизвестное, определяемое этим главным элементом и т.д. Получается матрица диагонального вида. При применении этого метода переставляются уравнения, что приводит к изменению порядка исключения неизвестных и во многих случаях это приводит к уменьшению погрешности связанной с округлениями при вычислениях. М-д прост итерации Покажем как прим. принцип сжатых отображений к исследованию сх-ти итерац. метода. Пусть система ур-й приведена к виду x=Bx+b (1). Правую часть этого ур-я обозначим через Ф(х)=Вх+b. Где Ф можна рассматривать как отображение Ф:RⁿRⁿ. Решение (1) сводится к отысканию неподвижной точки отображения Ф т.е. Ф(х)=х. Для того чтобы Ф имело единств. неподв. точку надо чтобы Ф было сжатием. Итак, если Ф – сжатие, то оно имеет в пространстве Rⁿ единственную неподвижную точку x^* и к ней сходится итерационный процесс x⁽ⁿ⁺¹⁾=Ф(x⁽ⁿ⁾), где х⁰R. (3) При каких условиях Ф будет сжатием? Ответ зависит не только от Ф, но и от выбора метрики в Rⁿ. Рассмотрим часто встречающиеся метрики: Кубическ.. ₁(x,x’)=max|x_i-x_i’| Рассмотр. Расстояние между векторами Ф – сжатие если 2. Октаэдрическая метрика сжатие если 3. Сферическая метрика сжатие если . Если выполняется одно из трех условий, то Ф – сжатие и по принципу Банаха для его в Rⁿ существует единств. неподвиж. точка x^* к которой сходится итерац. процесс.Т.е док. Т: Если для матрица B сис-мы (1) выполняется одно из усл. То система СЛАУ имеет ед. реш., которое можно получить по ф-ле (3). Скорость метода df след. соотнош.: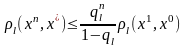 , Если имеем: Ax=b -> Ax-b=0 -> -t(Ax-b)=0 -> x- t(Ax-b)=x -> x=(E-tA)x+tb. ИП: xⁿ⁺¹=(E-tA)xⁿ+tb. Для сходимости надо: ||E-tA||<1. В этом процесс до конца просчетов должны оставаться значения n+1 шагов. От этого недостатка избавлен метод Зейделя(явл. модификац. м-да. простой итераций): М-д позволяет сразу использовать при вычисл. послед. координат вектор xⁿ⁺¹. Усл. Сходимости одинаковые. Скорост быстрее.Останов Принцип сжат отображ: Пусть R- полное метрич про-во и f-отображ f:R->R явл. Сжатием, тогда оно имеет в R единств. Неподвиж. Точку к которой сходится последовательность приближ решений получ. по ф-ле x_n+1=f(x_n). Полное м.пр. – пр-во вкотором всякая фундаментал. пос-ть сх-ся.

5(17).Решение одномерных нелинейных уравнений сверхлинейными методами.

Принцип сжат отображ: Пусть R- полное метрич про-во и f-отображ f:R->R явл. Сжатием, тогда оно имеет в R единств. Неподвиж. Точку к которой сходится последовательность приближ решений получ. по ф-ле x_n+1=f(x_n). Полное м.пр. – пр-во вкотором всякая фундаментал. пос-ть сходится. Область сходимости – совокупность нач. приближ, при которых м-д сходится. Решаем ур-ие F(x)=0. Приведем x=f(x). Где f(x)=x- F(x). Пусть на [a,b] ф-ция 2-ды диффер. и производные не равны 0. Ф-ция монотонна. F(a)F(b)<0 -> сущест. единственный корень Метод Ньютона.(касательных). Запишем уравнение в виед x=x- F(x), где -непрерывна в х^*. В качестве =1/F’(x), то - метод Ньютона. Для док-ва сходимости данного метода применим принцип Банаха. Д-м, что отображение f – сжатие, где f(x)=x-F(x)/F’(x),

Подставим x=x*, f’(x*)=0, т.к. x* - корень F(x)=0. f(x)-непрерывна на отрезке. и f’ –непрерывна -> сущ-ет окр-сть корня, в кот. |f’(x)|<=q<1. Если выбрать x₀ из этой окр-сти, т.е. F(x₀)F’(x₀)>0, то отобр. f(x) явл-ся сжатием и по принципу Банаха метод будет сх-ся, т.е.xn->x* при n-> . Получим скорость сх-сти. Для этого разложим ф-цию F(x) в ряд Тейлора в окрестности т. xn: F(x)=F(x_n)+F’(x_n)(x-x_n)+F’’( )(x-x_n)2/2!, (x,x_n) Т.к. x* - корень ур-ия F(x*)=0, то 0=F(xn)+F’(xn)(x^*-xn)+F’’( )(x^*-xn)2/2!. Т.к. F’(xn) , то .Получим. Обозн. m1=min|F’(x)| для x [a,b], M2=max|F’’(x)| x [a,b].То . Из этой формулы видно, что метод Ньютона сходится с квадратичной скоростью.

Метод хорд и метод секущих Скорость сход –ти -линейная. Достоинства: 1.Широкая область сходимости 2.Легко программировать. Недостатки: медленная скорость сходимости. Если , то - метод секущих. Для метода секущих сверхлинейная скорость сх-сти равна Метод простой итерации, обладает линейной скоростью сходимости, метод секущих и метод Ньютона – сверхлинейной. Теорема: Пусть в области D сущ. решение уравнения F(x)=0(1), F 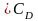, сущ. огранич. обратный оператор и если х₀ и начальная шагавая длина , таковы что тогда итерационный процесс (2)-(4) со сверхлинейной скоростью сх-ся к решению уравнения (1) , , - метод Пузынина

6(13).Основные понятия БД. СУБД. База данных – это сов-ть данных и их интерпретации. Предметная область – часть реального мира, отраженная в базе данных. СУБД взаимодействует с БД, приним. запросы от инициатора, обрабатывает их, предоставл. рез-ты выполн. запроса. Виды БД: ерархические – могут хранить только древовидные структуры; сетевые – отличаются от иерархических тем, что запись может входить в более чем 1 групповое отношение; реляционные –В реляционных БД вся информация хранится в виде таблиц. Каждая строка таблицы представляет собой запись, а столбец поле. Сущность – любой различимый объект, информация о котором храниться в базе данных.Атрибут – поименованное свойство сущности, значение которого фиксируется в базе данных.Ключ –мин. Набор атрибутов, которые однозначно df экземпляр сущгости. Связь - ассоциативные отношения между сущностями. Степень связи – число сущностей, которые ассоциатированные с одним экземпляров сущности. Координальность – возмодность наличия связи со стороны экземпляра сущности(есть/нету). Сущесив. 3 этапа проектиров. БД. 1.Инфологичекая модель данных - обобщенное описание предметной области, не зависящее от конкретной СУБД. В инфо. Моделиров. выделяют два уровня: концептуальный и логический. На концептуальном уровне по описанию предметной области строится общая модель данных, которая представляет собой схему с описанием всех элементов данных и отношений между ними. На логическом уровне вып. детализация и уточнение эл-ов концептуальной схемы: описание характеристик элементов (атрибутов) и связей между ними. Одним из наиболее удобных инструментов унифицированного представления данных, нез-ого от реализующего его программного обеспечения, явл. модель "сущность-связь" (ER). Сначала выделяются независимые(сущность для которой св-ва ее экземпляров не завис. От cв-в ассоциир. сущностей(отображ прямоугольником)) и зависимые сущности. Среди сущностей выделяют: ассоциацию-сущность экземпляра кот., имеет связь с экземпляр. Др. сущности один ко многим.(ромб) Характеристика – завис сущ, связь один к одному», «один ко многим» .(трапеция) Обозначение – зав сущ, один к одному», «один ко многим и нет явной зависимости(параллерограм). 2. Даталогическая преобразов элементов логич модели в конкрет таблицы. Важным преобразов здесь явл нормализация таблиц.3. Физическая –данные представл в виде файлов на физ носителях. Др.возможным вариантом проектирования БД явл. сбор инф-ции об объектах предметной области в одной или нескольких таблицах. Любое представление данных может быть вып. в виде двумерных таблиц – отношений (relation). Элемент данных в реляционной модели – это отдельное атомарное (неразложимое) для данной модели значение данных. Др. базовыми понятиями реляционной модели данных явл.: Домен – это множество атомарных значений одного и того же типа.(представл столбцами таблицы D1). Отношение на доменах сост. из заголовка и тела. Заголовок отношения – это фиксиро.множество атрибутов A1, A2, …, An, для которого существует взаимно-однозначное соответствие между Ai и определяемыми ими доменами Di (i=1,…,n). Кортеж – это множества пар атрибут-значение (Ai:Vi), (i=1,2,...,n). Тело отношения состоит из меняющегося во времени множества кортежей. Степень отношения – это число его атрибутов. Множество атрибутов отношения назыв ключом если удовлетвор усл: уникальность(ни один из кортежей не имеет одинаковое значение), минимальность(нельзя удалить атрибут чтоб не нарушилось cв-во 1).Важной задачей явл –нормализация таблиц. . Под нормализацией будем понимать декомпозицию исходной таблицы на две или больше взаимосвязанных таблиц в соответствии с определенными правилами. Результатом декомпозиции является нормальная форма, под которой понимается некоторое требование к таблице. Различают пять упорядоченных нормальных форм. Основная цель нормализации – удобство выполнения трех основных операций редактирования таблицы – вставка, удаление, изменение строк. Любая декомпозиция исходной таблицы должна быть обратима. Другими словами, процесс обратный нормализации должен привести к исходному отношению.1нф – на пересеч каждога столбца и строки стоит атомарное значение и ключ поля не пусты. 2нф – 1нф и любая функциональная зависимость столбцов таблицы, не входящ в первич ключ, функционально полно зависит от первичного ключа.(Функц. Зависимость – если для каждого значения атрибута B соответствует одно знач атрибута А. Функц. Полная завис – атрибут А функц зависит от B но не зависит ни от какой части атрибута В) 3нф-2нф икаждый атрибут нетранзитивно зависит от первичный ключа(функц завис атрибута С от атрибута А через атрибут В – транзитив зависимость) нф Бойса-Кодда- 2нф и каждая возможная функц зависимость между ее атрибутами явл полной функц зависимостью от возможного ключа. 4нф – 3нф и при наличии многозначной зависимости вида А->>В , зависимость всех остальных атрибутов от А явл функц. На практике нф выше 3 встречаются оч редко.

7(14).Глобальная компьютерная сеть интернет. Принципы функционирования. Основные услуги и сервисы, методика использования. В 60-е годы, после фирма Rand Corporation, один из мозговых центров США, впервые предложила создать децентрализованную компьютерную сеть, покрывающую всю страну. Основной идеей проекта была децентрализация управления и подчинения, чтобы выход из строя одного или нескольких сегментов сети не привел к ее разрушению. Такая структура м. б. осуществлена только при наличии между узлами сети множественных связей. К осени 1969 года появилася сеть ARPANET, состоявшая к тому времени из четырех узлов. Ученые получили возможность передавать данные и совместно пользоваться удаленным доступом к компьютерам, а в 1973 году к сети впервые были подключены и зарубежные узлы. Сеть из этих 5 центров обычно называется "магистральным хребтом Internet в США". Однако, без сомнения, причиной наиболее серьезного развития Internet в 90-х годах стало создание World Wide Web. В ноябре 1990 года Тим Бернс-Ли создал первый прототип WWW-сервера. WWW как активно функционирующая система не выходила в свет до 1992 года. В последующие годы развитие Internet и WWW происходило еще более быстрыми темпами.

Стек протоколов TCP/IP — набор сетевых протоколов разных уровней модели сетевого взаимодействия , используемых в сетях. В стеке 4 уровня: сетевого интерфейса(передача битов по каналам связи), межсетевой(передача данных через составную сеть без установления соединения по наиболее рациональному маршруту.Использует Ip протокол) , транспортный(передача пакетов за счет образование логического соединения, UDP,TCP протоколы), прикладной(набор протокол с помощью которых пользовательполучает доступ к ресурсам сети). В стеке Tcp/Ip три типа адресов: локальные(или MAC адрес – назначается сетевым оборудованием и явл уникальным, состоит из 6 байт 11-СС-12-3С-2С-22), ip-адреса(основ тип адресов на котором сетевой уровень передает пакеты между сетями, 4 байта – 109.23.12.100. Назначаются админом сети во время конфигурирования оборудования. Состоят из двух частей: номер сети и номер узла. Номера сети назнач централизованно(если internet) и произвольно(если работает локально). Номер узлов - админ назначает произвольно из разрешенного диапазона) .символьные доменные (строятся по иерархическому признаку. Составляющии имени разделены точкой и перечисл в след порядке: простое имя узла. имя группы. Более крупной группы…до домена высокого уровня. Ru, by. Base.sale.ru). DNS-система доменных имен –централизованная служба, основанная на распределенной базе отображений доменной имя - ip-адрес. Dns- сервер поддерживает распределенную базу отображений, а dns- клиенты обращаются к серверам с запросом о разрешении доменного имени в ip-адрес. Для того, чтобы можно было безошибочно получать нужную информацию и в нужном формате используется строка символов, которую называют универсальный указатель ресурса или URL. Эта строка однозначно идентифицирует любой ресурс в сети Internet. Именно такая строка отображается в поле «Адрес» обозревателя Internet Explorer, когда мы «гуляем» по Internet (Протокол:// Доменное имя/ Путь/ Имя файла). Протокол – это набор правил (http:// – протокол передачи гипертекста) Путь, состоящий из имен папок, разделенных символом / (слэш), последовательно открывая которые можно «добраться» до нужной информации. Имя файла, который содержит нужную информацию.

Всемирная паутина — WWW — это средство поддержки системы гипертекста на Internet. WWW напоминает паутину, в которой каждый узел или WWW-страница представляют собой систему расходящихся связей с другими узлами или WWW-страницами, каждая из которых, в свою очередь, связана с еще большим числом страниц. Гипертекст — это обыкновенный текст, содержащий ссылки, которые ассоциированы с определенными ключевыми словами и фразами и которые содержат дополнительную информацию об этих ключевых словах и фразах. Ф-ия ссылок — связывать одну страничку (или файл) с другой. Для обзора информации, полученной от веб-сервера, на клиентском компьютере применяется специальная программа — веб-браузер. Основная функция веб-браузера — отображение гипертекста. В настоящее время наметились две тенденции в развитии Всемирной паутины: семантическая паутина и социальная паутина. Семантическая паутина предполагает улучшение связности информации во Всемирной паутине через введение новых форматов метаданных. Социальная паутина полагается на работу по упорядочиванию имеющейся в Паутине информации, выполняемую самими пользователями Паутины. Существует также популярное понятие Web 2.0, обобщающее сразу несколько направлений развития Всемирной паутины.

FTP, сокращение от file transfer protocol, протокол передачи файлов — это Internet-протокол, позволяющий получать и передавать текстовые и двоичные файлы между 2-мя компами., связанными между собой локально или глобально. При этом комп. Платформы могут быть различны. FTP чаще всего используется для получения файлов из архивных хранилищ файлов. За прошедшие несколько лет в Internet появилось огромное количество FTP-узлов — "складов" ПО, утилит общего назначения и различ­ных файлов поддержки. Узлы FTP, предназначенные для поддержки покупателей аппаратных и программных средств, обычно широко рекламируются. Поэтому пользователи, заинтересованные в информации, хранящейся на этих узлах, могут с легкостью отыскать их в Internet и разобраться в их содержимом, К сожалению, многие иные узлы FTP не подпадают под эту категорию и в большинстве своем остаются неизвестными, кроме тех случаев, когда информация о них передается от пользователя к пользователю или включается в списки FTP-узлов в книгах, подобных этой.

E-mail — сокращенное обозначение электронной почты. Это простая с-ма, созданная для получения и посылки сообщений по сети. Электронная почта — это еще одна служба Internet, традиционно существовавшая вне WWW, доступ к которой теперь по умолчанию включается в последние версии браузеров. Эл. Почта воплощение структуры клиент-сервер. Так доставка осуществ спец хостами, делается автоматически. E-mail подразумевает адресацию своих пользователей. Вид адреса пользователя: someuser@some.domoin. Можно разбить на две части: с конца до @- имя домена. В каждом письме сущ поля содержащие df инфу: Адрес получ, заголовок, текст, те кому отправл копии письма. Обязат поле – адрес получателя. Для написание письма используют почтовые клиенты –Outlook The bat. Сушеств несколько возможностей адресации: множественная рассылка(более чем 1-му одресату), множеств рассылка без указания адресата –получ не знают кому еще были посланы копии. Адресная книга –список людей, которым посылаются обычно. Маршрутизация – использ маршрутиз, вы посылаете почу списку адресатов так, что она будет последовательно передаваться от одного к другому.

8(24).Равномерное распределение случайной величины. Часто приходится сталкиваться с действительными величинами значения, которых зависит от случая. Случайной наз.величина кот.в результате испытаний из множ-ва своих возможных знач.принимает единственное знач,зависящае от случайных причин учесть кот.невозможно. Случ.величина(СВ) – числовая функция,определенная на простр-ве элементарных событий ξ=ξ(ω) ,ω Ω.Cуществует два типа СВ – дискретные(принимает конечное или бесконечное счетное мн-во знач.) и непрерывные(СВ возможные знач.кот.непрерывно заполняют некот.интервал числовой оси). Фун-ей распределения СВ наз. вероятность того,что СВ принимает знач.< чем х,т.е.F(x)=P(X<x) для любого xєR Св-ва функции распределения: 1) 0≤F(x)≤1 по определ. Вероятности; 2) P(a≤X<b)=F(b)-F(a),где a,b=const,а,bєR. ДОК.Введем события A={x<a}; B={a≤x<b}; C={x≥b}. А+В+С=Ω; P(А+В+С)=P(Ω)=1

Т.к.события АВС попарно несовмесны,то P(А+В+С)=P(A)+P(B)+P(C);Р(В)=1-Р(С)-Р(А)=P( )-P(A)= =P{x<b}-P{x<a}=F(b)-F(a)…3) x1≤x2=>F(x1)≤F(x2), x1,x2єR…4) lim x→-∞F(x)=0 и lim x→+∞F(x)=1

Производная от функции распределения непр.СВ – плотность распределения непрерывной СВ,т.е.f(x)=F’(x)

Св-ва плотности распределения: 1) f(x)≥0, ;2) - условие нормировки непрерывной СВ.Д-во .

СВ имеет равномерное распределение на [a,b] если плотность её распределения имеет вид. Рассм.ф-ю распр.СВ,им.равномерное распределение .Для х≤a , для a<x<b , если x>b .Следоват.

Найдем математическое ожидание

Дисперсия СВ

(Мат. ожидание приблизительно равно среднему арифметическому наблюдаемых значений, и тем точнее, чем больше испытаний. Дисперсия – мат. ожидание квадрата отклонения СВ. от её мат. ожидания, характеризует меру разбросанности значений СВ. около мат. ожидания. )С равномерным распределением сталкиваются, когда по условию опыта СВ. принимает значения из [a,b] и все значения, полученные из промежутка возможны в одинаковой степени.