5.6 Середня гармонічна, особливості її використання та обчислення

Середня гармонійна звичайно застосовується у випадках, коли усереднюванню підлягають не самі варіанти, а зворотні їм числа або коли є дані про загальний обсяг явища й індивідуальні значення ознаки, але немає відомостей про кількість одиниць даного явища (частотах).

НАПРИКЛАД: є зведення про врожайність і валовий збір зерна, але немає даних про площу зернових (або є відомості про виручку і ціну одиниці товару, але немає кількості реалізованих товарів). Проста середня гармонійна (незважена) визначається:

1 Знаходять середню арифметичну зі зворотних величин:

2

.

3 Величина, зворотна отриманій середній арифметичній і буде середньою гармонійною:

4

.

Слід зазначити, що в теорії статистики немає більш заплутаного і по-різному трактованого питання, ніж питання про середню гармонійну.

Багато авторів вважають, що це не самостійний вид середньої, а спосіб скороченого підрахунку середньої арифметичної. Разом з тим у всіх відомих підручниках середня гармонійна розглядається як різновид середньої і на це треба зважати.

Отже, середня гармонійна зважена є не що інше як перетворена середня арифметична.

Формула для її розрахунку має такий вигляд:

, де .

У багатьох підручниках кочує стандартний приклад розрахунку середньою гармонійної зваженої:

• є середня врожайність зернових по господарствах району і валовий збір зерна , тобто 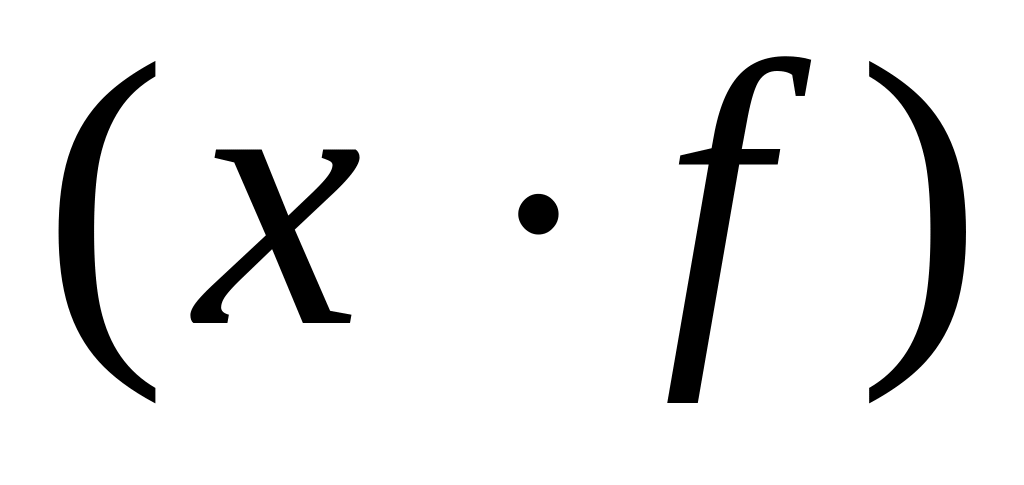, але немає відомостей про площу під зернові, тобто немає частот.

В цьому випадку пропонується обчислювати середню врожайність по району за допомогою середньої гармонійної зваженої.

ПРИКЛАД: Нехай є 3 господарства, які висіяли цукрові буряки.

Господарства	Урожайність, ц/га	Валовий збір, ц
I II III	260 210 230	2800 3400 2600
Всього		8800

Валовий збір

ц/га

5.7 Середня геометрична та квадратична, умови їх застосування та способи обчислення

Природу і сутність середньої геометричної краще всього можна пояснити на такому простому прикладі:

ПРИКЛАД: Нехай є два числа: 4 і 16. Середня арифметична з них дорівнює 10. Число 10 на стільки ж більше 4, на скільки воно менше 16: 4 < 10 < 16.

Нам потрібно знайти число, яке буде в стільки ж разів більше 4, в скільки разів воно буде менше 16. Таке число можна знайти за формулою загального члена геометричної пропорції

. Воно і є середньою геометричною для чисел 4 і 16.

Таким чином, якщо середня геометрична обчислюється з ряду величин (з незгрупованих даних), то вона дорівнює кореню n степені з добутку цих величин.

Тобто ,

де – добуток .

Для підрахунку середньої геометричної необхідно значення Х прологарифмувати, тобто

.

У логарифмованому вигляді формула середньої геометричної нагадує формулу, середньої арифметичної з тією лише різницею, що замість натуральних величин фігурують їх логарифми.

Загалом же середня геометрична відрізняється від середньої арифметичної порядком дій над величинами:

• замість підсумовування величин знаходиться їх добуток;

• замість ділення обчислюється корінь відповідної степені.

Якщо середня геометрична обчислюється для варіаційного ряду, то тоді сума частот є показником степені кореня, а частота кожного з варіантів – показником степені варіанта.

ПРИКЛАД:

Варіанти (х)	Частоти (f)
4	2
8	3
10	1
11	2
Разом:	8

.

.

.

Середня геометрична знаходить в статистиці дуже обмежене вживання.

Вона використовується, в основному, при обчисленні середніх темпів зростання якого-небудь показника (продукції, населення і т.д.).

Середня квадратична застосовується у випадках, коли усереднюванню (узагальненню) підлягають величини, виражені у вигляді квадратних функцій.

НАПРИКЛАД, середні діаметри труб, коліс, стовбурів дерев і т.д.

Проста середня квадратична визначається за формулою

.

Зважена .

Якщо розраховувати різні види середніх величин на основі однієї і тієї ж первинної інформації, то отримаємо різні значення середніх, що обумовлено правилом їх мажоритарності:

.