Тема 2. Графический метод решения задач линейного программирования.

2.1 Геометрическая интерпретация задачи лп.

Графический метод основан на геометрической интерпретации задачи линейного программирования. Он применяется для решения задачи ЛП с двумя переменными, заданными в неканонической форме, и многими переменными, заданными в канонической форме при условии, что они содержат не более двух свободных переменных.

Рассмотрим задачу ЛП с двумя переменными

С геометрической точки зрения при решении задачи ЛП ищется такая угловая точка или набор точек из области допустимых решений (ОДР), на которой достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста целевой функции.

Для нахождения экстремального значения целевой функции при графическом решении задачи ЛП используют вектор на плоскости X₁OX₂, который обозначим Этот вектор показывает направление наискорейшего изменения целевой функции, он равен

где и - единичные векторы по осям OX₁ и OX₂.

Координатами вектора являются коэффициенты целевой функции .

2.2 Алгоритм решения задачи лп графическим методом.

Алгоритм решения задачи ЛП графическим методом состоит из следующих этапов:

1. Найти ОДР системы ограничений.

2. Построить вектор

3. Провести некоторую линию уровня функции , которая перпендикулярна

4. Перемещать линию уровня по направлению вектора , если задача ЛП решается на максимум, и в направлении, противоположном , если задача ЛП решается на минимум. Перемещать линию до тех пор, пока у неё не окажется только одна общая точка с ОДР. Эта точка определяет единственное решение задачи ЛП и является точкой экстремума.

Если линия уровня совпадает с одной из сторон ОДР, то задача ЛП будет иметь бесконечное множество решений.

Если ОДР представляет собой неограниченную область, то целевая функция может быть неограниченна.

Задача ЛП может быть неразрешима, когда определяющие её ограничения окажутся противоречивыми.

5. Найти координаты точки экстремума – точки оптимума – и значение целевой функции в найденной точке.

2.3 Примеры решения задачи лп графическим методом.

Рассмотрим несколько примеров.

Пример 1. Максимизировать линейную форму F = x₁+ x₂ при ограничениях:

Построим прямые

1. x1	0	-2
   x2	3	0

   3x₁ – 2x₂ = – 6

2. 3x₁ + x₂ = 3

x1	0	1
x2	3	0

3. x₁ = 2

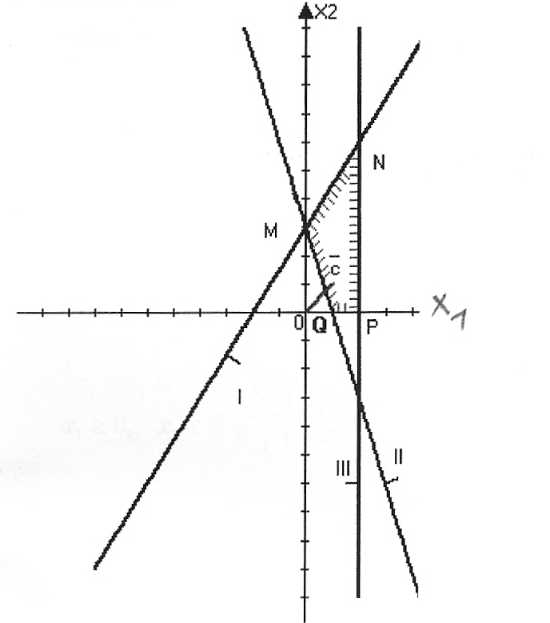
Учитывая знаки неравенств, определим полуплоскости решений и, таким образом, область допустимых решений системы – _{четырехугольник MNPQ}.

Построим 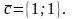Тогда линия уровня при выходе из четырехугольника решений пройдёт через точку N. Координаты точки N найдём как пересечение двух прямых I и III:

Тогда линейная функция F принимает наибольшее значение в точке N, т.е. максимизируется

Пример 2. Минимизировать функцию F = x₁+ x₂ при ограничениях:

Построим прямые

1. x1	0	3
   x2	3	0

   x₁ + x₂ = 3

2. x₁ + x₂ = 7

x1	0	7
x2	7	0

3. x₂ = 1

4. x₂ = 4

5. x₁ = 4

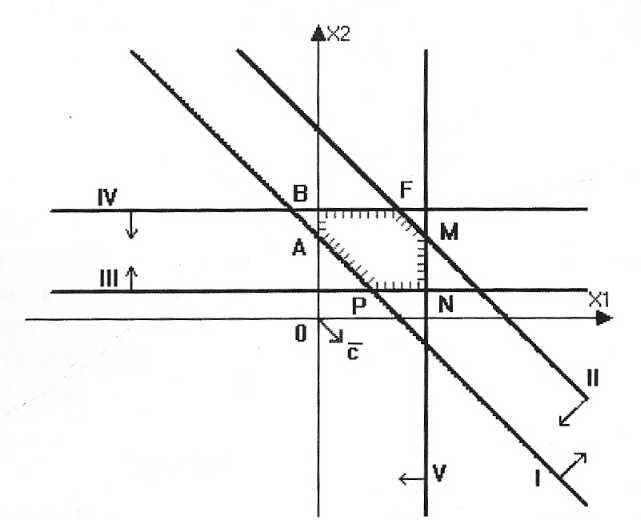
Область допустимого решения системы – многоугольник ABFMNP. Вектор Линия уровня, выходя из многоугольника решений в направлении, противоположном , пройдёт через точку B(0;4). Тогда

Пример 3.

Полуплоскости, определяемые системой неравенств, не имеют общих точек. ОДР – пустое множество.

Таким образом, по причине несовместимости условий задачи, эта задача решения не имеет.