- •Глава 1. Введение в автоматизированное проектирование
- •1.1. Понятие проектирования
- •1.2. Принципы системного подхода
- •1.3. Уровни проектирования
- •1.4. Стадии проектирования
- •1.5. Модели и их параметры в сапр
- •1.6. Проектные процедуры
- •1.7. Жизненный цикл изделий
- •1.8. Структура сапр
- •1.9. Введение в cals-технологии
- •1.10. Этапы проектирования автоматизированных систем
- •Лекция 2. Техническое обеспечение сапр
- •2.1. Требования к техническому обеспечению сапр
- •2.2. Вычислительные системы для сапр
- •2.2.1. Процессоры эвм
- •2.2.2. Память эвм
- •2.2.3. Мониторы
- •2.2.4. Периферийные устройства
- •2.2.5. Шины компьютера
- •2.3. Типы вычислительных машин и систем
- •2.4. Персональный компьютер
- •2.5. Рабочие станции
- •2.6. Архитектуры серверов и суперкомпьютеров
- •2. В.Н. Дацюк, а.А. Букатов, а.И. Жегуло/ методическое пособие по курсу "Многопроцессорные системы и параллельное программирование". -http://rsusu1.Rnd.Runnet.Ru/tutor/method/m1/content.Html
- •2.7. Примеры серверов
- •2.8. Суперкомпьютеры XXI века
- •Лекция 3. Математическое обеспечение анализа проектных решений
- •3.1. Требования к математическим моделям и методам в сапр
- •3.2. Фазовые переменные, компонентные и топологические уравнения
- •3.3. Основные понятия теории графов
- •3.4. Представление топологических уравнений
- •3.5. Особенности эквивалентных схем механических объектов
- •3.6. Методы формирования математических моделей на макроуровне
- •3.7. Выбор методов анализа во временной области
- •3.8. Алгоритм численного интегрирования систем дифференциальных уравнений
- •3.9. Методы решения систем нелинейных алгебраических уравнений
- •3.10. Методы решения систем линейных алгебраических уравнений
- •1. Alglib User Guide. - http://alglib.Sources.Ru/linequations/general/lu.Php. - Проверено 15.12.2009. Лекция 4. Математическое обеспечение анализа проектных решений
- •4.1. Математические модели для анализа на микроуровне
- •4.2. Методы анализа на микроуровне
- •4.3. Метод конечных элементов для анализа механической прочности
- •4.4. Моделирование аналоговых устройств на функциональном уровне
- •4.5. Математические модели дискретных устройств
- •4.6. Методы логического моделирования
- •4.7. Системы массового обслуживания
- •4.8. Аналитические модели смо
- •4.9. Уравнения Колмогорова
- •4.10. Пример аналитической модели
- •4.11. Модель многоканальной смо с отказами
- •4.12. Принципы имитационного моделирования
- •4.13. Событийный метод моделирования
- •4.14. Краткое описание языка gpss
- •1. Томашевский в., Жданова е. Имитационное моделирование в среде gpss. — м.: Бестселлер, 2003.
- •4.15. Сети Петри
- •1. В.Э.Малышкин. Основы параллельных вычислений. -2003 цит сгга, http://www.Ssga.Ru/metodich/paral1/contents.Html
- •4.16. Анализ сетей Петри
- •1. В.Э.Малышкин. Основы параллельных вычислений. -2003 цит сгга, http://www.Ssga.Ru/metodich/paral1/contents.Html Лекция 5. Геометрическое моделирование и машинная графика
- •5.1. Типы геометрических моделей
- •5.2. Методы и алгоритмы компьютерной графики
- •5.3. Программы компьютерной графики
- •5.4. Построение геометрических моделей
- •5.5. Поверхностные модели
- •1. Семенов а.Б. Программирование графических процессоров с использованием Direct3d и hlsl. -http://www.Intuit.Ru/department/graphics/direct3dhlsl/6/1.Html
- •5.7. Графический процессор
- •1. Пахомов с. Революция в мире графических процессоров // КомпьютерПресс, № 12, 2006.
- •5.8. Шейдеры
- •5.9. Геометрические шейдеры
- •5.10. Унифицированный графический процессор
- •1. Пахомов с. Революция в мире графических процессоров // КомпьютерПресс, № 12, 2006.
- •5.11. Примеры графических процессоров
- •Лекция 6. Математическое обеспечение синтеза проектных решений
- •6.1. Критерии оптимальности
- •6.2. Задачи оптимизации с учетом допусков
- •6.3. Классификация методов математического программирования
- •6.4. Методы одномерной оптимизации
- •6.5. Методы безусловной оптимизации
- •6.6. Подходы к решению задач структурного синтеза
- •6.7. Морфологические таблицы
- •6.8. Альтернативные графы
- •Лекция 7.
- •7.1. Интеллектуальные системы
- •7.2. Планирование процессов и распределение ресурсов
- •7.3. Методы локальной оптимизации и поиска с запретами
- •7.4. Методы распространения ограничений
- •7.5. Эволюционные методы
- •7.6. Простой генетический алгоритм
- •7.7. Кроссовер
- •7.8. Метод комбинирования эвристик
- •1. Норенков и.П. Эвристики и их комбинации в генетических методах дискретной оптимизации// Информационные технологии, 1999, № 1.
- •7.9. Примеры применения генетических методов
- •Лекция 8. Автоматизированные системы в промышленности
- •8.1. Системы erp
- •8.2. Стандарт mrp II
- •8.3. Логистические системы
- •8.4. Системы scm
- •8.6. Производственная исполнительная система mes
- •8.7. Автоматизированное управление технологическими процессами
- •8.8. Программирование для станков с чпу
- •8.9. Системы scada
- •8.10. Типовой маршрут проектирования в mcad
- •8.11. Типы сапр в области машиностроения
- •8.12. Основные функции cad-систем
- •8.13. Основные функции cae-систем
- •8.14. Основные функции cam-систем
- •8.15. Графическое ядро
- •Лекция 9.
- •9.1. Структура cad/cam систем
- •9.2. Машиностроительные сапр верхнего уровня
- •9.3. Маршруты проектирования сбис
- •9.4. Схемотехническое проектирование
- •9.5. Модели логических схем цифровой рэа.
- •9.6. Конструкторское проектирование сбис
- •9.7. Проектирование печатных плат
- •9.8. Назначение языка vhdl
- •Лекция10. Методическое и программное обеспечение автоматизированных систем
- •10.1. Типы case-систем
- •10.2. Спецификации проектов программных систем
- •10.3. Методика idef0
- •10.4. Методика idef3
- •10.5. Методика idef1x
- •10.7. Методика проектирования информационных систем на основе uml
- •10.8. Программное обеспечение case-систем
- •10.9. Интегрированные среды разработки приложений
- •Лекция 11. Технологии информационной поддержки этапов жизненного цикла изделий
- •11.1. Обзор cals-стандартов
- •11.2. Структура стандартов step
- •11.4. Интегрированная логистическая поддержка
- •11.5. Интерактивные электронные технические руководства
- •11.6. Стандарт aecma s1000d
- •11.7. Электронная цифровая подпись
- •11.8. Стандарты управления качеством промышленной продукции
- •Лекция 12. Технологии информационной поддержки этапов жизненного цикла изделий
- •12.1. Программное обеспечение cals-технологий
- •12.2. Язык html
- •12.3. Язык xml
- •12.5. Форматирование Web-страниц
- •12.6. Доступ к xml-документам
- •12.7. Мультиагентные системы
- •12.8. Технология soap
- •12.9. Компонентно-ориентированные технологии
5.2. Методы и алгоритмы компьютерной графики
К методам компьютерной графики относят методы преобразования графических объектов, представления (развертки) линий в растровой форме, выделения окна, удаления скрытых линий, проецирования, закраски изображений.
Преобразование графических объектов выполняется с помощью операций переноса, масштабирования, поворота.
Перенос точки из
положения
в
новое положение
![]() можно
выполнять по формулам типа
можно
выполнять по формулам типа
![]()
где
![]() —
приращение по координате
.
Однако удобнее операции преобразования
представлять в единой матричной форме
—
приращение по координате
.
Однако удобнее операции преобразования
представлять в единой матричной форме
![]() (1)
(1)
где
—
преобразующая матрица. При этом точки
и
в
двумерном случае изображают
векторами-строками 1×3, в которых кроме
значений двух координат, называемых
при таком представлении однородными,
дополнительно указывают масштабный
множитель
![]() .
Тогда перенос для случая 2D можно выразить
в виде (1), где
есть
табл. 1, а
.
Тогда перенос для случая 2D можно выразить
в виде (1), где
есть
табл. 1, а
![]() .
.
Таблица 1
|
|
|
|
|
|
|
|
|
Для операций
масштабирования и поворота матрицы
представлены
в табл. 2 и табл. 3 соответственно,
где
![]() ,
,
![]() —
масштабные множители,
—
угол поворота.
—
масштабные множители,
—
угол поворота.
Удобство (1) объясняется тем, что любую комбинацию элементарных преобразований можно описать формулой (1). Например, выражение для сдвига с одновременным поворотом имеет вид
![]()
где
![]() ,
,
![]() —
матрица сдвига,
—
матрица сдвига,
![]() —
матрица поворота.
—
матрица поворота.
Таблица 2
|
|
|
|
|
|
|
|
|
Таблица 3
|
|
|
|
|
|
|
|
|
Представление
графических элементов в растровой форме
требуется для отображения этих элементов
на битовую карту растровой видеосистемы.
Пусть требуется развернуть отрезок
![]() прямой
прямой
![]() ,
причем
,
причем
![]() (при
других значениях
рассматриваемый
ниже алгоритм остается справедливым
после определенных модификаций). Введем
обозначения:
(при
других значениях
рассматриваемый
ниже алгоритм остается справедливым
после определенных модификаций). Введем
обозначения:
![]()
![]() за
величину дискрета (пиксела) примем
единицу. В алгоритме развертки номера
строк и столбцов карты, на пересечении
которых должны находиться точки отрезка,
определяются следующим образом:
за
величину дискрета (пиксела) примем
единицу. В алгоритме развертки номера
строк и столбцов карты, на пересечении
которых должны находиться точки отрезка,
определяются следующим образом:
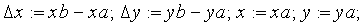
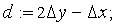
если
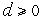 ,
то
,
то
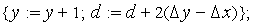 иначе
иначе
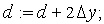
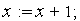
переход к пункту 3, пока не достигнута точка .
Экономичность этого алгоритма обусловливается отсутствием длинных арифметических операций типа умножения.
Выделение окна требуется при определении той части сцены, которая должна быть выведена на экран дисплея.
Пусть окно ограничено
линиями
![]() (рис. 1).
Поочередно для каждого многоугольника
проверяется расположение его вершин и
ребер относительно границ окна. Так,
для многоугольника
(рис. 1).
Поочередно для каждого многоугольника
проверяется расположение его вершин и
ребер относительно границ окна. Так,
для многоугольника
![]() (см.
рис. 1) при отсечении по границе
(см.
рис. 1) при отсечении по границе
![]() просматривается
множество вершин в порядке обхода по
часовой стрелке. Возможны четыре ситуации
для двух последовательных вершин
и
:
просматривается
множество вершин в порядке обхода по
часовой стрелке. Возможны четыре ситуации
для двух последовательных вершин
и
:
если
 и
и
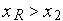 ,
то обе вершины и инцидентное им ребро
находятся вне окна и исключаются из
дальнейшего анализа;
,
то обе вершины и инцидентное им ребро
находятся вне окна и исключаются из
дальнейшего анализа;
если
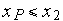 и
и
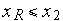 ,
то обе вершины и инцидентное им ребро
остаются для дальнейшего анализа;
,
то обе вершины и инцидентное им ребро
остаются для дальнейшего анализа;
если и , то вершина остается в списке вершин, а вершина заменяется новой вершиной с координатами
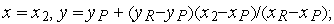 в нашем примере такой новой вершиной
будет
;
в нашем примере такой новой вершиной
будет
;
если и , то вершина заменяется новой вершиной с координатами
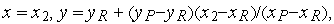 а
вершина
остается
в списке вершин; в нашем примере новой
вершиной будет
а
вершина
остается
в списке вершин; в нашем примере новой
вершиной будет
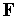 .
.
После окончания просмотра применительно ко всем границам в окне оказываются оставшиеся в списке вершины.
|
Рис. 1. Выделение окна
Применяя эти
правила в нашем примере, получаем сначала
многоугольник
![]() ,
а после отсечения по верхней границе
,
а после отсечения по верхней границе
![]() —
многоугольник
—
многоугольник
![]() (см.
рис. 1). Однако правильный результат
несколько иной, а именно многоугольник
(см.
рис. 1). Однако правильный результат
несколько иной, а именно многоугольник
![]() .
Этот правильный результат получается
при двойном обходе вершин сначала по
часовой стрелке, затем против с включением
в список новых вершин, появляющихся при
каждом обходе.
.
Этот правильный результат получается
при двойном обходе вершин сначала по
часовой стрелке, затем против с включением
в список новых вершин, появляющихся при
каждом обходе.
Применяют ряд
алгоритмов удаления
скрытых линий.
Один из наиболее просто реализуемых
алгоритмов — алгоритм z-буфера, где
z-буфер
— область памяти, число ячеек в которой
равно числу пикселов в окне вывода.
Предполагается, что ось
![]() направлена
по нормали к видовой поверхности и
наблюдатель расположен в точке
направлена
по нормали к видовой поверхности и
наблюдатель расположен в точке
![]() .
.
В начале исполнения алгоритма все пикселы соответствуют максимальному значению , т.е. максимальному удалению от наблюдателя, что приводит к помещению во все ячейки z-буфера значений пикселов фона картины (чертежа). Далее поочередно для всех точек граней рассчитываются значения координаты . Среди точек, относящихся к одному и тому же пикселу (одной и той же ячейке z-буфера ), выбирается точка с наименьшим значением и ее код (т.е. цвет и яркость) помещается в . В итоге z-буфер будет содержать пикселы наиболее близких к наблюдателю граней.
Алгоритмы построения
проекций преобразуют трехмерные
изображения в двумерные. В случае
построения центральной проекции каждая
точка трехмерного изображения отображается
на картинную поверхность путем пересчета
координат
и
(рис. 2).
Так, координату
![]() точки
точки
![]() вычисляют
по очевидной формуле
вычисляют
по очевидной формуле
![]()
аналогично
рассчитывается координата
![]() точки
.
точки
.
|
Рис. 2. Построение центральной проекции точки A
В параллельных
проекциях
![]() и
координаты
и
точек
и
совпадают.
Поэтому построение параллельных проекций
сводится к выделению окна, при необходимости
к повороту изображения и возможно к
удалению скрытых линий.
и
координаты
и
точек
и
совпадают.
Поэтому построение параллельных проекций
сводится к выделению окна, при необходимости
к повороту изображения и возможно к
удалению скрытых линий.
Моделирование
эффектов отражения света от поверхности
объекта в геометрических моделях
называют рендерингом.
Закраска матовых поверхностей основана
на законе Ламберта, согласно которому
яркость отраженного от поверхности
света пропорциональна
![]() ,
где
—
угол между нормалью к поверхности и
направлением луча падающего света. В
алгоритме
Гуро
яркость внутренних точек рассматриваемой
поверхности определяется линейной
интерполяцией яркости в вершинах
многоугольника. При этом сначала
проводится интерполяция в точках ребер,
а затем по строкам горизонтальной
развертки. Более реалистичными получаются
изображения в алгоритме
Фонга,
основанном на линейной интерполяции
векторов нормалей к поверхности. Один
из алгоритмов рендеринга заключается
в трассировке
лучей
— моделировании прохождения лучей
света между источниками, поверхностями
и наблюдателем.
,
где
—
угол между нормалью к поверхности и
направлением луча падающего света. В
алгоритме
Гуро
яркость внутренних точек рассматриваемой
поверхности определяется линейной
интерполяцией яркости в вершинах
многоугольника. При этом сначала
проводится интерполяция в точках ребер,
а затем по строкам горизонтальной
развертки. Более реалистичными получаются
изображения в алгоритме
Фонга,
основанном на линейной интерполяции
векторов нормалей к поверхности. Один
из алгоритмов рендеринга заключается
в трассировке
лучей
— моделировании прохождения лучей
света между источниками, поверхностями
и наблюдателем.