- •Глава 1. Введение в автоматизированное проектирование
- •1.1. Понятие проектирования
- •1.2. Принципы системного подхода
- •1.3. Уровни проектирования
- •1.4. Стадии проектирования
- •1.5. Модели и их параметры в сапр
- •1.6. Проектные процедуры
- •1.7. Жизненный цикл изделий
- •1.8. Структура сапр
- •1.9. Введение в cals-технологии
- •1.10. Этапы проектирования автоматизированных систем
- •Лекция 2. Техническое обеспечение сапр
- •2.1. Требования к техническому обеспечению сапр
- •2.2. Вычислительные системы для сапр
- •2.2.1. Процессоры эвм
- •2.2.2. Память эвм
- •2.2.3. Мониторы
- •2.2.4. Периферийные устройства
- •2.2.5. Шины компьютера
- •2.3. Типы вычислительных машин и систем
- •2.4. Персональный компьютер
- •2.5. Рабочие станции
- •2.6. Архитектуры серверов и суперкомпьютеров
- •2. В.Н. Дацюк, а.А. Букатов, а.И. Жегуло/ методическое пособие по курсу "Многопроцессорные системы и параллельное программирование". -http://rsusu1.Rnd.Runnet.Ru/tutor/method/m1/content.Html
- •2.7. Примеры серверов
- •2.8. Суперкомпьютеры XXI века
- •Лекция 3. Математическое обеспечение анализа проектных решений
- •3.1. Требования к математическим моделям и методам в сапр
- •3.2. Фазовые переменные, компонентные и топологические уравнения
- •3.3. Основные понятия теории графов
- •3.4. Представление топологических уравнений
- •3.5. Особенности эквивалентных схем механических объектов
- •3.6. Методы формирования математических моделей на макроуровне
- •3.7. Выбор методов анализа во временной области
- •3.8. Алгоритм численного интегрирования систем дифференциальных уравнений
- •3.9. Методы решения систем нелинейных алгебраических уравнений
- •3.10. Методы решения систем линейных алгебраических уравнений
- •1. Alglib User Guide. - http://alglib.Sources.Ru/linequations/general/lu.Php. - Проверено 15.12.2009. Лекция 4. Математическое обеспечение анализа проектных решений
- •4.1. Математические модели для анализа на микроуровне
- •4.2. Методы анализа на микроуровне
- •4.3. Метод конечных элементов для анализа механической прочности
- •4.4. Моделирование аналоговых устройств на функциональном уровне
- •4.5. Математические модели дискретных устройств
- •4.6. Методы логического моделирования
- •4.7. Системы массового обслуживания
- •4.8. Аналитические модели смо
- •4.9. Уравнения Колмогорова
- •4.10. Пример аналитической модели
- •4.11. Модель многоканальной смо с отказами
- •4.12. Принципы имитационного моделирования
- •4.13. Событийный метод моделирования
- •4.14. Краткое описание языка gpss
- •1. Томашевский в., Жданова е. Имитационное моделирование в среде gpss. — м.: Бестселлер, 2003.
- •4.15. Сети Петри
- •1. В.Э.Малышкин. Основы параллельных вычислений. -2003 цит сгга, http://www.Ssga.Ru/metodich/paral1/contents.Html
- •4.16. Анализ сетей Петри
- •1. В.Э.Малышкин. Основы параллельных вычислений. -2003 цит сгга, http://www.Ssga.Ru/metodich/paral1/contents.Html Лекция 5. Геометрическое моделирование и машинная графика
- •5.1. Типы геометрических моделей
- •5.2. Методы и алгоритмы компьютерной графики
- •5.3. Программы компьютерной графики
- •5.4. Построение геометрических моделей
- •5.5. Поверхностные модели
- •1. Семенов а.Б. Программирование графических процессоров с использованием Direct3d и hlsl. -http://www.Intuit.Ru/department/graphics/direct3dhlsl/6/1.Html
- •5.7. Графический процессор
- •1. Пахомов с. Революция в мире графических процессоров // КомпьютерПресс, № 12, 2006.
- •5.8. Шейдеры
- •5.9. Геометрические шейдеры
- •5.10. Унифицированный графический процессор
- •1. Пахомов с. Революция в мире графических процессоров // КомпьютерПресс, № 12, 2006.
- •5.11. Примеры графических процессоров
- •Лекция 6. Математическое обеспечение синтеза проектных решений
- •6.1. Критерии оптимальности
- •6.2. Задачи оптимизации с учетом допусков
- •6.3. Классификация методов математического программирования
- •6.4. Методы одномерной оптимизации
- •6.5. Методы безусловной оптимизации
- •6.6. Подходы к решению задач структурного синтеза
- •6.7. Морфологические таблицы
- •6.8. Альтернативные графы
- •Лекция 7.
- •7.1. Интеллектуальные системы
- •7.2. Планирование процессов и распределение ресурсов
- •7.3. Методы локальной оптимизации и поиска с запретами
- •7.4. Методы распространения ограничений
- •7.5. Эволюционные методы
- •7.6. Простой генетический алгоритм
- •7.7. Кроссовер
- •7.8. Метод комбинирования эвристик
- •1. Норенков и.П. Эвристики и их комбинации в генетических методах дискретной оптимизации// Информационные технологии, 1999, № 1.
- •7.9. Примеры применения генетических методов
- •Лекция 8. Автоматизированные системы в промышленности
- •8.1. Системы erp
- •8.2. Стандарт mrp II
- •8.3. Логистические системы
- •8.4. Системы scm
- •8.6. Производственная исполнительная система mes
- •8.7. Автоматизированное управление технологическими процессами
- •8.8. Программирование для станков с чпу
- •8.9. Системы scada
- •8.10. Типовой маршрут проектирования в mcad
- •8.11. Типы сапр в области машиностроения
- •8.12. Основные функции cad-систем
- •8.13. Основные функции cae-систем
- •8.14. Основные функции cam-систем
- •8.15. Графическое ядро
- •Лекция 9.
- •9.1. Структура cad/cam систем
- •9.2. Машиностроительные сапр верхнего уровня
- •9.3. Маршруты проектирования сбис
- •9.4. Схемотехническое проектирование
- •9.5. Модели логических схем цифровой рэа.
- •9.6. Конструкторское проектирование сбис
- •9.7. Проектирование печатных плат
- •9.8. Назначение языка vhdl
- •Лекция10. Методическое и программное обеспечение автоматизированных систем
- •10.1. Типы case-систем
- •10.2. Спецификации проектов программных систем
- •10.3. Методика idef0
- •10.4. Методика idef3
- •10.5. Методика idef1x
- •10.7. Методика проектирования информационных систем на основе uml
- •10.8. Программное обеспечение case-систем
- •10.9. Интегрированные среды разработки приложений
- •Лекция 11. Технологии информационной поддержки этапов жизненного цикла изделий
- •11.1. Обзор cals-стандартов
- •11.2. Структура стандартов step
- •11.4. Интегрированная логистическая поддержка
- •11.5. Интерактивные электронные технические руководства
- •11.6. Стандарт aecma s1000d
- •11.7. Электронная цифровая подпись
- •11.8. Стандарты управления качеством промышленной продукции
- •Лекция 12. Технологии информационной поддержки этапов жизненного цикла изделий
- •12.1. Программное обеспечение cals-технологий
- •12.2. Язык html
- •12.3. Язык xml
- •12.5. Форматирование Web-страниц
- •12.6. Доступ к xml-документам
- •12.7. Мультиагентные системы
- •12.8. Технология soap
- •12.9. Компонентно-ориентированные технологии
Лекция 3. Математическое обеспечение анализа проектных решений
3.1. Требования к математическим моделям и методам в сапр
Основными требованиями к математическим моделям являются требования адекватности, точности, экономичности.
Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность имеет место, если модель отражает заданные свойства объекта с приемлемой точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели.
Экономичность (вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, далее речь пойдет о характеристиках именно математических моделей, и экономичность будет характеризоваться затратами машинных времени и памяти.
Адекватность
оценивается перечнем отражаемых свойств
и областями
адекватности.
Область адекватности — область в
пространстве параметров, в пределах
которой погрешности модели
остаются в допустимых пределах. Например,
область адекватности линеаризованной
модели поверхности детали определяется
системой неравенств:
![]()
где
![]() ,
,
![]() и
и
![]() —
-я
координата
-й
точки поверхности в объекте и модели
соответственно;
—
-я
координата
-й
точки поверхности в объекте и модели
соответственно;
![]() и
и
![]() —
допущенная и предельно допустимая
относительные погрешности моделирования
поверхности, максимум берется по всем
координатам и контролируемым точкам.
—
допущенная и предельно допустимая
относительные погрешности моделирования
поверхности, максимум берется по всем
координатам и контролируемым точкам.
Отметим, что в большинстве случаев области адекватности строятся в пространстве внешних переменных. Так, область адекватности модели электронного радиоэлемента обычно выражает допустимые для применения модели диапазоны изменения моделируемых температур, внешних напряжений, частот.
Аналогичные требования по точности и экономичности фигурируют при выборе численных методов решения уравнений модели.
3.2. Фазовые переменные, компонентные и топологические уравнения
Исходные уравнения для формирования моделей на макроуровне
Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели. В этом параграфе изложен обобщенный подход к формированию алгоритмических моделей на макроуровне, справедливый для большинства приложений.
Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.
Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, математическая модель элемента (ММЭ) представляется компонентными уравнениями.
Топологические уравнения описывают взаимосвязи в составе моделируемой системы.
В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).
Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.
В перечисленных выше приложениях компонентные уравнения имеют вид:
![]() (1)
(1)
топологические уравнения:
![]() (2)
(2)
где
![]() —
вектор фазовых переменных,
—
время.
—
вектор фазовых переменных,
—
время.
Различают фазовые переменные двух типов, их обобщенные наименования — фазовые переменные типа потенциала (например, электрическое напряжение) и фазовые переменные типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение — связи между однотипными фазовыми переменными в разных компонентах.
Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.
Ниже рассмотрим примеры компонентных и топологических уравнений для разных типов систем.
Электрические системы
В электрических
системах фазовыми переменными являются
электрические напряжения и токи.
Компонентами систем могут быть простые
двухполюсные элементы и более сложные
двух- и многополюсные компоненты. К
простым двухполюсникам относятся
следующие элементы: сопротивление,
емкость и индуктивность, характеризуемые
одноименными параметрами
,
![]() ,
,
![]() .
В эквивалентных схемах эти элементы
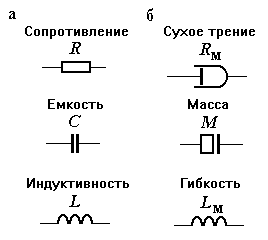
обозначают в соответствии с рис. 1,а.
.
В эквивалентных схемах эти элементы
обозначают в соответствии с рис. 1,а.
Компонентные уравнения простых двухполюсников:
для сопротивления (закон Ома):
![]() (3)
(3)
для емкости:
![]() (4)
(4)
для индуктивности:
![]() (5)
(5)
где
![]() —
напряжение (точнее, падение напряжения
на двухполюснике);
—
ток.
—
напряжение (точнее, падение напряжения
на двухполюснике);
—
ток.
Эти модели лежат в основе моделей других возможных более сложных компонентов. Большая сложность может определяться нелинейностью уравнений (3) — (5) (т.е. зависимостью , , от фазовых переменных), или учетом зависимостей параметров , , от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.
Топологические уравнения выражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:
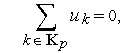 (6)
(6)
 (7)
(7)
где:
![]() —
множество номеров элементов
—
множество номеров элементов
![]() -го
контура;
-го
контура;
![]() —
множество номеров элементов, входящих
в
—
множество номеров элементов, входящих
в
![]() -е
сечение.
-е
сечение.
|
Рис. 1. Компоненты электрических и механических систем
Пример 1
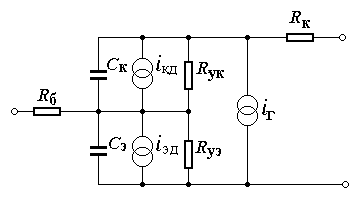
Примером ММ сложного
компонента может служить модель
транзистора. На рис. 2 представлена
эквивалентная схема биполярного
транзистора, на которой зависимые от
напряжений источники тока
![]() и
и
![]() отображают
статические вольтамперные характеристики
p-n переходов,
отображают
статические вольтамперные характеристики
p-n переходов,
![]() и
и
![]() —
тепловые токи переходов,
—
тепловые токи переходов,
![]() —
температурный потенциал,
—
температурный потенциал,
![]() и
и
![]() —
напряжения на эмиттерном и коллекторном
переходах,
—
напряжения на эмиттерном и коллекторном
переходах,
![]() и
и
![]() —
емкости переходов,
—
емкости переходов,
![]() и
и
![]() —
сопротивления утечки переходов,
—
сопротивления утечки переходов,
![]() и
и
![]() —
объемные сопротивления тел базы и
коллектора,
—
объемные сопротивления тел базы и
коллектора,
![]() —
источник тока, моделирующий усилительные
свойства транзистора,
—
источник тока, моделирующий усилительные
свойства транзистора,
![]() и
и
![]() —
прямой и инверсный коэффициенты усиления
тока базы. Здесь
—
прямой и инверсный коэффициенты усиления
тока базы. Здесь
![]() —
фазовые переменные, а остальные величины
— параметры модели транзистора.
—
фазовые переменные, а остальные величины
— параметры модели транзистора.
|
Рис. 2. Эквивалентная схема биполярного транзистора
Механические системы
Фазовыми переменными в механических поступательных системах являются силы и скорости. Используют одну из двух возможных электромеханических аналогий. В дальнейшем будем использовать ту из них, в которой скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока. Учитывая формальный характер подобных аналогий, в равной мере можно применять и противоположную терминологию.
Компонентное уравнение, характеризующее инерционные свойства тел, в силу второго закона Ньютона имеет вид:
![]() (8)
(8)
где
![]() —
сила;
—
сила;
![]() —
масса;
—
поступательная скорость.
—
масса;
—
поступательная скорость.
Упругие свойства тел описываются компонентным уравнением, которое можно получить из уравнения закона Гука. В одномерном случае (если рассматриваются продольные деформации упругого стержня):
![]() (9)
(9)
где
![]() —
механическое напряжение;
—
механическое напряжение;
![]() —
модуль упругости;
—
модуль упругости;
![]() —
относительная деформация;
—
относительная деформация;
![]() —
изменение длины
—
изменение длины
![]() упругого
тела под воздействием
.
Учитывая, что
упругого
тела под воздействием
.
Учитывая, что
![]() ,
где
—
сила,
,
где
—
сила,
![]() —
площадь поперечного сечения тела, и
дифференцируя (9), имеем:
—
площадь поперечного сечения тела, и
дифференцируя (9), имеем:
![]()
или
![]() (10)
(10)
где
![]() —
жесткость (величину, обратную жесткости,
называют гибкостью
—
жесткость (величину, обратную жесткости,
называют гибкостью
![]() ),
),
![]() —
скорость.
—
скорость.
Диссипативные свойства в механических системах твердых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причем в этих соотношениях производные сил или скоростей не фигурируют, как и в случае описания с помощью закона Ома диссипативных свойств в электрических системах.
Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера), во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.
В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных скоростей на угловые, сил — на вращательные моменты, масс — на моменты инерции, жесткостей — на вращательные жесткости.
Условные обозначения простых элементов механической системы показаны на рис. 1,б.
Нетрудно заметить
наличие аналогий между электрической
и механической системами. Так, токам и
напряжениям в первой из них соответствуют
силы (либо моменты) и скорости механической
системы, компонентным уравнениям (4) и
(5) и фигурирующим в них параметрам
и
—
уравнения (8) и (10) и параметры
и
,
очевидна аналогия и между топологическими
уравнениями. Далее параметры
и
будем
называть емкостными (емкостного типа),
параметры
и
—
индуктивными (индуктивного типа), а
параметры
и
![]() —
резистивными (резистивного типа).
—
резистивными (резистивного типа).
Имеется и существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих, соответствующих шести степеням свободы.
Однако отмеченные выше аналогии остаются справедливыми, если их относить к проекциям сил и скоростей на каждую пространственную ось, а при графическом представлении моделей использовать шесть эквивалентных схем — три для поступательных составляющих и три для вращательных.
Гидравлические системы
Фазовыми переменными в гидравлических системах являются расходы и давления. Как и в предыдущем случае, компонентные уравнения описывают свойства жидкости рассеивать или накапливать энергию.
Рассмотрим
компонентные уравнения для жидкости
на линейном участке трубопровода длиной
и
воспользуемся уравнением Навье-Стокса
в следующей его форме (для ламинарного
течения жидкости):
![]()
где
![]() —
плотность жидкости;
—
скорость;
—
плотность жидкости;
—
скорость;
![]() —
давление;
—
давление;
![]() —
коэффициент линеаризованного вязкого
трения. Так как
—
коэффициент линеаризованного вязкого
трения. Так как
![]() ,
где
,
где
![]() —
объемный расход;
—
площадь поперечного сечения трубопровода,
то, заменяя пространственную производную
отношением конечных разностей, имеем:
—
объемный расход;
—
площадь поперечного сечения трубопровода,
то, заменяя пространственную производную
отношением конечных разностей, имеем:
![]()
или
![]() (11)
(11)
Здесь
![]() —
падение давления на рассматриваемом
участке трубопровода;
—
падение давления на рассматриваемом
участке трубопровода;
![]() —
гидравлическая индуктивность, отражающая
инерционные свойства жидкости;
—
гидравлическая индуктивность, отражающая
инерционные свойства жидкости;
![]() —
гидравлическое сопротивление, отражающее
вязкое трение.
—
гидравлическое сопротивление, отражающее
вязкое трение.
Примечание 1
В трубопроводе
круглого сечения радиусом
![]() удобно
использовать выражение для гидравлического
сопротивления при ламинарном течении:
удобно
использовать выражение для гидравлического
сопротивления при ламинарном течении:
![]() ,
где
,
где
![]() —
кинематическая вязкость; в случае
турбулентного характера течения жидкости
компонентное уравнение для вязкого
трения имеет вид
—
кинематическая вязкость; в случае
турбулентного характера течения жидкости
компонентное уравнение для вязкого
трения имеет вид
![]() при
при
 .
.
Интерпретация уравнения (11) приводит к эквивалентной схеме, показанной на рис. 3.
|
Рис. 3. Эквивалентная схема трубопровода
Явление сжимаемости жидкости описывается компонентным уравнением, вытекающим из закона Гука:
![]() (12)
(12)
Дифференцируя
(12) и учитывая, что объемный расход
связан
со скоростью
![]() соотношением
соотношением
![]() ,
получаем:
,
получаем:
![]()
где
![]() —
гидравлическая емкость.
—
гидравлическая емкость.
Связь подсистем различной физической природы
Используют следующие
способы моделирования взаимосвязей
подсистем: с помощью трансформаторной
связи,
гираторной
связи
и с помощью зависимости параметров
компонентов одной подсистемы от фазовых
переменных другой. В эквивалентных
схемах трансформаторные и гираторные
связи представлены зависимыми источниками
фазовых переменных, показанными на
рис. 4. На этом рисунке
—
коэффициент трансформации;
![]() —
передаточная проводимость;
—
передаточная проводимость;
![]() и
и
![]() —
фазовые переменные в
-й
цепи;
—
фазовые переменные в
-й
цепи;
![]() соответствует
первичной, а
соответствует
первичной, а
![]() —
вторичной цепи.
—
вторичной цепи.
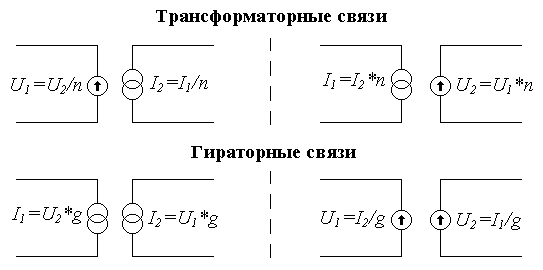
Рис. 4. Трансформаторные и гираторные связи
Примечание 2
Следует отметить, что рассмотренные аналогии фазовых переменных, топологических и компонентных уравнений разных физических систем нашли свое отражение в международном стандарте VHDL-AMS, в котором фазовые переменные типа потенциала названы переменными across quantity, а переменные типа потока — through quantity.