3. Механика твердого тела Основные формулы

Мерой инертности твердого тела при вращательном движении является момент инерции:

I = Σ m_i∙ r_i²,

где m_i – элементарная масса i – го кусочка тела, r_i – расстояние этого кусочка от оси вращения.

Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:

Полый цилиндр I = m ( R₁² + R₂²).

Тонкий обруч I = mR².

Сплошной цилиндр I = mR².

Шар I = mR².

Тонкий стержень I = ml².

Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:

I = I₀ + ma²,

где I – момент инерции тела относительно данной оси, I₀ – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, m – масса тела, а – расстояние между осями.

Основное уравнение динамики вращательного движения твердого тела: I  = M,

где I – момент инерции твердого тела, относительно оси вращения,  – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.

Момент силы F равен: M = F l,

где l – расстояние от линии, вдоль которой действует сила, до оси вращения.

Момент импульса твердого тела относительно неподвижной оси: L = I ω,

где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.

Момент импульса материальной точки относительно неподвижной оси: L = m υ r,

где m – масса частицы, υ – ее скорость, r – расстояние от линии, вдоль которой движется частица, до данной оси.

В замкнутой системе частиц полный момент импульса не меняется: ΣL_i = const.

Кинетическая энергия вращающегося тела:

E_k = ,

где I – момент инерции тела, ω – его угловая скорость.

Кинетическая энергия катящегося тела:

E_k = +,

где m – масса тела, υ₀ – скорость поступательного движения центра масс, I₀ – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.

Примеры решения задач

Задача 13

Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.

Решение

Разобьём конус на цилиндрические слоиось толщиной dr. Масса такого слоя

dm = r²dr,

где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя

dI = dm^.r².

Момент инерции всего конуса складывается из моментов инерции всех слоёв:

I = =ρπ r ⁴ dr = ρR⁵.

Остаётся выразить его через массу всего цилиндра:

m = ==R³,

отсюда ρ = ,

I = = mR².

Задача 14

Маховое колесо, имеющее момент инерции 245 кг∙м², вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

Решение

При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.

ω ₀ = 2 π ν₀, ω = 0,

0 = 2 π ν₀ - ε t,

отсюда ε = .

Это ускорение обусловлено действием момента сил трения

M_тр = I ε = .

Полный угол поворота при равнозамедленном движении находится из соотношения:

φ = ω₀ t- ,

φ =2π N, ω ₀ = 2 π ν₀, ε = .

Перепишем соотношения для угла в виде:

2π N = 2 π ν₀ t - = 2 π ν₀ t - =.

Для нахождения числа оборотов получим:

N = .

Подставив числовые значения, найдём:

M_тр = = 506 Нм,

N = = 600 об.

Задача 15

На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м², намотан шнур, к которому привязан груз массой m = 0,5 кг. До начала вращения высота груза над полом равна h₁ = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.

Решение

Н

R

T

T

m

h₁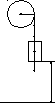

а груз действует сила тяжестиmg и сила натяжения шнура Т. Уравнение поступательного движения груза ma = mg – T.

Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,

где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана, ε = – его угловое ускорение.

TR = I .

Выражаем отсюда силу натяжения шнура:

T = I (10)

и подставляем ее в уравнение движения груза:

mg = a(m + ) = am(1 + ).

Получаем ускорение груза:

a = 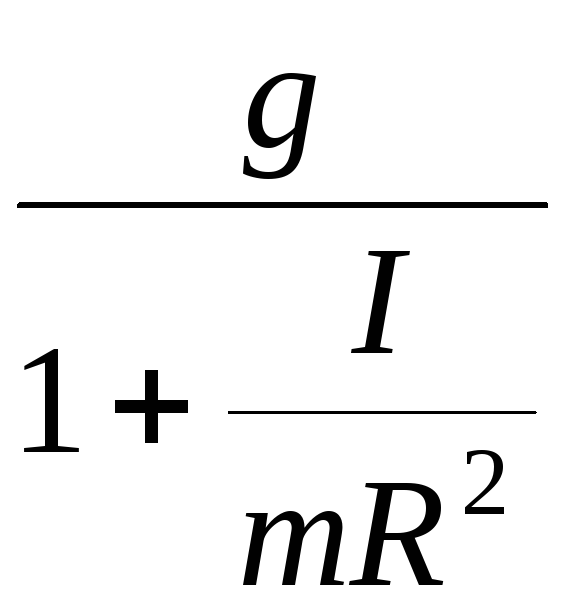. (11)

Время движения груза можно найти из уравнения:

h₁ = ,

t = = .

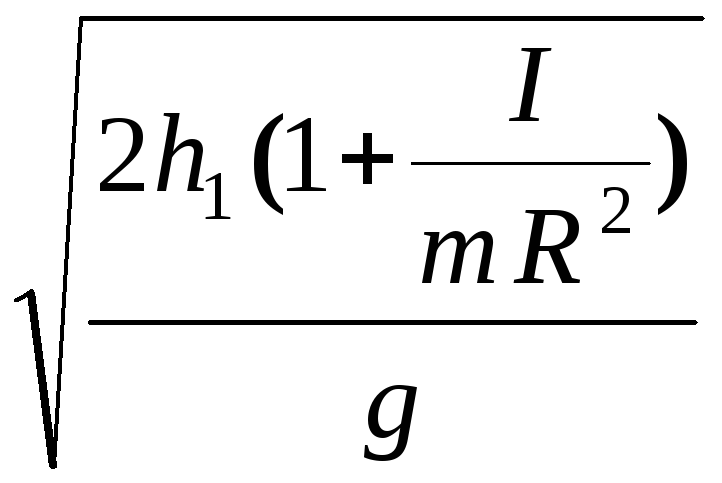В момент удара о пол груз имел скорость:

υ = at = .

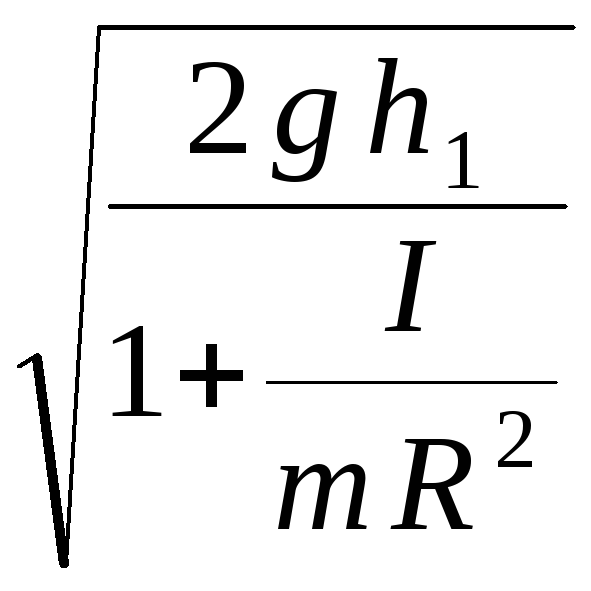Следовательно, его кинетическая энергия:

E_k = =.

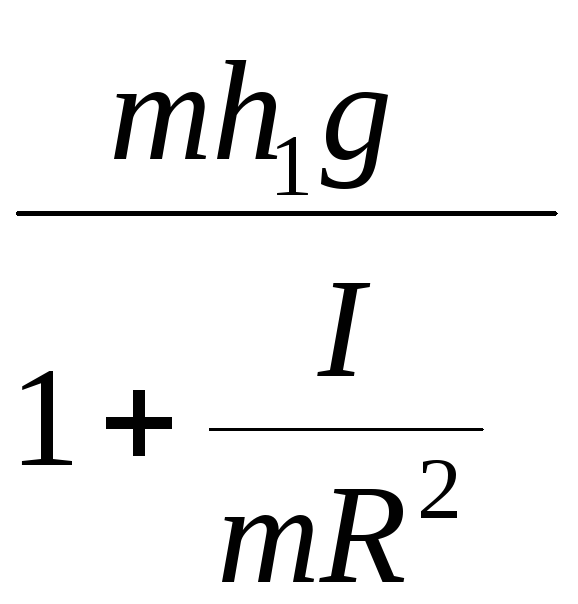Подставив выражение для ускорения (11) в формулу (10), получим: T = = .

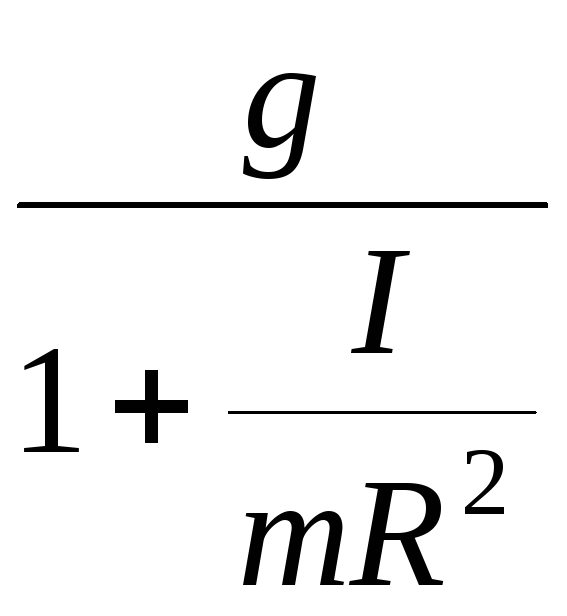Подставив числовые значения, определим искомые величины:

t = = 1,1 c,

E_k = = 0,82 Дж,

T = = 4,1 Н.

Задача 16

Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.

Решение

Кинетическая энергия катящегося тела равна:

E_k = + . (12)

Момент инерции шара I = ,

угловая скорость вращения  = .

Подставляем эти величины в формулу (12):

E_k = + = m υ ².

Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:

Q = E_k1 – E_k2 = m υ₁² - m υ₂² = m(υ₁² - υ₂²).

Подставив числовые значения, получим:

а = ∙1(100∙10^-4 – 64^.10^-4) = 10^-4 = 2,25∙10^-3 Дж = 2,52 МДж.

Задача 17

Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m₁ = 3 кг. Колеса считать тонкими обручами.

Решение

Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.

E_k = + .

Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения  = .

Подставляем эти значения в выражение для кинетической энергии: E_k = + = .

Скорость надо перевести в м/с: υ = 2,5 м/с.

Подстановка числовых значений дает: E_k =253 Дж.

Задача 18

Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

Решение

Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.

Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на

высоту С₂-С₁=l – длина стержня. Стержень приобретает потенциальную энергию Е_n = mgℓ за счет кинетической энергии,

В которую ему сообщили в положении А. Если

υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то

угловая скорость стержня  = .

Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:

I = m l² = m = m l²,

где ml²–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс, – расстояние от центра масс до требуемой оси.

Кинетическая энергия вращательного движения:

E_k = =.= .

По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:

= mgl ,

отсюда υ = .

Подставляем числовые значения: υ = 7 м/с.

Задача 19

Человек массой m₁ = 60 кг находится на неподвижной платформе массой m = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.

Решение

Первоначально платформа с человеком покоилась,

момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы r, в месте нахождения человека u =  r. Таким образом, если человек движется относительно платформы со скоростью

υ, то относительно земли он будет двигаться со скоростью υ –  r, его момент импульса относительно оси платформы L₁ = m₁(υ – r)r. Момент импульса платформы относительно ее оси:

L = – I,

где I – момент инерции платформы.

Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:

I = mR².

Запишем закон сохранения момента импульса для данной системы:

O = L₁ + L = m₁(υ –  r) r – mR²,

отсюда можно определить угловую скорость вращения платформы:

 = .

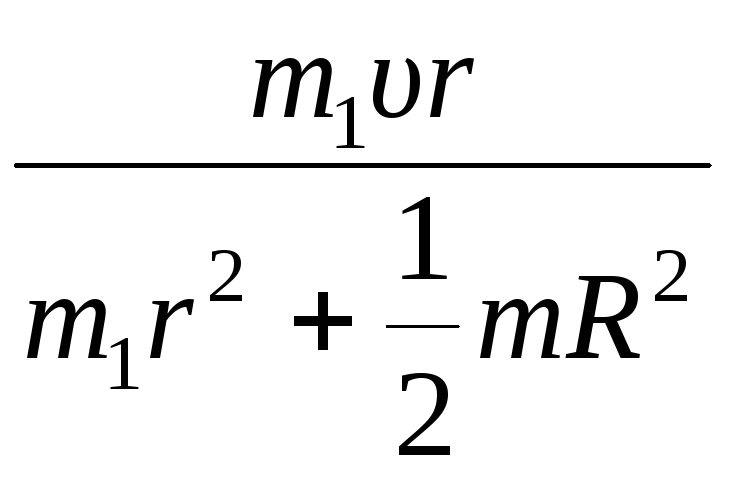Число оборотов платформы в минуту определится из соотношения:

n = 60 = .

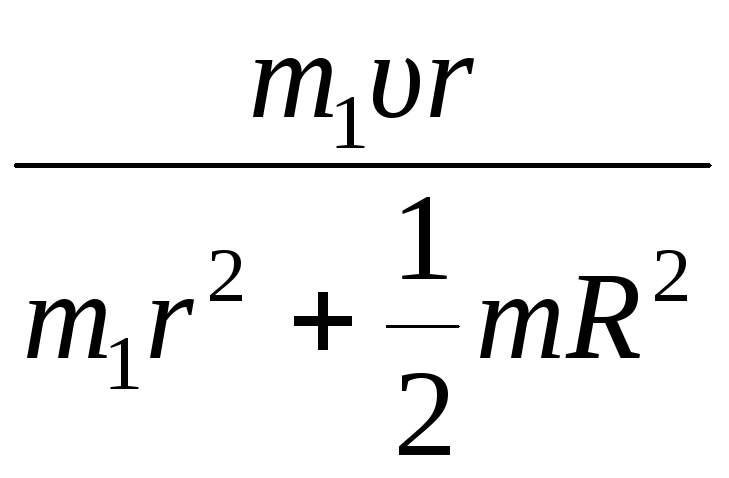Подстановка числового значений дает:

n = 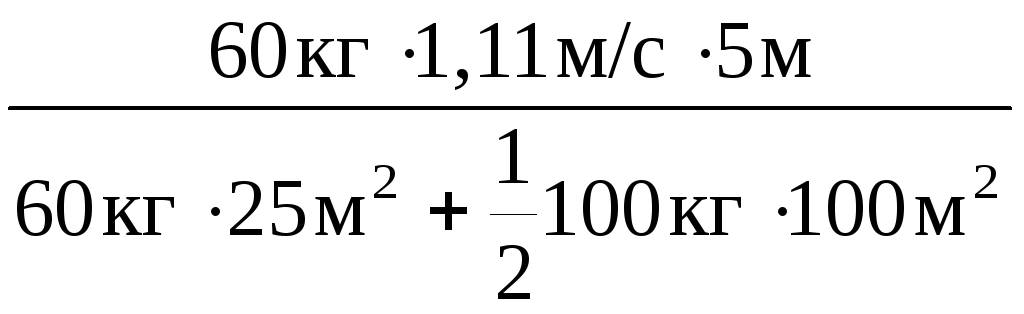= 0,49 об/мин.