ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОСТОВСКИЙ-НА-ДОНУ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ И ИНФОРМАТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению практических работ

по дисциплине

«ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»

Для студентов 2 курсов специальности 23010551

«Программное обеспечение вычислительной техники и автоматизированных систем»

2008

Одобрена цикловой комиссий. Утверждаю

М и ЕН Зам. директора по УР

Протокол №__от______2008г

Председатель ЦК М и ЕН _______________ Жукова Е.Л.

_______________ Лебединская А.Р.

Составитель: Джалагония М.Ш.

Преподаватель высшей категории, РКСИ

Практическая работа №1

«Комплексные числа. Действия комплексными числами в алгебраических формах»

Цель работы: сформировать навыки выполнения математических действий с комплексными числами в алгебраической форме, решения квадратных уравнений с отрицательным дискриминантом.

Теоретическая часть

Комплексными числом z называется выражение вида a+bi, где a и b – действительные числа, а символ i удовлетворяет условию i²=-1.

Число a называется действительной частью комплексного числа и обозначается a=Re z, bi –мнимой частью, b=Im z, i – мнимой единицей.

Множество комплексных чисел обозначается через С. Множество действительных чисел R является подмножеством множества комплексных чисел.

Комплексные числа можно изображать на плоскости по подобию того, как откладываем действительные числа на числовой прямой. На плоскости выберем прямоугольную систему координат Оху. Ось Ох называем действительной осью и будем откладывать на ней действительную часть комплексного числа – a, а на оси Оу—мнимую часть b. Комплексному числу z= a+bi соответствует точка (a;b). Комплексное число z=a+bi можно изобразить и с помощью радиус—вектора . (см. рис.1)

Рис.1 рис.2

Два комплексных числа z₁=a₁+b₁i и z₂=a₂+b₂i называются равными, если соответственно равны их действительные части и коэффициенты при мнимой единице, т. е. a₁=a₂, b₁=b₂. (1)

Комплексное число равно нулю тогда и только тогда, когда a=b=0.

Число называется комплексно-сопряженным с комплексным числом z=a+bi. (См. рис.2). Число –a-bi называется противоположным числу a+bi. (рис.2)

Сумма z комплексных чисел z₁=a₁+b₁i и z₂=a₂+b₂i определяется как комплексное число

z=z₁+z₂=(a₁+a₂)+(b₁+b₂)i. (2)

Сумму комплексных чисел можно найти и как сумму соответствующих векторов и . (рис.3)

Вычитание двух комплексных чисел определяется как операция, обратная сложению.

Z=z₁-z₂=(a₁-a₂) +(b₁-b₂)i. (3)

Геометрически вычитание комплексных чисел сводится к вычитанию соответствующих векторов. (Рис.4)

Рис.3 рис.4

Умножение двух комплексных чисел определяется следующим образом:

z_1∙z₂=(a₁a₂-b₁b₂)+(a₁b₂+a₂b₁)i. (4)

Чтобы выполнить деление комплексных чисел, необходимо умножить делимое и делитель на сопряженное делителю.

. (5)

Возведение комплексного числа в степень n рассматривается как частный случай умножения комплексных чисел.

i²=-1, i³=-i, i⁴=1, i⁵=i, i⁶=-1, i⁷=-i, i⁸=1.

И вообще i⁴ⁿ=1, i⁴ⁿ⁺¹= i, i⁴ⁿ⁺²=-1, i⁴ⁿ⁺³=-i. (6)

Практическая часть

Пример 1. Даны числа: z₁=2+3i, z₂=5-2i. Найти z₁+z₂, z₁+z_2, z₁z₂, z₁/z₂.

Решение.

z₁+z₂=(2+3i) +(5-2i)=2+3i+5-2i=7+i.

z₁+z₂=(2+3i)-(5-2i)=2+3i-5+2i=-3+5i.

z₁z₂=(2+3i)(5-2i)=10-4i+15i-6i²=10+11i+6=16+11i.

Пример 2. Найти x и y из равенства: 3y+5xi=15-7i, где

Решение.

Из условия равенств комплексных чисел имеем: 3y=15; 5x=-7.

y =5;

Ответ: y =5; x =-1,4.

Пример 3. Вычислить: i³⁴+i²³-i¹⁷.

Решение: воспользуемся формулами (6)

i³⁴+i²³-i¹⁷= i^4∙8+2+i^4∙5+3-i^4∙4+1= -1-i-i=-1-2i.

Ответ: -1-2i.

Пример 4. Решить квадратное уравнение: x²+3x+4=0.

Решение

x²+3x+4=0,

D=9-16= -7,

,

Ответ: ,

Практические задания

1. Найдите действительные числа х и у из уравнения.

2. Вычислите z₁+z₂; z₁-z₂; z₁z₂; z₁/z₂. Ответ изобразите на комплексной плоскости.

3. Вычислите.

4. Вычислите.

5. Решить уравнение.

1 вариант (1+i)x+(2+i)y=5+3i. i45+i6-i-4. z1= -4+3i, z2=7-2i. х2-10х+34=0.	вариант (1+2i)x+(3-5i)y=1-3i. i54+i35+i-2. z1=4-3i, z2=-3+6i. 5) 5х2-2х+2=0.
вариант 2x+(4-5i)y= 4x-6i. i12-i36+i -8. z1=-12+2i, z2= 3+4i. 2х2-2х+5=0	вариант (4-3i)x+(1-5i)y=3x+3i. i-12+i45+i67. z1=12-5i, z2=-3+11i. х2+4х+53=0.
вариант z1= 14+i, z2=-1-2i. х2 +4х+29=0.	6 вариант z1= 4-2i, z2=3+2i. х2+2х+2=0.
7 вариант z1= 7+2i, z2=2-8i. х2-2х+5=0.	8 вариант z1= -10+3i, z2=1+2i. х2+4х+13=0.
9 вариант z1= 6+i, z2=-7+4i. 2х2-2х+5=0.	10 вариант z1= -5+7i, z2=-1-4i. z2-z+5=0
вариант z1= 8+3i, z2=3-2i. z2+8z+41=0	вариант z1= 2+4i, z2=-5-2i z2-z+5=0
вариант z1= 5-6i, z2=9-3i. z2-2z+8=0	вариант z1=- 1+3i, z2=5-4i. z2-4z+5=0

Контрольные вопросы

1. Дайте определение мнимой единицы.

2. Как вычислить степень мнимой единицы?

3. Какое число называется комплексным?

4. Какие комплексные числа называются равными? Сопряженными?

5. Как геометрически изображаются комплексные числа?

6. Как выполняются сложение, вычитание, умножение, деление комплексных чисел в алгебраической форме?

Практическая работа № 2

« Переход от алгебраической формы КЧ в тригонометрическую и показательную и обратно. Действия над комплексными числами, заданными в тригонометрической форме»

Цель: сформировать навыки перевода комплексного числа из алгебраической формы в тригонометрическую и показательную и обратно. Развить навыки нахождения произведения, частного, степени, извлечения корня кч в тригонометрической форме.

Теоретическая часть

От алгебраической формы z=a+bi комплексного числа можно перейти к тригонометрической

z=r(cos φ+i sin φ), (1)

и показательной

(2)

где – модуль комплексного числа, длина соответствующего ему вектора ;

Множество всех чисел z, для которых , представляет собой круг радиусом r с центром в начале координат.

Множество всех чисел z, для которых , представляет собой окружность радиусом r с центром в начале координат.

φ – аргумент комплексного числа (угол, который образует вектор с положительным направлением оси абсцисс).

(2)

Пусть даны два комплексных числа в тригонометрической форме:

z₁= r₁(cos φ₁+i sin φ₁); z₂= r₂(cos φ₂+i sin φ₂).

1. При умножении комплексных чисел их модули перемножаются, а аргументы складываются.

z₁z₂=r₁r₂[cos(φ₁+φ₂)+i sin(φ₁+φ₂)].

2. При делении комплексных чисел их модули делятся, а аргументы вычитаются.

z₁/z₂=r₁/r₂[cos(φ₁-φ₂)+i sin(φ₁-φ₂)].

3. При возведении комплексного числа в степень n модуль этого числа возводится в степень n, а аргумент умножается на n.

zⁿ=rⁿ(cos φn+i sin φn).

Данная формула называется формулой Муавра.

4. Для любого z≠0 извлечение корня n-й степени, n≥2, из числа z всегда возможно и имеет n различных значений.

,

где k=0, 1, 2,…, n-1.

Практическая часть

Пример 1. Даны комплексные числа

а) z=3-3i; б) z=-7.

Найдите Re z, Im z, , argz.

Решение. а) z=3-3i.

Re z=a=3; Im z=b=-3;

Т.к. a>0, b<0, то

???

Пример 2. Записать комплексное число в тригонометрической и показательной формах.

Решение.

1) Находим модуль комплексного числа. a=-2, .

2) Находим аргумент комплексного числа.

Так как действительная часть числа отрицательна (a<0), а мнимая часть положительна (b>0), то это число лежит во второй четверти и, следовательно

3) Запишем комплексное число в тригонометрической форме

4) Запишем комплексное число в показательной форме

Пример 3. Записать в тригонометрической и показательной формах комплексные числа: -1; 2i.

а) z=-1.

1) a=-1, b=0, r=1.

2) Данное число лежит на отрицательной полуxоси Ох (рис.2), следовательно, φ=180⁰.

3) -1=cos 180⁰+i sin 180⁰.

б) z=2i.

1) a=0, b=2, r=2

2) Данное число лежит на положительной полуоси ординат (рис.2), следовательно, =90⁰.

3) 2i =2(cos 90⁰+i sin 90⁰).

Пример 4. Умножить числа , z.

Решение.

Пример 5. Вычислить , если , .

Решение.

.

.

Пример 6. Вычислить: .

Решение

Запишем число в тригонометрической форме:

.

По формуле Муавра находим _.

Пример 7. Найти все значения .

Решение

Так как , то

Придавая k последовательно значения 0, 1, 2, 3 соответственно, получим:

при k=0 ;

при k=1 ;

при k=2 ;

при k=3 z;

Ответы отмечены на комплексной плоскости.

Практические Задания

Вариант 1 Построить точки, изображающие комплексные числа: -5; 3i; -2+i. Запишите их в тригонометрической показательной формах. Вычислить: . Вычислить: . Возвести в степень: ; Извлечь корень: .	Вариант 2 Построить точки, изображающие комплексные числа -3; -3i; 1- i. Запишите их в тригонометрической показательной формах. Вычислить: 3(cos 100+i sin 100)∙7(cos 350+isin 350). Вычислить: Возвести в степень: . Извлечь корень: .
Вариант 3 Построить точки, изображающие следующие комплексные числа: -5, 2i, -2+2i. Запишите их в тригонометрической показательной формах. Вычислить: . Вычислить: . Возвести в степень: . Извлечь корень: .	Вариант 4 Построить точки, изображающие следующие комплексные числа: 4, -3i, 3+2i, -2-2 i. Запишите их в тригонометрической показательной формах. Вычислить: . Вычислить: Возвести в степень: . Извлечь корень: .
Вариант 5 Построить точки, изображающие следующие комплексные числа: 4, 6i, 3-3 i. Запишите их в тригонометрической и показательной формах. Вычислить: . Вычислить: 4. Возвести в степень: 5.Извлечь корень: .	Вариант 6 Построить точки, изображающие следующие комплексные числа: -6, 2i, -4+4i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .
Вариант 7 Построить точки, изображающие следующие комплексные числа: 2,5; -4i; -2+ i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .	Вариант 8 Построить точки, изображающие следующие комплексные числа: 7; -2,5i; 2i+2. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .
Вариант 9 Построить точки, изображающие следующие комплексные числа: 2; -3i; . Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .	Вариант 10 Построить точки, изображающие следующие комплексные числа: -5; 4i; 6-6i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .
Вариант 11 Построить точки, изображающие следующие комплексные числа: -2; 5i; 7 -7i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: 5.Извлечь корень: .	Вариант 12 Построить точки, изображающие следующие комплексные числа: -4; 3i; -1+ i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: Возвести в степень: Извлечь корень: .
Вариант 13 Построить точки, изображающие следующие комплексные числа: 1; -i; 2-2i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: . 5.Извлечь корень: .	Вариант 14 Построить точки, изображающие следующие комплексные числа: -3; 4i; - -i. Запишите их в тригонометрической и показательной формах. Вычислить: Вычислить: 4. Возвести в степень: . 5.Извлечь корень: .

Практическая работа №3

«Операции над матрицами. Вычисление определителей»

Цель работы: Научится выполнять линейные операции над матрицами, умножать матрицы, находить ранг матрицы методом элементарных преобразований.

Теоретическая часть

Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов

.

Матрицу также можно записать вкратце , где --- номер строки, ---номер столбца, называются элементами матрицы, элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.

Если число строк и столбцов равны (т.е. m=n), то матрица называется квадратной:

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной:

Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной: .

Матрица, все элементы которой равны нулю, называется нулевой:

Матрица, содержащая одну столбец или один строку, называется вектором (их также называют вектор-столбец и вектор-строка соответственно):

, .

Если строки данной матрицы поменять на столбцы с тем же номером, то получим так называемую транспонированную матрицу. Например, если , по .

Действия над матрицами.

Сложение. Суммой двух матриц и называется матрица

, где . Следует отметить, что складывать можно только матрицы одинаковых размеров.

Свойства сложения матриц:

1. А+В=В+А (коммутативность).

2. (А+В)+С=А+(В+С) (ассоциативность).

Умножение на число. Произведением матрицы на число k, называется матрица , где

Свойства умножения матриц на число:

1. (ассоциативность).

2. ( дистрибутивность относительно сложения матриц).

3. ( дистрибутивность относительно сложения чисел).

Линейной комбинацией матриц A и B одинакового размера называется выражение , где --произвольные числа.

Умножение матриц. Умножать можно матрицы, в которых число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы на называется матрица такая, что

, где , .

Свойства умножения матриц.

1. (ассоциативность).

2. ( дистрибутивность).

3. Произведение матриц АВ не всегда равно произведению матриц ВА— ( отсутствие коммутативности)

Коммутативными называются матрицы А и В, если АВ=ВА.

Каждой квадратичной матрице можно сопоставить число detA, которое называется определителем или детерминантом и вычисляется следующим образом:

• Определителем второго порядка, соответствующим матрице , называется число

_.

• Определителем третьего порядка, соответствующим матрице , называется число

Определитель третьего порядка можно также вычислить по формуле:

_.

Свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух параллельных строк (или столбцов) определитель меняет знак.

3. Определитель, имеющий два одинаковых столбца или строку, равен нулю.

4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

5. Если элементы какого-либо ряда определителя представляет сумму слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженное на любое число.

7. Определитель равен сумме произведения элементов некоторого ряда на соответствующие им алгебраические дополнения.

8. Сумма произведения элементов какого-либо ряда определителя на алгебраическое дополнение соответствующих элементов параллельного ряда равна нулю.

Практическая часть

Пример 1. Найдите линейную комбинацию 3А-4В, если

.

Решение.

Пример 2. Найдите произведения АВ (если это возможно):

а) , . б) , .

в) ,

Решение. а) Число столбцов первой матрицы равно числу строк второй матрицы, поэтому выполнить произведение АВ возможно и оно равно:

б)

в) Произведение АВ невозможно, т.к. число столбцов первой матрицы не равно числу строк второй матрицы ( ).

Пример 3. Вычислите определители:

а) ; б) .

Решение. а)

б) 1 способ.

2 способ.

.

Практические задания

Даны две матрицы А и В.

1. Найдите: а) линейную комбинацию матриц 2А+3В-Е, где Е – единичная матрица.

б) произведение матриц АВ.

2. докажите, что det(AB)=detA^.detB

Вариант 1 ,	Вариант 2 ,
Вариант 3 ,	Вариант 4 ,
Вариант 5 ,	Вариант 6 ,
Вариант 7 ,	Вариант 8 ,
Вариант 9 ,	Вариант 10 ,
Вариант 11 , ,	Вариант 12 ,
Вариант 13 ,	Вариант 14 ,

Контрольные вопросы:

1. Что называется матрицей?

2. Какие виды матриц Вы знаете?

3. Какие операции называются элементарными преобразованиями?

4. Какие матрицы можно перемножить?

5. Можно ли умножить квадратную матрицу на неквадратную?

6. Если две матрицы можно складывать, можно ли их умножать?

7. Если две матрицы можно умножать, можно ли их умножать?

8. Какие матрицы называются эквивалентными?

9. Что называется ранг матрицы?

10. Сформулируйте алгоритм нахождения ранга матрицы.

Практическая работа №4

« Обратная матрица. Ранг матрицы»

Цель работы: Научится находить определители второго и третьего порядка, обратные матрицы.

Теоретическая часть

Миноры и алгебраические дополнения.

Минором некоторого элемента a_ij определителя n-него порядка называется определитель n-1-го порядка, полученный из исходного путём вычеркивания строки и столбца, на пересечений которых находится данный элемент. Минор обозначается M_ij.

Алгебраическим дополнением элемента a_ij определителя называется его минор, взятый со знаком «плюс», если сумма i+j четная и со знаком «минус», если эта сумма нечетная.

С помощью алгебраического дополнения можно вычислить определитель n-го порядка:

detA=a₁₁A₁₁+a₁₂A₁₂+…+a_1n-1A_1n-1+a_1nA_1n

Обратная матрица.

Квадратная матрица называется невырожденной, если ее определитель не равен нулю, т.е. . В противном случае матрица А называется вырожденной.

Матрицей, обратной квадратной матрице А называется матрица А^-1, такая, что А^-1А=Е, где Е—единичная матрица.

Если матрица А невырожденная, то

, где --транспонированная матрица к матрице А.

Алгоритм нахождения обратной матрицы:

1. Найти определитель матрицы. (Если detA=0, то обратной матрицы не существует).

2. Найти алгебраические дополнения ко всем элементам матрицы.

3. Записать транспонированную матрицу (A_ij)^T.

4. Найти по формуле обратную матрицу.

5. Сделать проверку.

Ранг матрицы

Рассмотрим прямоугольную матрицу размера . Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А.

Среди всех отличных от нуля миноров матрицы А найдется, по крайней мере, один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего, чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

Ранг матрицы можно найти методом элементарных преобразований.

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число,

4) вычеркивание нулевой строки.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так:

A  B.

Матрица имеет ступенчатый вид, если в каждой ее строке стоит нулей больше, чем в предыдущей. При этом учитываются лишь нули, стоящие в начале строки до первого ненулевого числа.

Ранг матрицы равен количеству ненулевых строк матрицы после приведения ее с помощью элементарных преобразований к ступенчатому виду.

Практическая часть

Пример 1. Найдите матрицу, обратную к данной:

а) б)

Решение. а) Решаем по алгоритму:

1. 

т.к. , то А^-1 существует.

2. Алгебраические дополнения:

3. Матрица A_ij имеет вид:

. Транспонируем ее:

4. Обратная матрица имеет вид:

5. Делаем проверку:

б) Найдем определитель матрицы

. Матрица вырожденная, следовательно, матрица А^-1 не существует.

Пример 2. Найти ранг матрицы  

Решение. Приведем матицу к ступенчатому виду. Из второй строки вычтем первую и переставим эти строки: .Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5: ; из третьей строки вычтем первую; получим матрицу , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2.

Ответ: r(A)=2.

Практические задания

Даны матрицы А и В. Найдите:

a) матрицу, обратную матрице А.

Вариант 1 ,	Вариант 2 ,
Вариант 3 ,	Вариант 4 ,
Вариант 5 ,	Вариант 6 ,
Вариант 7 ,	Вариант 8 ,
Вариант 9 ,	Вариант 10 ,
Вариант 11 , ,	Вариант 12 ,
Вариант 13 ,	Вариант 14 ,

Контрольные вопросы:

1. Формулы нахождения определителей второго и третьего порядков.

2. Перечислите свойства определителей.

3. Что называется минором матрицы?

4. Что называется алгебраическим дополнением матрицы?

5. Что называется транспонированной матрицей?

6. Что называется обратной матрицей?

7. Сформулируйте алгоритм нахождения обратной матрицы.

8. Какая матрица называется вырожденной? Невырожденной?

Практическая работа №5

«Решение системы линейных уравнений»

Цель: научить решать системы уравнений по правилу Крамера, методом Гаусса, матричным способом.

Теоретическая часть

1. Правило Крамера.

Пусть дана система n линейных алгебраических уравнений с n неизвестными вида

Система уравнений называется совместной, если она имеет хотя бы единственное решение, и несовместное, если она не имеет ни одного решения. Если система уравнений совместна, то корни можно найти по формуле Крамера:

В этих формулах ∆--определитель системы, а ∆_i—определитель, полученный из определителя системы заменой i-го столбца столбцом свободных членов.

При этом нужно помнить, что

а) если ,то система имеет единственное решение.

б) если ,то система имеет бесконечное множество решений.

в) если , то система не имеет решений.

2. Матричный способ.

Систему можно представить в матричном виде—в виде матричного уравнения АХ=В, где

, , .

Матрица А, элементами которой являются коэффициенты стоящие перед неизвестными, называются матрицей системы. Матрица—столбец В, элементами которой являются правые части уравнений системы, называется матрицей правой части. Матрица—столбец Х, элементы которой — искомые неизвестные, называется решением системы.

Решение матричного уравнения при условий, что , имеет вид

,

где А^-1—матрица, обратная к матрице А.

3. Метод Гаусса.

Данный метод называется и методом исключения неизвестных.

Алгоритм решения:

• Составить расширенную матрицу

• С помощью элементарных преобразований привести матрицу к ступенчатому виду;

• Составить соответствующую систему уравнений;

• Решить уравнения, начиная с последнего.

Пример 1. Решить систему по формулам Крамера

Решение. Найдём определители .

Мы имеем дело со случаем 3, следовательно, система не имеет решений.

Пример 2. Решить систему уравнений по формулам Крамера

Решение. Формулы Крамера имеют вид:

, .

,

Ответ: .

Пример 3. Решите систему матричным способом.

Решение. Найдем матрицу, обратную. к матрице А.

Алгебраические дополнения:

Найдем обратную матрицу: .

Найдем Х:

.

Ответ: (-1;0;1).

Пример 4. Решить систему методом Гаусса.

Решение. Выпишем расширенную матрицу:

_{Поменяем местами первую и вторую строчки}

Умножим первую строчку на -2 и вычтем со второй строчкой, результат запишем на место второй строчки, а первую строчку перепишем без изменения:

~

Первую строчку умножим на -3 и сложим ее с третьей строчкой и результат запишем вместо третьей строчки, первую и вторую строчки оставим без изменения:

~ ~ ~ .

Данная матрица соответствует системе уравнений

Решаем уравнения, начиная с последнего

_z=1; ; .

Ответ: (-1;0;1).

Практические задания

Решите систему уравнений (1): а) по формулам Крамера;

б) матричным способом;

Решите систему уравнений (2): а) по формулам Крамера;

б) матричным способом;

в) методом Гаусса

Вариант 1 1) 2)	Вариант 2 1) 2)
Вариант 3 1) 2)	Вариант 4 1) 2)
Вариант 5 1) 2)	Вариант 6 1) 2)
Вариант 7 1) 2)	Вариант 8 1) 2)
Вариант 9 1) 2)	Вариант 10 1) 2)
Вариант 11 1) 2)	Вариант 12 1) 2)
Вариант 13 1) 2)	Вариант 14 1) 2)

Контрольные вопросы:

1. Какие системы уравнений называются совместной? Несовместной?

2. Формулы Крамера.

3. При каких условиях система имеет одно решение? Бесконечное множество решений? Нет решения.

4. Сформулируйте метод решения систем линейных уравнений методом Гаусса.

5. Сформулируйте метод решения систем линейных уравнений матричным способом.

Практическая работа №6

«Операции над векторами. Скалярное, векторное и смешанное произведение векторов.

Цель работы: Сформировать навыки выполнения операций над векторами, решать прикладные задачи с помощью скалярного, векторного, смешенного произведения векторов.

Теоретическая часть

Любой направленный отрезок называется вектором. Нулевым вектором называется вектор, начало и конец которого совпадают. Например, вектор или является нулевым.

Два вектора называется коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если направление коллинеарных векторов совпадают, то они называются сонаправленными. Если они противоположно направлены, то они называются противоположно направленными.

Суммой векторов и называется вектор , начало которого совпадает с началом первого вектора, а конец --с концом второго вектора, при условий, что начало второго, перенесено в конец первого (рис 1). Можно также сложить два вектора способом параллелограмма (рис 3).

Сложение более двух векторов производится по так называемому правилу многоугольников. Суммой нескольких векторов называется вектор, соединяющий начало первого вектора с концом второго вектора (рис 2).

рис.1 рис. 2

Разностью векторов и называется сумма векторов и ,т.е. .

Свойства суммы векторов:

1. --переместительный закон;

2. --сочетательный закон;

3. .

рис. 3 рис. 4

Вектор можно умножить (и разделить) на скаляр. При этом модуль вектора соответственно умножается (делится) на данное число, а направление результирующего вектора определяется знаком множителя (делителя): если множитель положительный, то направление вектора сохраняется, а если множитель отрицательный, то направление вектора меняется на противоположное.   На рисунке 5 изображён результат умножения вектора на 2: направление вектора не изменилось, модуль увеличился в 2 раза. При делении вектора на

-2 его направление изменилось на противоположное, а модуль уменьшился в два 2 раза.

Рис 5.

Произведением вектора на вещественное число k называется вектор , который имеет длину , и коллинеарен вектору , при этом если k>0, то векторы и ; а если k<0, то векторы и противоположно направлены.

Свойства умножения векторов:

1. --переместительный закон (коммутативность);

2. --сочетательный закон (ассоциативность);

3. --распределительный закон (дистрибутивность).

Любой вектор на плоскости может быть представлен в виде линейной комбинации двух неколлинеарных векторов и , т.е. .

Упорядоченная пара неколлинеарных векторов и на плоскости называется векторным базисом.

Числа x и y называются координатами вектора в базисе .

В пространстве понятие вектора вводится, так же как и на плоскости. Введем новое понятие - компланарные векторы.

Определение: Три и большее число ненулевых вектора в пространстве называются компланарными, если они лежат на прямых, параллельных одной плоскости.

Левая и правая тройки векторов. Тройка некомпланарных векторов , , называется правой, если с конца третьего вектора с кратчайший поворот вектора ко второму вектору виден совершающимся против часовой стрелки и левую, если по часовой стрелке. Все правые (или левые) тройки векторов называются одинаково ориентированными.

Вектор. Базис и координаты. Тройка некомпланарных векторов в R³ называется базисом, а сами векторы - базисными. Любой вектор может быть единственным образом разложен по базисным векторам, то есть представлен в виде

                                                                          

числа x₁, x₂, x₃ в разложении (1.1) называются координатами вектора в базисе и обозначаются (x₁, x₂, x₃).

Вектор. Ортонормированный базис. Если векторы попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x₁, x₂, x₃ - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать .

Будем предполагать, что в пространстве R³ выбрана правая система декартовых прямоугольных координат .

Пусть даны вектора ,

• Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов, т.е.

(1)

• Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов

(2)

• Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.

(3)

Запомните, также, что

• координаты нулевого вектора равны нулю

• координаты равных векторов соответственно равны:

Длину вектора можно вычислить по формуле (4)

Рассмотрим точки A₁ (x₁; y₁; z₁) и A₂ (x₂; y₂; z₂) и найдем расстояние между этими точками.

Расстояние между точками A₁ и A₂ можно вычислить по формуле

(5)

Если нужно найти координаты вектора , то можно пользоваться формулой (5), т.е

(5)^/

или же сначала найти координаты вектора по формуле , а затем воспользоваться формулой (4).

Пусть даны точки А(х₁;у_1;z₁), B(x₂;y₂;z₂), а т.С(х;y;z) является серединой отрезка АВ, тогда

(6).

Координаты точки М, делящей в заданном отношении λ отрезок АВ, находится по формулам:

,

где .

Если λ=1, то получим формулу (6).

Скалярным произведением векторов и называется произведение их длин на косинус угла между ними:

(7)

• Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

• Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

• Скалярное произведение двух векторов , и заданных своими координатами, может быть вычислено по формуле (8)

Перечислим основные свойства скалярного произведения

Для любых векторов ,   и и любого числа λ справедливы равенства:

1. причем _;

2. (переместительный закон).

3. (распределительный закон).

4. (сочетательный закон).

Найдем теперь угол между векторами через их координаты. Мы знаем, что

, откуда . Учитывая имеем

(9)

Рассмотрим два произвольных вектора: и

Векторным произведением вектора на вектор называется третий вектор который обладает следующими свойствами:

1. Его длина равна

2. Вектор перпендикулярен к плоскости, в которой лежат вектора и

3. Векторы , и образуют правую тройку.

Векторное произведение обозначается квадратными скобками или

Свойства векторного произведения:

• векторное произведение произвольного вектора на нулевой вектор равно нулевому вектору;

• векторное произведение двух коллинеарных векторов равно нулевому вектору;

• координаты векторного произведения векторов и следующие

• 

• Если векторы и коллинеарные, то и [ ] = 0, в частности, [ ] = 0. Векторные произведения ортов: , , .

Если векторы и заданы в базисе координатами ,

, то

(10)

Для вычисления площади параллелограмма, построенного на векторах и применяется формула

.

Смешанное произведение. Если векторное произведение двух векторов и скалярно умножается на третий вектор , то такое произведение трех векторов называется смешанным произведением и обозначается символом

_.

Если векторы , и в базисе заданы своими координатами (a₁, a₂, a₃), (b₁, b₂, b₃), (c₁, c₂, c₃), то

(11)

Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.

Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка , , - левая, то <0 и V = - , следовательно, .

Объём треугольной пирамиды, построенной на векторах , и равен:

.

Практическая часть

Пример 1. Зная векторы и вычислите длину высоты AD треугольника ABC.

Решение. Обозначая площадь треугольника ABC через S, получим: . Тогда , где .

Рис.

Площадь можно найти также по формуле

Как видим из рисунка значит, вектор имеет координаты    

,

, откуда .

Пример 2.

Даны координаты вершины пирамиды DАВС. A(5;1;-4), B(1;2;-1), C(3;3;-4), D(2;2;2). Найдите:

1. длины ребер пирамиды AB, DB.

2. углы треугольника ABC;

3. площадь основания;

4. объём пирамиды;

5. высоту пирамиды

Решение.

1. Используем формулу (5)

(можно также применить формулу (5)^/)

2. Найдем координаты векторов .

Воспользуемся формулой (9)

Аналогично находятся остальные углы треугольника:

,

Угол С найдите самостоятельно.

3. Зная, что площадь треугольника ABC равняется половине площади параллелограмма, построенного на векторах и , имеем .

4. Находим объём пирамиды: ;

Согласно формуле (12) имеем:

.

5. Т.к. объём пирамиды V есть , то .

Практические задания

Даны координаты вершины пирамиды DАВС. Найдите:

1. длины ребер пирамиды AB, DB, AC

2. углы треугольника ABC;

3. площадь основания;

4. объём пирамиды;

5. высоту пирамиды.

Вариант 1 А(2;3;-1), B(-2;3;4), C(0;5;7), D(-1;0;3)	Вариант 2 А(2;-3;5), B(-4;7;5), C(11;0;2). D(0;2;5)
Вариант 3 А(-10;3;2), B(3;-4;1), C(0;5;-3). D(2;0;1)	Вариант 4 А(5;-2;-1), B(4;2;3), C(0;-4;1). D(-1;2;1)
Вариант 5 А(12;1;0), B(5;7;-1), C(-3;4;5). D(2;-1;0)	Вариант 6 А(-2;3;4), B(-5;7;1), C(0;-4;2). D(3;-1;2)
Вариант 7 А(2;3;-1), B(-2;3;4), C(0;5;7). D(0;1;2)	Вариант 8 А(2;-3;5), B(-4;7;5), C(11;0;2). D(4;-2;1)
Вариант 9 А(-10;3;2), B(3;-4;1), C(0;5;-3). D(1;2;0)	Вариант 10 А(5;-2;-1), B(4;2;3), C(0;-4;1). D(3;1;-2)
Вариант 11 А(12;1;0), B(5;7;-1), C(-3;4;5). D(1;5;2)	Вариант 12 А(-2;3;4), B(-5;7;1), C(0;-4;2). D(4;-3;0)
Вариант 13 А(2;3;-1), B(-2;3;4), C(0;5;7). D(2;-5;2)	Вариант 14 А(2;-3;5), B(-4;7;5), C(11;0;2). D(3;2;1)

Контрольные вопросы:

1. Что называется вектором? Какие величины являются векторными? Приведите примеры.

2. Какие вектора называются коллинеарными, компланарными?

3. Как найти координаты суммы, разности векторов?

4. Дайте определение скалярного произведения векторов.

5. Перечислите свойства скалярного произведения вектора.

6. Как найти угол между векторами?

7. Какая тройка векторов называется правой, левой?

8. Что называется базисом? Базисными векторами?

9. Что называется ортонормированным базисом?

10. Дайте определение векторного произведения векторов.

11. Какими свойствами обладает векторное произведение векторов?

12. Какой геометрический смысл имеет векторное произведение векторов?

13. Дайте определение смешанного произведения векторов.

14. Какой геометрический смысл имеет смешанное произведение векторов?

Практическая работа №7

«Уравнение прямой на плоскости»

Цель работы: Научится составлять уравнение прямой по заданным условиям, исследовать взаимное расположение прямых, находить угол между прямыми, решать геометрические задачи.

Теоретическая часть

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, есть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:

1⁰. Общее уравнение прямой:

Ax + By + C = 0.                                                          (1)

Вектор (А,В) ортогонален прямой, числа A и B одновременно не равны нулю.

     Частные случаи:

     1) При А=0 имеем: By + C = 0 . Положим , получим y=b -- прямая параллельна оси Ox (рис.1)

2. При В=0 имеем: Ax + C = 0 Положим , получим - прямая параллельна оси Oy (рис.2)

     Рис.1. рис.2.

 3) При С=0 имеем: Ax + By = 0 или где - прямая проходит через начало координат; k-угловой коэффициент прямой. Он равен тангенсу углу наклона прямой к положительному направлению оси Ох.

.

рис.3.

     4) При A=C=0, то y = 0 - ось Ox;

     5) При B=C=0, то x = 0 - ось Oy.

2⁰. Уравнение прямой с угловым коэффициентом:

y - y_o = k (x - x_o),                                                          (2)

где k - угловой коэффициент прямой, M(x_o,y_o) - некоторая точка, принадлежащая прямой.

3⁰. Уравнение прямой в отрезках:

(3)

где a, b - величины отрезков, отсекаемых прямой на осях координат                  

Рис.4 Рис.5.

4⁰. Уравнение прямой, проходящей через две данные точки -  A(x₁, y₁) и B(x₂, y₂ ), где .

Возьмем произвольную точку М(х;у) на прямой (рис.. Т.к. точки М, М₁, М₂ лежат на одной прямой, то векторы и коллинеарные. А из условия коллинеарности следует:

.                                                       (4)

5⁰. Уравнение прямой, проходящей через данную точку М(x₁, y₁) параллельно данному вектору .

Рис. 6 рис.7

На данной прямой возьмем произвольную точку М(х;у) (рис.6). Рассмотрим вектор . Т.к. векторы и коллинеарные, то имеем:

. (5)

6⁰. Уравнение прямой, проходящей через данную точку М(x₁, y₁) с заданным нормальным вектором :

(6)

Данное уравнение отражает условие перпендикулярности векторов и (рис. 7).

Величина угла между прямыми y = k₁x+b и y = k₂x+b₂ задается формулой:

.

Если даны общие уравнения прямых, то угол между ними находим по формуле

, (7)

где и --нормальные векторы прямых.

Взаимное расположение прямых:

Пусть даны уравнения прямых

A₁ x + B₁ y + C₁= 0,                                                       (8)

A₂ x + B₂ y + C₂ = 0,                                                      (9)

Прямые (8) и (9) параллельны, или

пересекаются, или

задают одну и ту же прямую или

перпендикулярны или

Практическая часть

Пример 1. Треугольник АВС задан координатами вершин А(-2;2), В(3;4), С(-2;-3). Составьте уравнения стороны АВ, медианы СМ, высоты АН.

Решение. Построим треугольник АВС. Проведем высоту АН и медиану СМ

У равнение стороны АВ: Используем формулу (4). х₁=-2, х₂=3, у₁=2, у₂=4.

Имеем: _,

2х+4=5у-10, 2х-5у+14=0.

Рис.8 Уравнение медианы СМ: Найдем координаты середины отрезка АВ—т. М(х;у).

Уравнение прямой, проходящей через точки М(0,5;3) и С(-2;-3):

-6х+3=-2,5у+5, -6х+2,5у-2=0, 12х-5у+4=0.

Уравнение высоты: воспользуемся формулой (6). В данном случае нормальный вектор , т.е. А=-5, В=-7, а х₁=-2, у₁=2. Имеем

-5(х+2)-7(у-2)=0, -5х-10-7у+14=0, 5х+7у-4=0.

Ответ: 2х-у+6=0, 12х-5у+4=0, 5х+7у-4=0.

Пример 2. При каком значении параметра t прямые, уравнения которых 2tx-4y+3 = 0 и (1+t)x-ty = 0, параллельны?

Решение. Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е.

_{, ,} , t=2. &&&&&

3t/(1+t) = -8/(-2t). Решая полученное уравнение, находим t: t₁ = 2, t₂ = -2/3.

Ответ: t₁ = 2, t₂ = -2/3.

Пример 3.Найдите острый угол между прямыми 2х-3у+6= и 3х-у-3=0.

Решение. За угол между прямыми возьмем угол их нормальными векторами. Воспользуемся формулой (7).

Ответ:

Пример 4. Составьте уравнение прямой, проходящей через точку М(4;-2) перпендикулярно прямой у=3х-5.

Решение. Запишем данное уравнение в общем виде: 3х-у-5=0. Вектор является для искомой прямой направляющей. Воспользуемся (7) .

3у+6=-х+4, х+3у+2=0.

Ответ: х+3у+2=0.

Практическая работа

1. Задан треугольник АВС. Составить уравнения стороны АВ, медианы АМ и высоты АН.

2. Найдите угол между данными прямыми.

3. Установить соответствие.

4. Из перечисленных ниже уравнений прямых укажите прямую:

   • Параллельную оси Ох;

   • Параллельную оси Оу;

   • Проходящую через начало координат.

Вариант 1 А(2;3), B(-2;3), C(0;5). 3х+2у-1=0 и 5х-у+4=0. Пары прямых: Y - 5X - 8 = 0, Y - 5X + 8 = 0 пересекаются Y - 4X - 7 = 0, 4Y + X + 20 = 0 параллельны Y - 3X - 4 = 0, 3Y - 9X - 12 = 0 перпендикулярны Y - 6X -10 = 0, Y - 11X + 2 = 0 Совпадают а) у=-3х б) х=5 в) 2у-6=0
Вариант 2 А(2;-1), B(4;2), C(0;1). 3х-2у+0,1=0 и 2х+3у-5=0. Пары прямых: 2Y - 5X -8 = 0, 4Y -10X -10 = 0 пересекаются Y + 2X - 7 = 0, 2Y - X + 20 = 0 параллельны Y - 5X -10 = 0, Y - X + 10 = 0 перпендикулярны 3Y - 9X -12 = 0, 5Y -15X - 20 =0 совпадают а) у=33х б) 2х=-5 в) 2у-4=0
Вариант 3 А(1;0), B(5;7), C(4;5). х-2=0 и х-у+1=0. Пары прямых: 2Y - 6X - 8 = 0, 3Y - 9X -12 = 0 перпендикулярны 2Y + 8X - 7 = 0, 4Y - X + 20 = 0 совпадают Y - 6X -10 = 0, 3Y -11X + 2 = 0 пересекаются 2Y - 5X -18 = 0, 4Y -10X +18 = 0 параллельны а) х-5=0 б) 5у=-4 в) у=7х
Вариант 4 А(2;-1), B(-2;4), C(5;7). 3х-4у-8=0 и 8х+6у+5=0. Пары прямых: 2Y + 7X - 6 = 0, 4Y - X + 20 = 0 перпендикулярны 2Y - 3X - 8 = 0, 3Y – 4,5X -12 = 0 совпадают 3Y - 6X -10 = 0, 3Y -10X + 2 = 0 пересекаются 2Y - 5X -18 = 0, 6Y -15X +18 = 0 параллельны а) у=-9х б) х=-25 в) 2у-1=5
Вариант 5 А(-10;2), B(-4;1), C(6-3). 4х-3у+8=0 и 3х+4у-15=0. Пары прямых: Y + 4X - 7 = 0, Y - 8X + 20 = 0 перпендикулярны 2Y - 7X - 8 = 0, 3Y – 10,5X -12 = 0 совпадают Y - 4X -10 = 0, 3Y -12X -30 = 0 пересекаются 2Y - 5X -18 = 0, 5Y +2X +18 = 0 параллельны а) у=-3х б) х=-11 в) 2у+2=0
Вариант 6 А(12;1), B(5;-1), C(-4;5). 2х-5у-1=0 и 4х+3у+2=0. Пары прямых: -3Y + 8X - 17 = 0, 4Y - X + 2 = 0 перпендикулярны 2Y - 6X - 7 = 0, 5Y - 15X -12 = 0 совпадают Y - 6X -10 = 0, 4Y -24X -40 = 0 пересекаются 5Y - X -18 = 0, 4Y +20X +18 = 0 параллельны а) у-13=0 б) 4х=-11 в) у+2х=0
Вариант 7 А(2;-1), B(-3;4), C(5;7). 2х-3у+5=0 и 3х+2у-7=0. Пары прямых: 3Y + 4X - 7 = 0, 4Y - 3X + 20 = 0 перпендикулярны 2Y - 5X - 8 = 0, 3Y - 9X -12 = 0 совпадают Y - 7X -10 = 0, 3Y -21X + 2 = 0 пересекаются 2Y - 5X -18 = 0, 4Y -10X -36 = 0 параллельны а) 4у=3 б) 5х-11=0 в) у-5х=0
Вариант 8 А(-2;3), B(-5;7), C(-4;2). 2х-3у+10 и 5х-у+4=0. Пары прямых: -2Y + 5X - 7 = 0, 4Y - 3X + 2 = 0 перпендикулярны 2Y - 5X = 0, 3Y – 7,5X -2 = 0 совпадают Y - 4X -10 = 0, 2Y -8X - 20 = 0 пересекаются Y - 5X -18 = 0, Y +0,2X -36 = 0 параллельны а) -4у=3 б) 7х=-11 в) 4у-х=0
Вариант 9 А(2;5), B(-4;5), C(11;2). 3х+5у-7=0 и 2х-4у+5=0. Пары прямых : 8Y + 3X - 7 = 0, 4Y +1,5X + 20 = 0 перпендикулярны 2Y - 5X - 8 = 0, 5Y – 12,5X -20 = 0 совпадают Y - 7X -10 = 0, 3Y -21X + 21 = 0 пересекаются 2Y - 3X -18 = 0, 4Y -6X -36 = 0 параллельны 4. а) 5у-3=0 б) 7х=5 в) у-4х=0
Вариант 10 А(-2;5), B(-7;1), C(6;2). х-2у+5=0 и 3х-у+4=0. Пары прямых: 3Y - 4X +2 = 0, 4Y +3X + 20 = 0 перпендикулярны 2Y - 5X - 8 = 0, 8Y - 9X -12 = 0 совпадают 4Y - 7X -1 = 0, 8Y -14X - 2 = 0 пересекаются 2Y - 5X -18 = 0, 4Y -10X = 0 параллельны а) -6х=3 б) у=-5 в) у-х=0
Вариант 11 А(-3;5), B(7;5), C(7;0). х+у+3=0 и 2х+2у-1=0. Пары прямых: 3Y + X - 7 = 0, 4Y - 12X + 7 = 0 перпендикулярны 2Y - 6X - 8 = 0, 3Y - 9X -12 = 0 совпадают Y - 9X -10 = 0, 3Y -27X -30 = 0 пересекаются 2Y - X -18 = 0, 4Y -2X -36 = 0 параллельны а) 8у-3=0 б) 7х=5 в) 4у-х=0
Вариант 12 А(5;-1), B(2;3), C(4;1). 2х+3у+4=0 и х-5у+3=0. Пары прямых: -3Y + 4X - 7 = 0, 4Y + 3X = 0 перпендикулярны 10Y - 5X - 8 = 0, 2Y - X -12 = 0 совпадают Y - 8X -10 = 0, 4Y -32X -40 = 0 пересекаются 2Y - 9X -18 = 0, Y -10X -36 = 0 параллельны а) 8у+1=0 б) -7х=9 в) 4у=х
Вариант 13 А(7;1), B(-2;0), C(5;-1). 2х-4у+1=0 и 3х-у+2=0. Пары прямых: 3Y + 15X - 2 = 0, Y + 5X +2 = 0 перпендикулярны Y - 3X - 8 = 0, 2Y - 6X -16 = 0 совпадают Y - 2X +3 = 0, 4Y +2X -5 = 0 пересекаются 3Y - X -8 = 0, Y -X -3 = 0 параллельны а) -у+1=10 б) -7х=-2 в) 3у+х=0
Вариант 14 А(3;-2), B(2;5), C(-1;3). х-5у+4=0 и 3х-5у+6=0. Пары прямых: Y + 3X - 17 = 0, 2Y + 3X-2 = 0 перпендикулярны 4Y - 6X - 5 = 0, 6Y - 9X -2 = 0 совпадают Y - 2X +3 = 0, 4Y +2X -1 = 0 пересекаются 2Y - 9X -18 = 0, Y -18X -32 = 0 параллельны а) 5у-1=0 б) 3х+9=4 в) 4у-5х=0

Контрольные вопросы:

1. Дайте определение линии на плоскости.

2. Запишите уравнения прямых, параллельных осям координат.

3. Запишите в общем виде уравнение прямой, проходящей через начало координат.

4. Как выглядит уравнение прямой в отрезках? Общее уравнение?

5. Сформулируйте условие перпендикулярности прямых.

6. Сформулируйте условие параллельности прямых.

7. Как найти угол между прямыми?

Практическая работа №8

«Кривые второго порядка»

Цель работы: научится исследовать и строить кривые второго порядка.

Теоретическая часть

Линии, определяемые алгебраическими уравнениями второй степени относительно переменных х и у, уравнениями вида

, (1)

где А, В, С одновременно не равны нулю, называются кривыми второго порядка.

1. Окружность. Простейшей кривой второго порядка является окружность.

Окружностью называется множество точек на плоскости, удаленных от заданной точки A этой же плоскости на одно и тоже расстояние R>0. Точка А называется центром окружности, а d-радиусом окружности.

Общее уравнение окружности с центом А(х_0;у₀) и радиусом R имеет вид:

. (2)

Рис.1

В частности, если центр находится в т.О(0;0), то уравнение (1) примет вид:

2. Эллипс. Эллипсом называется множество всех точек плоскости, сумма расстояния от каждой из которых до двух данных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

каноническим уравнением эллипса:

, a>0, b>0 (3)

Если a>b, то a--большая полуось, b—малая полуось эллипса. Координаты фокусов

F₁(-c;0), F₂(c;0), c²=a²-b², . (см.рис.2)

Очевидно, для эллипса ε < 1.

Рассмотрим свойства эллипса.

Свойства эллипса:

• Эллипс пересекает каждую из осей координат в двух точках.

• Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

• Эллипс имеет две взаимно перпендикулярные оси симметрии.

• Эллипс имеет центр симметрии.

Эллипс может быть получен сжатием окружности, чем больше ε, тем более сжат эллипс.

При малых значениях эксцентриситета эллипс мало отличается от окружности. При ε = 0 эллипс превращается в окружность.

Прямая x = –d называется директрисой, соответствующей фокусу F₁(-c; 0). Наряду с этой директрисой вводят прямую x = d, которая является директрисой, соответствующей фокусу F₂(c; 0).

Если b>a то b--большая полуось, a—малая полуось эллипса. Координаты фокусов

F₁(0;c), F₂(0;-c), c²=b²-a², . (см.рис.3)

Рис.2 рис.3

3. Гипербола. Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Каноническое уравнение гиперболы: _, (4)

где а—действительная, а b—мнимая полуось гиперболы. , F₁(-c;0), F₂(c;0),

c²=a²+b². Число называется эксцентриситетом гиперболы. ε>1, т.к. с>a.

Асимптоты гиперболы определяются уравнениями: (См. рис.4)

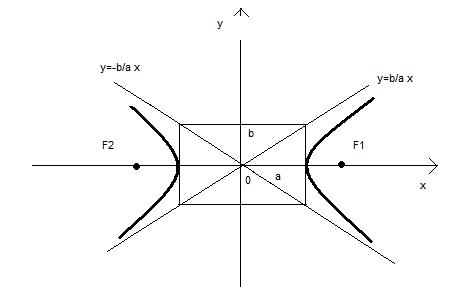
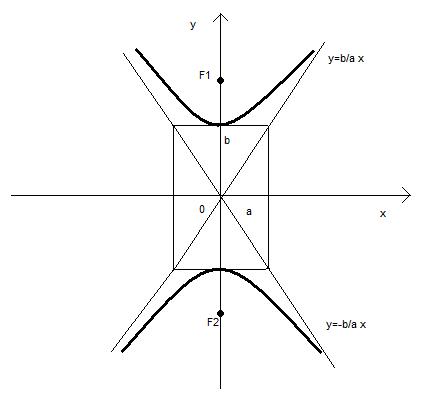
Рис.4 рис.5

 Если а = b, , то гипербола называется равнобочной (равносторонней)

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .

Гипербола может быть задана уравнением . В данном случае , F₁(0;c), F₂(0;-c), , асимптота определяется уравнением , а уравнение директрисы . (см. рис.5).

4. Парабола. Параболой называется множество всех точек плоскости, каждая из которых равноудалена от заданной точки этой же плоскости, называемой фокусом, и заданной прямой, называемой директрисой.

Каноническое уравнение параболы имеет два вида:

1) y² = 2рx - парабола симметрична относительно оси Оx. (см. рис.6)

2) y² = -2рx - парабола симметрична относительно оси Оx.

3) x² = 2рy - парабола симметрична относительно оси Оy.

4) x² = -2рy - парабола симметрична относительно оси Оy.

В обоих случаях р>0 и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат. р—это расстояние от фокуса F до директрисы l, называется параметром параболы.

Парабола, уравнение которой y ² = 2рx имеет фокус F( р/2,0) и директрису x = - р/2, фокальный радиус-вектор точки M(x,y) на ней r = x+ р/2.

Рис. 6

Парабола, уравнение которой x² =2рy имеет фокус F(0, р/2) и директрису y = - р/2; фокальный радиус-вектор точки M(x,y) параболы равен r = y + р/2.

Каноническое уравнение параболы имеет вид: ,

Где число p>0, Координаты фокуса . Точка О(0;0) называется вершиной параболы, длина r отрезка FM—фокальный радиус точки М, ось Ох—ось симметрии параболы.

 Данная прямая в канонической системе координат называется директрисой параболы. Расстояние от нее до фокуса называется фокальным параметром параболы. Очевидно, он равен p. Эксцентриситет параболы по определению полагают равным единице, то есть ε = k = 1.

Вид параболы в канонической системе координат и расположение ее директрисы приведены на рис.

Практическая часть

1. Пример 1. Найдите координаты центра и радиус окружности х²+у²-6х-12у+13=0.

Решение. Выделим в уравнении полные квадраты и приведем его к стандартному виду.

х²+у²-6х-12у-4=0.

,

Сопоставляя полученное уравнение с уравнением (2) можно сделать вывод: х₀=3, у₀=6, R=7.

Ответ: х₀=3, у₀=6, R=7.

Пример 2. Составить уравнение эллипса, фокусы которого лежат на оси Ох, ε=0,8 и 2а=10.

Решение. Т.к. фокусы эллипса лежат на оси Ох, 2а является большой осью и .

. Координаты фокусов F₁(-c;0), F₂(c;0), т.е. .

Подставляя в общее уравнение эллипса найденные значения параметров, получим искомое уравнение

Ответ:

Пример 3. Составить каноническое уравнение гиперболы, если расстояние между фокусами 26, а эксцентриситет .

Решение. Из условия 2с=26, следовательно, с=13. Т.к. , то очевидно, что а=12. Найдем малую полуось гиперболы

.

Уравнение гиперболы имеет вид:

Ответ: .

Пример 4. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением _.

Решение. Находим фокусное расстояние c² = 25 – 9 = 16. Для гиперболы: c² = a² + b² = 16,  ;  c = 2a; c² = 4a²;  a² = 4; b² = 16 – 4 = 12. Т.о.

 - искомое уравнение гиперболы.

Ответ: .

Пример 5. Составьте каноническое уравнение параболы и уравнение ее директрисы, фокус которой имеет координаты F(-4;0).

Решение. Т.к. фокус лежит на отрицательной полуоси Ох, то уравнение параболы имеет вид: y² = -2рx. По условию , 2p=16. Итак уравнение параболы имеет вид: у²=-16х. Уравнение директрисы х=4.

Ответ: у²=-16х, х=4.