Высшая категория - кубическая сингония

Необходимым условием отнесения кристаллов к кубической сингонии является присутствие четырех осей третьего порядка - 4L₃.

Элементарная ячейка кристаллов кубической сингонии имеет форму куба и обладает наивысшей симметрией (рис. 13). Координатные оси X, Y, Z располагаются под углом 90 друг к другу.

Параметры элементарной ячейки: a₀ =b₀=c₀; ===90

Рис. 13. Элементарная ячейка кристаллов кубической сингонии.

В кубической сингонии выделяется пять классов симметрии:

1. 3L₄ 4L₃ 6L₂ 9P C

2. 3L₄ 4L₃ 6L₂

3. 4L₃ 3L₂ 6P

4. 4L₃ 3L₂ 3P C

5. 4L₃ 3L₂

Для кристаллов кубической сингонии характерен изометрический (равновеликий) облик.

Среди простых форм кристаллов этой сингонии выделяются основные и производные. Свое название они получают по числу и форме граней (табл. 1, рис. 14).

Таблица 1.

Простые формы кристаллов кубической сингонии

№	Основные формы	Производные формы	Кол-во граней	Форма грани
1	Тетраэдр		4	Равносторонний треугольник
2		Тригонтритетраэдр	12	Равнобедренный треугольник
3		Тетрагонтритетраэдр	12	Четырехугольник
4		Пентагонтритетраэдр	12	Несимметричный пятиугольник
5		Тригонгексатетраэдр (гексатетраэдр)	24	Разносторонний треугольник
6	Октаэдр		8	Равносторонний треугольник
7		Тригонтриоктаэдр	24	Равнобедренный треугольник
8		Тетрагонтриоктаэдр	24	Четырехугольник
9		Пентагонтриоктаэдр	24	Несимметричный пятиугольник
10		Тригонгексаоктаэдр (гексаоктаэдр)	48	Разносторонний треугольник
11	Гексаэдр (куб)		6	Квадрат
12		Тригонтетрагексаэдр (пирамидальный куб)	24	Равнобедренный треугольник
13	Ромбо-додекаэдр		12	Ромб с углами наклона 45 к двум координатным осям и параллельный третьей
14	Пентагон-додекаэдр		12	Симметричный пятиугольник с углами наклона 30 и 60 к двум координатным осям и параллельный третьей
15		Дидодекаэдр	24	Четырехугольник

Ориентировка кристаллов при проектировании (рис. 15, 16).

С координатными осями XYZ совмещают 3L₄ (1 и 2 классы симметрии) (рис. 16а) или 3L₂ (3 - 5 классы симметрии) (рис. 16б).

Единичная грань - грань октаэдра или тетраэдра - отсекает равные единичные отрезки на координатных осях. Если единичная грань в кристалле отсутствует, то можно в качестве единичных выбрать отрезки любой одинаковой длины по X, Y, Z.

Возможные положения проекций граней простых форм и элементов симметрии кристаллов кубической сингонии приведены на рисунках 15, 16.

11

6

1

12

7

2

13

8

3

9

14

4

15

10

5

Рис. 14. Простые формы кристаллов кубической сингонии.

1. 3L₄ 4L₃ 6L₂ 9P C

3. 4L₃ 3L₂ 6P

5. 4L₃ 3L₂

2. 3L₄ 4L₃ 6L₂

4. 4L₃ 3L₂ 3P C

Рис. 15. Стереографические проекции элементов симметрии пяти классов кубической сингонии.

8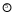

8

8

а

б

5

5

5

Рис. 16. Схема расположения проекций граней простых форм и осей симметрии кристаллов кубической сингонии.

а - 1 и 2 классы симметрии:

1 - куб; 2 - октаэдр; 3 - ромбододекаэдр;

4 - тригонтетрагексаэдр; 5 - тетрагонтриоктаэдр;

6 - тригонтриоктаэдр; 7 – тригонгексаоктаэдр, 8 - пентагонтриоктаэдр.

б - 3, 4, 5 классы симметрии:

1 - тетраэдр; 2 - тригонтритетраэдр;

3 - тетрагонтритетраэдр; 4 - тригонгексатетраэдр;

5 - пентагонтритетраэдр; 6 - пентагондодекаэдр.

РАБОТА 6