38

Лабораторна робота № 4 по дисципліні "Антені системи"

ОДЕСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ ЗВ'ЯЗКУ ім. О.С. ПОПОВА

Кафедра технічної електродинаміки та систем радіозв’язку

Дослідження множника системи дискретних антенних решіТок

методичні вказівки до використання лабораторної роботи №4

за дисципліною «Антені системи»

для студентів денної та заочної форми навчання за дисципліною професійної

підготовки бакалаврів за напрямом вищої освіти 6.050901 – Радіотехніка

Одеса 2012

УДК 621.392.67

Укладач Т.А. Цалієв

Рецензенти: зав. каф. ТЕД та СРЗ, проф. Проценко М.Б.,

доц. каф. ТЕД та СРЗ, доц. Драганов В.М.

Методичні вказівки до лабораторної роботи студентів по дисципліні «Антені системи» / Укл. Т.А. Цалієв. – Одеса: Вид-во ОНАЗ ім. О.С. Попова, 2012. – __ с.

Метою методичних вказівок є допомога студентам при самостійному вивченні теоретичних положень дисципліни «Антени та пристрої НВЧ», виконані індивідуальних завдань та лабораторних робот.

Методичні вказівки призначені для студентів денної та заочної форм навчання інституту радіоелектроніки.

Методичні вказівки розглянуті та затверджені на засіданні кафедри технічної електродинаміки та систем радіозв'язку

(протокол № ____ от « » ____________ 20 р.)

Дослідження множника системи дискретних антенних решіТоК

1. Мета роботи

Ціль даної роботи полягає в ознайомленні студентів з основами класифікації антенних решіток і застосовуваною термінологією, вивченні конструктивних і функціональних особливостей, методики розрахунків параметрів, наочної ілюстрації впливу геометричних параметрів антеною решітки, амплітудно-фазового розподілу збудливих струмів на її спрямовані властивості й інші характеристик.

Перелік розглянутих питань:

• класифікація антенних решіток;

• основна термінологія;

• теорема перемножування й поняття множника системи;

• властивості дискретної антенної решітки;

• вивчення впливу геометричних параметрів, амплітудно-фазового розподілу збудливих струмів антенної решітки на її спрямовані властивості.

2. Основи теорії антенних решіток

Одним зі способів досягнення необхідних високих спрямованих властивостей антен, є використання антенних решіток – багатоелементних систем, у яких елементи збуджуються струмами з необхідним співвідношенням амплітуд і фаз. У конструктивнім ставленні застосування таких решіток створює передумови для зменшення поздовжніх розмірів антен високого ступеня спрямованості й, як наслідок, зменшує займані ними об'єми.

Антенна решітка (АР) це антенна система, що складається з декількох однакових і однаково орієнтованих антенних елементів.

1. Класифікація антенних решіток і термінологія

Класифікація антенних решіток може здійснюватися різним способом:

По геометричних ознаках:

• лінійні (прямолінійні), кільцеві антенні решітки;

• плоскі, опуклі, конформні й об'ємні антенні ґрати;

• дискретні й безперервні антенні решітки;

• еквідистантні, не еквідистантні антенні решітки.

По способу збудження:

• рівно амплітудні, синфазні й не синфазні антенні решітки;

• антенні решітки з паралельною, послідовною й змішаною схемою живлення.

• комутаційні антенні решітки;

• фазованні антенні решітки;

• антенні решітки із синтезованим розкривом.

По типу елементів:

• вібраторні антенні решітки;

• хвилеводні антенні решітки;

• рупорні антенні решітки;

• решітки спіральних антен;

• решітки діелектричних стрижневих антен;

• хвилевідно-щілинні антенні решітки;

• мікросмужкові антенні решітки.

По спрямованих властивостях:

• антенні решітки нормального, похилого, осьового (зворотного осьового) випромінювання;

• багатопроменеві антенні решітки;

• сканувальні антенні решітки

• антенні решітки, що пере відбувають

• поза спрямовані антенні решітки;

Дискретною називають антенну решітку, що складається з кінцевого числа елементів.

Безперервною називають антенну решітку кінцевих розмірів, що містить нескінченне число елементів.

Лінійні антенні решітки утворені елементами, фазові центри яких розташовані на одній (не обов'язково прямой) лінії. У плоскій антеної решитці фазові центри елементів лежать в одній площині.

Еквідистантною називають антенну решітку, усі елементи якої розташовані на однаковій відстані друг від друга.

Конформні антенні решітки – це решітки, в якої випромінюча поверхня повторює форму поверхні деякого об'єкта.

У рівноамплітудної антеної решітці усі елементи збуджені струмами (полями) з однаковими амплітудами, у синфазних решітках фази збудливих струмів (полів) однакові.

Фазована антенна решітка (ФАР) являє собою систему антенних елементів з електричним керованням фазовим розподілом збудливих струмів (полів).

У сканувальної антеної решітці реалізована функція керування просторовим положенням головної пелюстки діаграми спрямованості – сканування.

Багатопроменевими звичайно називають фазовані антенні решітки, з кількома входами, кожному з яких відповідає незалежно керована головна пелюстка парціальної діаграми спрямованості. Амплітудно-фазове збудження елементів решітці формують за допомогою діаграмоутворюючою схеми (ДУС)

Адаптивні антенні решітка являє собою систему, що складається з антенної решітки і пов'язаного з нею пристрою обробки сигналу (процесора), що змінює свої параметри відповідно до інформації, укладеної в прийнятих сигналах.

Активної фазованної антенної решіткой (АФАР) називають систему, що містить у кожному елементі (залежно від її призначення) активний модуль: генератор, підсилювач, перетворювач або множник частоти.

Вісь решітці  уявлювана лінія, на якій розташовуються фазові центри її елементів.

Крок решітці  відстань між фазовими центрами сусідніх елементів.

Розкрив решітці  це ділянка уявлюваної поверхні, у межах якого розташовані випромінюючі поверхні всіх елементів розглянутої решітки.

Амплітудний розподіл  функція, що відображає послідовність значень амплітуд збудливих струмів (або полів), залежно від порядкового номера елемента решітки.

Фазовий розподіл  функція, що відображає послідовність значень фаз збудливих струмів (або полів), залежно від порядкового номера елемента решітки.

Коефіцієнт затримки  величина рівна відношенню фазової швидкості хвилі, що поширюється в напрямку яко какой-нибудь координати розкриву решітки до швидкості світла у вільному просторі.

Множник системи антеної решитці  це комплексна характеристика спрямованості уявлюваного аналога даної решітки, утвореного з ненаправлених елементів.

2. Найпростіші розрахункові співвідношення

Якщо знехтувати взаємним впливом елементів, то з достатнім ступенем точності характеристика спрямованості антеної решітки може бути представлена у вигляді добутку характеристики спрямованості елемента такої системи, на множник системи (множник комбінування). Це співвідношення називають теоремою перемножування :

, (2.1)

де – характеристика спрямованості одиночного елемента решітки, а функція зветься множником системи.

При розв'язку задачі дослідження властивостей антеною решітки в строгій постановці слід ураховувати взаємний вплив сусідніх елементів, яке може бути різним (скажемо, у центральній частині, на краю решітки), внаслідок чого властивості (повний вхідний опір, ДС, розподіл струмів) елементів решітки виявляються неоднаковими.

Із практичної точки зору найбільш наочним є вивчення спрямованих властивостей антенних решіток на прикладі лінійної эквидистантной решітки.

При заданих геометричних параметрах решітки характер випромінювання визначається амплітудним і фазовим розподілом струмів (полів) у її елементах.

Розрізняють три режими роботи лінійної антеної решітки при лінійному законі розподілу фаз: режим нормального випромінювання (де різниця фаз струмів (полів) у сусідніх елементах ), режим похилого випромінювання ( ) і режим осьового випромінювання ( ).

Множник системи эквидистантной равноамплитудной антеної решітки при лінійному набігу фази описується виразом

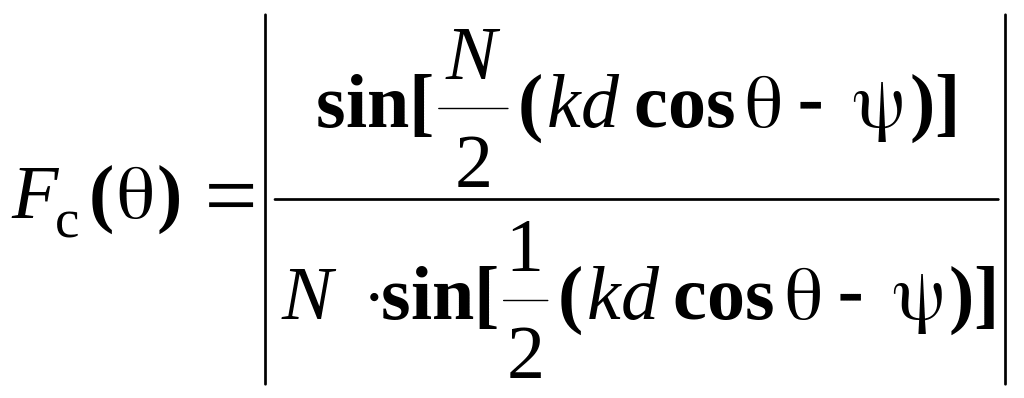, (2.2)

де – число елементів у решітці, – крок решітки, кут відлічується від осі ґрат, , – довжина хвилі у вільному просторі.

Режим нормального випромінювання ( ). Аналізуючи вираз (2.2) можна визначити напрямки, у яких випромінювання відсутнє (нулі характеристики спрямованості). Дорівнюючи чисельник в (2.2) нулеві знайдемо

, , (2.3)

де знак «плюс» відповідає напрямкам , а знак «мінус» – . З (2.3) одержуємо формулу, що визначає положення нулів амплітудної характеристики спрямованості

Ширину головної пелюстки ДС за рівнем нульового випромінювання й за рівнем половинної потужності можна визначити, скориставшись виразами

, .

Функціональна залежність множника системи від координатного кута, обумовлена виразом (2.2), є періодичною з періодом рівним .

Відзначимо, що при великому кроці решітки спостерігається поява побічних головних пелюсток, між якими завжди є нулів і бічних пелюсток, зменшення кроку веде до зменшення числа побічних головних максимумів.

Для того, щоб повністю виключити появу в множнику системи декількох головних пелюсток, слід вибирати крок решітки виходячи з умови , а для зменшення рівня бічних пелюсток рекомендується застосовувати ще більш жорсткий критерій: . При цьому для таких решіток рівень першої бічної пелюстки дБ.

Коефіцієнт спрямованої дії рівно амплітудної лінійної решітки у режимі нормального випромінювання при числі елементів і кроці можна розрахувати по наступній наближеній формулі

,

де  довжина решітки.

Коефіцієнт спрямованої дії рівно амплітудної лінійної решітки у режимі осьового випромінювання ( при й кроці ) можна розрахувати по наступній наближеній формулі:

.

Оптимальний режим осьового випромінювання відповідає (при обраній кількості елементів і кроці решітки при ) максимуму КСД. При цьому оптимальне значення фазового зсуву струмів (полів) у сусідніх елементах визначається зі співвідношення

.

Коефіцієнт спрямованої дії решітки в оптимальному режимі

.

Режим похилого випромінювання ( ). У цьому випадку всі елементи рівно амплітудної решітки збуджуються з постійним фазовим зсувом, причому фаза збудливого струму лінійно наростає (або убуває) з зростанням номера елемента. Максимум випромінювання відхиляється від осі решітки, при цьому для окремих елементів різниця ходу хвиль у цьому напрямку компенсується зсувом фази збудливого струму , звідки маємо .

З останнього виразу видне, що, змінюючи фазовий зсув, можна керувати кутовим положенням головного максимуму ДС решітки. Напрямки нульового випромінювання ДС визначаються з умови , з якого випливає . При відносно малих відхиленнях ширина головної пелюстки ДС визначається по формулах

, .

Режим осьового випромінювання ( ). При синфазне додавання полів здійснюється в напрямку осі решітки , у цьому режимі для одержання тільки одного головного максимуму крок решітки слід вибирати значно меншим чим .

При напрямків, у яких поля всіх елементів синфазні, не існує. Однак, при значеннях фазового зсуву близьких до , основна пелюстка ДС звужується тем сильніше, чим більше , а відносний рівень бічних пелюсток при цьому зростає.

Обидва перераховані фактори по-різному впливають на величину максимального КСД. А саме: на початку, у міру зростання переважає фактор звуження головної пелюстки ДС і КСД зростає, досягаючи максимуму при . Потім КСД починає падати через зростання відносного рівня бічних пелюсток ДС.

Оптимальний режим осьового випромінювання відповідає ( при обраній кількості елементів, кроці решітки і ) максимумові КНД.

При цьому оптимальне значення фазового зсуву струмів (полів) у сусідніх елементах визначається зі співвідношення ; ширина головної пелюстки ДН може бути знайдена з виразів , ; а відносна розмір першої бічної пелюстки ДС дБ.