Вычисление количества связных компонент
Полостями
множества 
называются
связные компоненты множества 
.
На гексагональной решетке количество
связных компонент 
и
количество полостей 
множества
связаны
соотношением
,
(10.18)
где
символом 
обозначено
количество конфигураций 
,
встречающихся в множестве
.
Доказательство этого утверждения можно
найти в [10.2, р.185]. Если компоненты
не
содержат полостей, то
просто
равно их количеству, поскольку в этом
случае
состоит
из одной связной компоненты и,
следовательно, 
.
Но, подсчета связных компонент как мы
видели раньше, НМ-преобразование выделяет
в исходном множестве точки, окрестность
которых совпадает со структурным
элементом. Используя в НМ-преобразовании
структурные элементы, приведенные на
рис. 10.16, получим
(10.19)
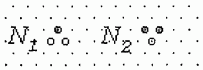
Рис.10.16. Структурные элементы, используемые для подсчета связанных компонент(точкой обозначено начало)
Утончение и утолщение
Операция утончения (thinning) определяется как
,
(10.20)
а операция утолщения (thickenning) — как
(10.21)
где 
—
структурный элемент, состоящий из двух
непересекающихся подмножеств
и 
.
Отметим,
что если начало структурною элемента
принадлежит
,
то 
,
если же начало принадлежит
,
то 
.
Поэтому в первом случае 
при
любом
,
а во втором —
при
любом
.
Чтобы избежать получения этих тривиальных
результатов, всегда будем полагать, что
при выполнении операции утончения
(соответственно, утолщения) начало
структурного элемента не
принадлежит
(соответственно,
).
Кроме того, можно показать, что 
,
где 
.
Примеры операций утончения и утолщения
приведены на рис.10.17.
Так
же как и ранее, введем последовательность
структурных элементов 
и
обозначим
(10.22)
последовательные утончения и
(10.22')
последовательные утолщения множества с помощью последовательности структурных элементов .
Рис.
10.17. Утончение и утолщение: а - серыми
кружками помечено исходное множество;
б - черными кружками помечен результат
HM-преобразования посредством структурного
элемента 
,
а крестиками - результат HM-преобразования
посредством структурного элемента
(начало
структурного элемента - кружок с точкой
в центре); в — утончение;
г — утолщение
Изучим
результат последовательных утончений
множествa
посредством
последовательности структурных
элементов 
,
где 
отличаются
друг от друга поворотом вокруг центральной
точки (рис. 10.18). На крайнем правом рисунке
показан установившийся результат
последовательных утончений, который
при последующих утончениях не изменяется.
Рис. 10.18. Последовательные утончения
Приведенный пример демонстрирует применение операции утончения для построения скелетона (или скелета) множества . Понятие скелетона (или скелета) достаточно интуитивно. На этом уровне его иногда пытаются описать с помощью качественной модели «степного пожара». Представим себе степной массив, покрытый сухой травой. Допустим, что одновременно вдоль всей границы массива вспыхивает огонь, распространяющийся во всех направлениях с одинаковой скоростью. В первый момент фронт распространения огня совпадает с границей. По мере его распространения различные участки фронта встречаются друг с другом и в местах встречи фронтов огонь будет гаснуть. Вот эти места самогашения огня и образуют "скелетон" массива (рис. 10.19).
Для непрерывного двумерного пространства в работе [10.2] сформулированы следующие свойства точек скелетона множества :
-
если точка 
является
точкой скелетона, и 
—
наибольший круг с центром в точке
,
содержащийся в
,
то невозможно найти содержащийся
в
больший
круг (не обязательно с центром в точке
),
содержащий
;
- круг касается границы множества в двух или более точках.
Там
же дано одно из определений скелетона:
скелетон 
множества
есть
множество центров максимальных кругов,
содержащихся в
.
Под максимальным кругом подразумевается
круг, касающийся границ множества
в
двух или более точках. Рис. 10.20 иллюстрирует
это определение.
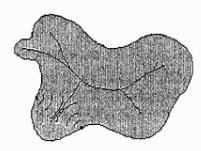
Рис. 10.19. Формирование линии гашения огня
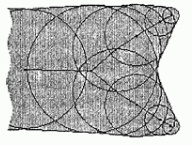
Рис. 10.20. К определению скелетона. Максимальные круги
Из этого определения (и из рис. 10.20) следует одно замечательное свойство скелетона: если каждой точке скелетона сопоставить значение радиуса максимального круга, центром которого она является, то по скелетону можно восстановить множество , его породившее:
,
где 
-
радиус максимального круга для точки
-
скелетона, 
-
круг единичного радиуса. Отметим без
доказательства еще одно важное свойство
скелетона: если множество
связно,
то его скелетон
тоже
является связным множеством.
К сожалению, скелетон множества, заданного на дискретной решетке, только приближенно напоминает скелетон непрерывного множества. Более того, для одного и того же множества результат построения скелетона посредством последовательных утончений может быть различным в зависимости от порядка структурных элементов в последовательности (топологические свойства скелетона, такие как количество связных компонент, точек разветвления, ветвей, концевых точек и тому подобное при этом сохраняются). Это снова связано с анизотропией дискретного пространства. Тем не менее применение дискретного скелетона иногда оказывается чрезвычайно полезным. Так, скелетонизацию часто используют при обработке чертежей или распознавании символов для сведения линий к единичной ширине. Построение скелетона фоновой компоненты изображения, содержащего некоторое множество объектов, позволяет сегментировать его на участки, каждый из которых можно интерпретировать как зону влияния (жизненное пространство) объекта. Статистический анализ размеров, ориентации и количества соседей таких зон применяется при анализе прочностных характеристик материалов, при исследовании поведения популяций микроорганизмов и развития лесных массивов. Множество примеров применения операций утончения, утолщения и построенной на них скелетонизации можно найти в [10.2, 10.4].
102. Алгоритмы сжатия без потерь.
Алгоритм RLE
Первый вариант алгоритма
Данный алгоритм необычайно прост в реализации. Групповое кодирование — от английского Run Length Encoding (RLE) — один из самых старых и самых простых алгоритмов архивации графики. Изображение в нем (как и в нескольких алгоритмах, описанных ниже) вытягивается в цепочку байт по строкам растра. Само сжатие в RLE происходит за счет того, что в исходном изображении встречаются цепочки одинаковых байт. Замена их на пары <счетчик повторений, значение> уменьшает избыточность данных.
Алгоритм декомпрессии при этом выглядит так:
Initialization(...); do { byte = ImageFile.ReadNextByte(); if(является счетчиком(byte)) { counter = Low6bits(byte)+1; value = ImageFile.ReadNextByte(); for(i=1 to counter) DecompressedFile.WriteByte(value) } else { DecompressedFile.WriteByte(byte) } while(ImageFile.EOF());
В данном алгоритме признаком счетчика (counter) служат единицы в двух верхних битах считанного файла:
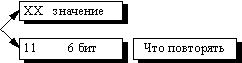
Соответственно оставшиеся 6 бит расходуются на счетчик, который может принимать значения от 1 до 64. Строку из 64 повторяющихся байтов мы превращаем в два байта, т.е. сожмем в 32 раза.
Упражнение: Составьте алгоритм компрессии для первого варианта алгоритма RLE.
Алгоритм рассчитан на деловую графику — изображения с большими областями повторяющегося цвета. Ситуация, когда файл увеличивается, для этого простого алгоритма не так уж редка. Ее можно легко получить, применяя групповое кодирование к обработанным цветным фотографиям. Для того, чтобы увеличить изображение в два раза, его надо применить к изображению, в котором значения всех пикселов больше двоичного 11000000 и подряд попарно не повторяются.
Вопрос для самоконтроля: Предложите два-три примера “плохих” изображений для алгоритма RLE. Объясните, почему размер сжатого файла больше размера исходного файла.
Данный алгоритм реализован в формате PCX. См. пример в приложении.