Теоремы по алгебре и геометрии 1 курс 1 семестр

Геометрния

Окружность.

Окружность радиуса R с центром в точке M0(x0, y0) имеет уравнение

Доказательство. Пусть M(x,y) -- текущая точка окружности. По определению окружности расстояние MM0 равно R:

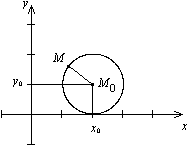
По формуле скалярного произведения для плоскости получаем, что точки окружности и только они удовлетворяют уравнению

Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение.

Если в уравнении (12.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (12.2). Для этого достаточно выделить полные квадраты по переменным X и Y.

Эллипс.

Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами – 2c . Тогда в выбранной системе координат эллипс имеет уравнение

Доказательство. Пусть M(x,y) -- текущая точка эллипса. По определению эллипса F1M+F2M=2a . Из треугольника F1MF2 (рис. 12.3) видно, что F1M+F2M > F1F2 , то есть 2a>2c, a>c, и поэтому число b=sqrt(a^2 - b&2) существует.

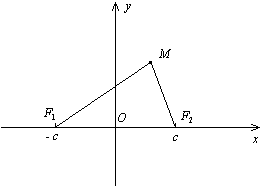
Фокусами в выбранной системе координат являются точки F1(-c,0) , F2(c,0). По формуле (10.4) для плоского случая находим

Тогда по определению эллипса

Пренесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что b^2= a^2 - c^2, имеем равенство

Наконец, разделив обе части на (a^2)(b^2) , получим исходное уравнение (12.4).

Гипербола.

Пусть расстояние между фокусами F1 и F2 гиперболы равно 2c , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a . Тогда гипербола в выбранной выше системе координат имеет уравнение

Доказательство. Пусть M(x,y) -- текущая точка гиперболы (рис. 12.9).

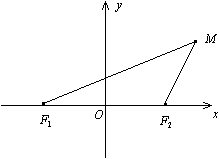
Так как разность двух сторон треугольника меньше третьей стороны, то |F1M – F2M| < F1F2 , то есть 2a<2c , a<c . В силу последнего неравенства вещественное число b , определяемое формулой (12.9), существует.

По условию, фокусы – F1(-c,0) , F2(c,o) . По формуле (10.4) для случая плоскости получаем

По определению гиперболы

Это уравнение запишем в виде

Обе части возведем в квадрат:

После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные члены, получим

С учетом формулы (12.9) уравнение принимает вид

Разделим обе части уравнения на (a^2)(b^2) и получим исходное уравнение (12.8)

Парабола.

Пусть расстояние между фокусом F и директрисой l параболы равно P . Тогда в выбранной системе координат парабола имеет уравнение

Доказательство. В выбранной системе координат фокусом параболы служит точка F(p/2,0) , а директриса имеет уравнение x=-p/2 (рис. 12.15).

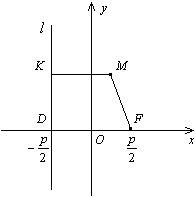
Пусть M(x,y) -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим

Расстоянием от точки M до директрисы l служит длина перпендикуляра MK , опущенного на директрису из точки M . Из рисунка 12.15 очевидно, что MK=x+p/2 . Тогда по определению параболы MK=FM , то есть

Возведем обе части последнего уравнения в квадрат:

Откуда

После приведения подобных членов получим исходное уравнение (12.10).

Расстояние от точки до плоскости. Расстояние от точки до прямой(вычисляется по нижепривиденной формуле отбрасыванием координаты z).

Пусть плоскость П задана уравнением Ax+By+Cz+D=0 и дана точка M0(x0,y0,z0) . Тогда расстояние p от точки M0 до плоскости П определяется по формуле

Доказательство. Расстояние от точки M0 до плоскости П -- это, по определению, длина перпендикуляра M0K , опущенного из точки M0 на плоскость П (рис. 11.9).

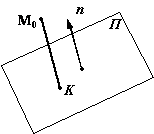
Вектор KM0 и нормальный вектор n плоскости П параллельны, то есть угол альфа между ними равен 0 или пи , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

Координаты точки К , которые нам неизвестны, обозначим x1,y1,z1 . Тогда вектор KM0 = (x0-x1, y0-y1, z0-z1) . Так как n=(A,B,C) , то n*(вектор)KM0 = A(x0-x1) + B(y0-y1) + C(z0-z1) . Раскрыв скобки и перегруппировав слагаемые, получим

Точка K лежит на плоскости П , поэтому ее координаты удовлетворяют уравнению плоскости: Ax1+By1+Cz1+D=0 . Отсюда находим, что Ax1+By1+Cz1=-D . Подставив полученный результат в формулу (11.9), получим n*(vector)KM0=Ax0+By0+Cz0+D . Так как |n|=koren(A^2+B^2+C^2) , то из формулы (11.8) следует формула (11.7).

Угол между двумя прямым на плоскости.

Пусть заданы две прямые y = k2*x+b2 и y = k1*x+b1 , ( k2>k1). Тогда, если k1*k2!=-1 , то угол fi между этими прямыми можно найти из формулы

Если k1*k2=-1 , то прямые перпендикулярны

Доказательство. Как известно из школьного курса математики, угловой коэффициент в уравнении прямой y=kx+b равен тангенсу угла alfa наклона прямой к оси Ox . Из рис. 11.10 видно, что fi=alfa2-alfa1 .

Так как tg(alfa1)=k1 , tg(alfa2)=k2 , то при k2*k1!=-1 выполняется равенство

что и дает исходную формулу.

Если же k1*k2=-1, то tg(alfa1)*tg(alfa2)=-1, откуда

Следовательно

Каноническое уравнение прямой в пространстве.

Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой

Пусть для прямой Y известны ее направляющий вектор p=(k,l,m) и точка M0(x0,y0,z0) , лежащая на этой прямой. Пусть M(x,y,z) -- произвольная (текущая) точка прямой Y . Обозначим через r0 и r радиус-векторы точек M0 и M соответственно (рис. 11.11).

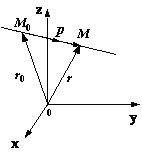
Тогда вектор M0M коллинеарен вектору p и, следовательно, M0M=tp , где t -- некоторое число. Из рис. 11.11 видно, что

r = r0 + tp

Это уравнение называется векторным уравнением прямой или уравнением в векторной форме.

От векторного соотношения перейдем к соотношениям координат. Так как (x,y,z) -- координаты точки M , то r=(x,y,z) , r0=(x0,y0,z0) , tp=(tk,tl,tm) . Из формулы (11.12) получим

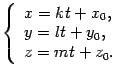
Полученная система уравнений называется параметрическими уравнениями прямой.

Выразим параметр t:

Так как во всех трех соотношениях параметр t имеет одно и то же значение, то

Эти уравнения называются каноническими1 уравнениями прямой.

Линейка

Правило Крамера: Если в системе n линейных уравнений с n неизвестными delta !=0 , то система имеет решение и притом единственное. Это решение задается формулами

где A(ij) -- алгебраические дополнения. Тогда из (15.3) следует, что

Заметим, что по формуле (14.13) разложение определителя delta1 по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя delta2 по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому:

откуда и следует утверждение данной теормеы.

Теорема Кронекера-Капелли

Система линейных уравнений (15.1) является совместной тогда и только тогда, когда ранг матрицы системы A равен рангу расширенной матрицы A* .

Доказательство. Оно распадается на два этапа.

1. Пусть система имеет решение. Покажем, что RgA=RgA*

.

Пусть набор чисел (a1,a2,,..,an) является решением системы. Обозначим через a(i) i -ый столбец матрицы A , i=1,2…n . Тогда a1a1+ a2a2+…+anan=b, то есть столбец свободных членов является линейной комбинацией столбцов матрицы A . Пусть r=RgA . Предположим, что RgA*!=RgA . Тогда по предложению 15.1 RgA*=r+1 . Выберем в A* базисный минор M . Он имеет порядок r+1 . Столбец b свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы A . Столбец свободных членов в миноре M является линейной комбинацией столбцов матрицы A . В силу свойств определителя ( предложения 14.13, 14.18) M=a1M1+a2M2+…+anMn , где M(i) -- определитель, который получается из минора M заменой столбца свободных членов на столбец a(i) . Если столбец a(i) проходил через минор M , то в M(i) , будет два одинаковых столбца и, следовательно,M(i)=0 . Если столбец a(i) не проходил через минор M , то M(i) будет отличаться от минора порядка r+1 матрицы A только порядком столбцов. Так как RgA=r , то M(i)=0 . Таким образом,M=a1*0+a2*0+…+an*0=0 , что противоречит определению базисного минора. Значит, предположение, что RgA*!=RgA , неверно.

2. Пусть RgA=RgA* . Покажем, что система имеет решение. Так как RgA=RgA* , то базисный минор M матрицы A является базисным минором матрицы A* . Пусть через минор M проходят столбцы a(i1),a(i2),…,a(ir) . Тогда по теореме о базисном миноре в матрице A* столбец свободных членов является линейной комбинацией указанных столбцов:

Положим x{i1}=a1 , x{i2}=a2,…, x{ir}=ar ,остальные неизвестные возьмем равными нулю. Тогда при этих значениях получим

В силу равенства (15.6) x{1}a{1}+x{2}a{2}+…+x{n}a{n}=b . Последнее равенство означает, что набор чисел x1,x2,…,xn является решением системы. Существование решения доказано.

При элементарных преобразованиях ранг матрицы не меняется

Доказательство. Пусть ранг матрицы A равен r , A’ -- матрица, получившаяся в результате выполнения элементарного преобразования.

Рассмотрим перестановку строк. Пусть M -- минор матрицы A , тогда в матрице A’ есть минор M’ , который или совпадает с M , или отличается от него перестановкой строк. И наоборот, любому минору N’ матрицы A’ можно сопоставить минор матрицы A или совпадающий с N’ , или отличающийся от него порядком строк. Поэтому из того, что в матрице A все миноры порядка r+1 равны нулю, следует, что в матрице A’ тоже все миноры этого порядка равны нулю. И так как в матрице A есть минор порядка r , отличный от нуля, то и в матрице A’ тоже есть минор порядка r , отличный от нуля, то есть RgA’=r .

Рассмотрим умножение строки на число a , отличное от нуля. Минору M из матрицы A соответствует минор M’ из матрицы A’ или совпадающий с M , или отличающийся от него только одной строкой, которая получается из строки минора M умножением на число, отличное от нуля. В последнем случае M’=aM . Во всех случаях или M и M’ одновременно равны нулю, или одновременно отличны от нуля. Следовательно, RgA’=r .

Пусть к i-ой строке матрицы A прибавлена ее j-ая строка, умноженная на число lamda . Рассмотрим миноры порядка r+1 в матрице A’ . Если через минор M’ не проходит i-ая строка, то он совпадает с минором M , расположенным в тех же строках и столбцах в матрице A , и следовательно, равен нулю.

Если через минор M’ проходят и i-ая и j-ая строки, то он получается из минора M , расположенного в тех же строках и столбцах матрицы A , прибавлением к i-ой строке минора M j-ой строки, умноженной на lamda . По свойству определителя M=M’ . Следовательно, M’=0 .

Пусть через минор M’ проходит i-ая строка и не проходит j-ая. Тогда M’ отличается от M i-ой строкой. Эта строка в M’ является строкой M , к которой добавлены элементы j-ой строки, умноженные на lamda . По свойствам определителей M’=M+lamda(+-N) , где N -- минор порядка r+1 матрицы A , стоящий в j-ой строке и в тех же строках, что и минор M , исключая i-ую, а знак " +-" связан с возможным изменением порядка строк. Так как все миноры порядка r+1 в матрице A равны нулю, то M’=0 .

Итак, в матрице A’ все миноры порядка r+1 равны нулю. Следовательно, RgA’<=r , то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что RgA’=k , и k<r . Тогда в матрице A’ к i-ой строке прибавим j-ую строку, умноженную на число (-lamba) . В результате получим исходную матрицу A . По только что доказанному RgA<=k<r . Получили противоречие: r<r . Предположение не верно, следовательно, RgA’=r .

Существование обратной матрицы.

Если матрица A имеет обратную, то |A|!=0 и |A^-1| = |A|^-1

Доказательство Так как определитель произведения матриц равен произведению определителей ( предложение 14.7), то . |A*A^-1| = |A|*|A^-1|=|E| . Так как определитель единичной матрицы равен 1 т.е. |E|=1 , поэтому |A|*|A^-1| =1, что невозможно при |A|=0 . Из предыдущего равенства следует также |A|=|A^-1. Следовательно, Если определитель матрицы равен нулю, то обратная к ней не существует.

Разложение определителя по произвольной строке.

Для определителя матрицы A справедлива формула

Доказательство. Если i=1 , положим B=A . Пусть i!=1 . Тогда i-ую строку поменяем местами со строкой с номером i-1 . Определитель сменит знак. Затем строку с номером i-1 поменяем местами со строкой с номером i-2 . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока i-ая строка матрицы A не станет первой строкой новой матрицы, которую мы обозначим B . Отметим, что в матрице B , начиная со второй строки, стоят строки матрицы A , причем порядок их следования не изменился.

При переходе от матрицы A к матрице B определитель сменит знак i-1 раз. Таким образом

Это соотношение верно и при . По определению 14.6 определителя,

где N{k} -- определитель матрицы, полученной из матрицы B вычеркиванием первой строки и k-ого столбца. Первая строка матрицы B совпадает с i-ой строкой матрицы A , поэтому b{1k}=a{ik} . Результат вычеркивания в матрице B первой строки и k-ого столбца будет таким же, как при вычеркивании в матрице A i-ой строки и k-ого столбца. Поэтому N{k}=M{ik} , где M{ik} -- определитель матрицы, полученной при вычеркивании в матрице A i-ой строки и k-ого столбца. Следовательно,

следовательно

По определению 14.7 алгебраического дополнения получим

Тогда из предыдущего равенства вытекает

Что и требовалось доказать.

Вектора.

Предложение 10.6 Система векторов A1,…..,Ak линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

Доказательство. Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов j1,j2,..jk , что j1*A1 + j2*A”+…jk*Ak=0 , причем хотя бы один коэффициент отличен от нуля. Предположим, что A1 !=0 . Тогда

то есть A1 является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор A1 , то есть A1 = v2*A2+v3*A3+…+vk*Ak . Очевидно, что –A1+v2A2+…+vkAk=0 . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен -1 ).

Следующее предложение показывает геометрический смысл смешанного произведения.

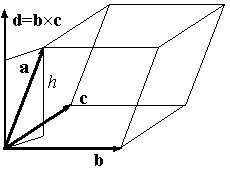
Предложение 10.27 Смешанное произведение abc некомпланарных векторов равно объему параллелепипеда, сторонами которого служат векторы a,b,c, взятому со знаком " + ", если векторы образуют правую тройку, и со знаком " - ", если -- левую.

Доказательство. Пусть d = b x c . По предложению 10.22 |d| равен площади S параллелограмма, сторонами которого служат векторы b,c (рис. 10.26, 10.27).

По свойству 7 скалярного произведения ( теорема 10.2)

Пусть h -- высота параллелепипеда (рис. 10.26, 10.27). Если a,b,c -- правая тройка векторов, то Пр a(на d) =h (рис. 10.26),

Если a,b,c -- левая тройка, то Пр а(на d) = -h . Так как S*h=V -- объем параллелепипеда, то из формулы (10.7) получим

Abc=V в случае правой тройки и abc= -V в случае левой тройки сомножителей.

Заметим, что если тройка векторов a,b,c является правой, то тройки c,a,b и b,c,a также будут правыми, а тройки b,a,c, c,b,a и a,c,b будут левыми тройками векторов.

Так как объем параллелепипеда не зависит от того, в каком порядке перечисляются его стороны, то

Представление векторного произведения через координаты векторов.

Пусть a = (A1,A2,A3), b = (B1,B2,B3) . Тогда

Доказательство. По условию a = A1*i+A2*j+A3*k , b = B1*i+B2*j+B3*k . В силу предложений 10.20 и 10.21 получим

По тем же правилам

По таблице умножения i x b = B2*k – B3*j . Аналогично находим j x b = -B1*k + B3*i , k x b = B1*j – B2*i . Подставив полученные результаты в формулу (10.5), получим

Представление скалярного произведения через координаты векторов.

Если векторы в ортонормированном базисе заданы своими координатами a = (A1,A2,A3) , b = (B1,B2,B3) , то

Доказательство. По условию a = A1*i+A2*j+A3*k , b = B1*i+B2*j+B3*k . В силу свойств 1 - 3 ( теорема 10.2) скалярного произведения получим

Используя те же свойства, находим a*i = (A1*i+A2*j+A3*k)*i = A1*i^2+A2*j*i+A3*k*i . В силу свойства 5, находим i^2=1 , а по свойству 8 получим j*i=k*i =0 . Таким образом, a*i=A1 . Аналогично находим, что a*j=A2 , a*k=A3 . Подставив полученные результаты в формулу

Получим исходную формулу.

Предложение 10.25 Если в правом ортонормированном базисе i,j,k заданы координаты векторов a = (A1,A2,A3) , b = (B1,B2,B3) , то

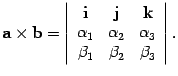
Доказательство. Достаточно лишь написать формулу вычисления приведенного в теореме определителя и сравнить ее с формулой

Смешанное произведение.

Предложение 10.30 Пусть в правом ортонормированном базисе i,j,k заданы векторы a = (A1,A2,A3) , b = (B1,B2,B3) , c = (Y1,Y2,Y3) . Тогда

Доказательство. По предложению 10.25 находим координаты вектора b x c :

По теореме 10.3 находим скалярное произведение вектора a на вектор b x c :

Правая часть этого неравенсва совпадает с определением определителя

По определению a*b*c = a*(b x c)

Что и требовалось доказать.

Свойство дистрибутивности скалярного произведения.

a(b+c)=ab+ac;

Докажем/ В силу свойства 7:

Если a !=0

имеем a(b+c) = |a|*Пр(b+c) на a. Т.к. Пр(b+c) на a=Пр b на a + Пр c на a. Поэтому

Если же а =0 то св-во очевидно.

Распределительное свойство векторного произведения.

Векторное произведение обладает свойством дистрибутивности, то есть a x (b+c)= a x b + a x c.

Доказательство. Выберем в пространстве правый ортонормированный базис i,j,k. Пусть d = a x (b+c)

d = (A,B,Y), d1=a x b, d1=(A1,B1,Y1), d2 = a x c, d2 = (A2,B2,Y2). Нам нужно доказать, что d = d1 + d2 , то есть что

выполняются равенства: A = A1 + A2, B = B1 + B2.

Т.к. Проекции вектора на координатные оси равны коодинатам вектора, то

По свойству линейности смешанного произведения

Аналогично доказываются равенства B = B1 + B2, Y = Y1 + Y2.