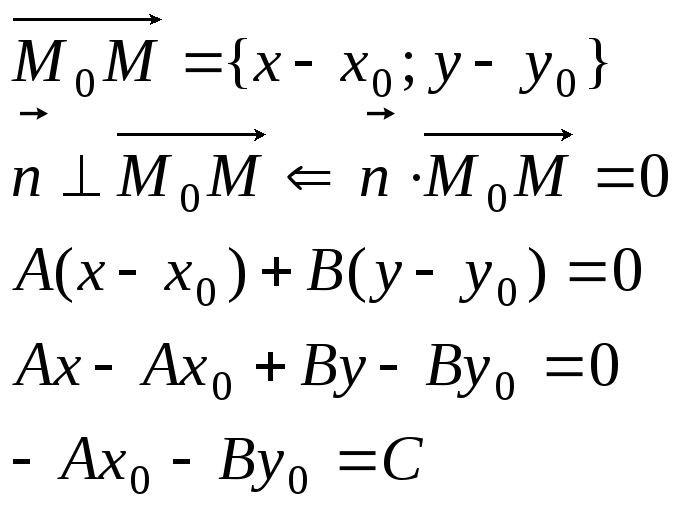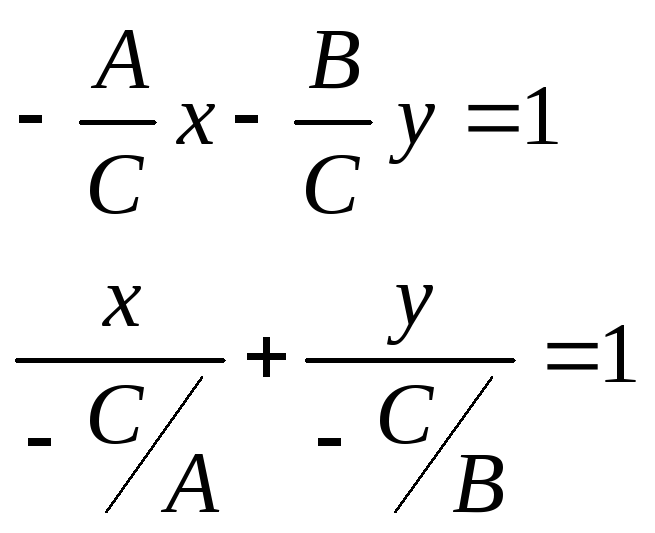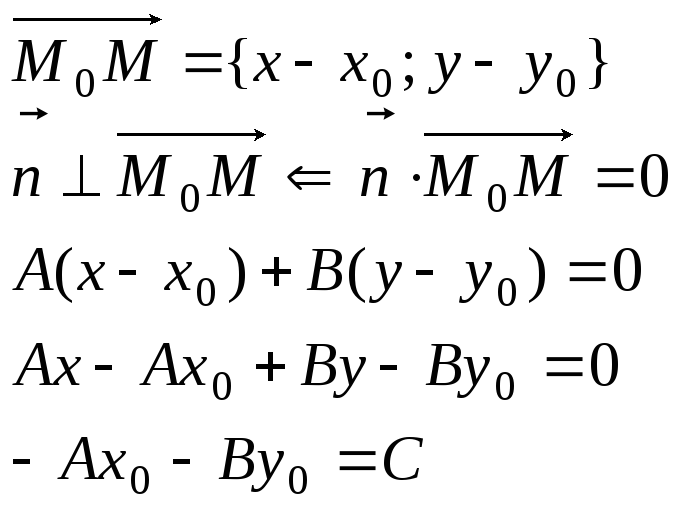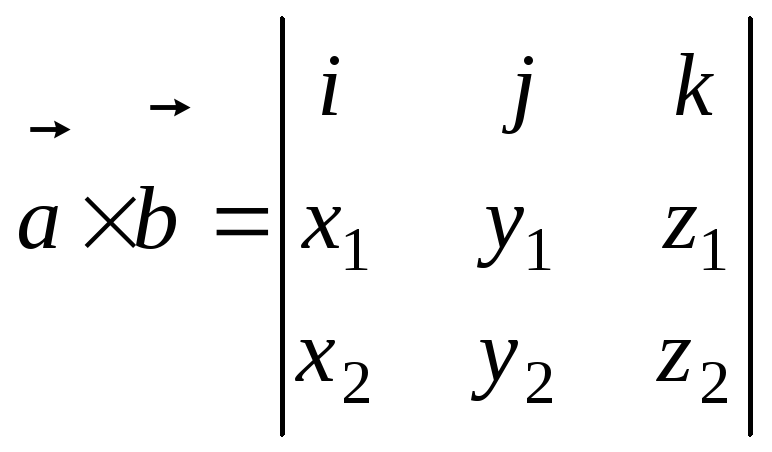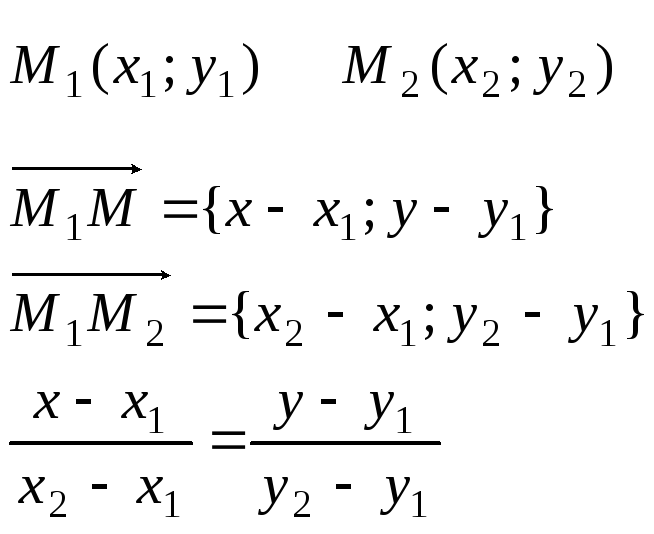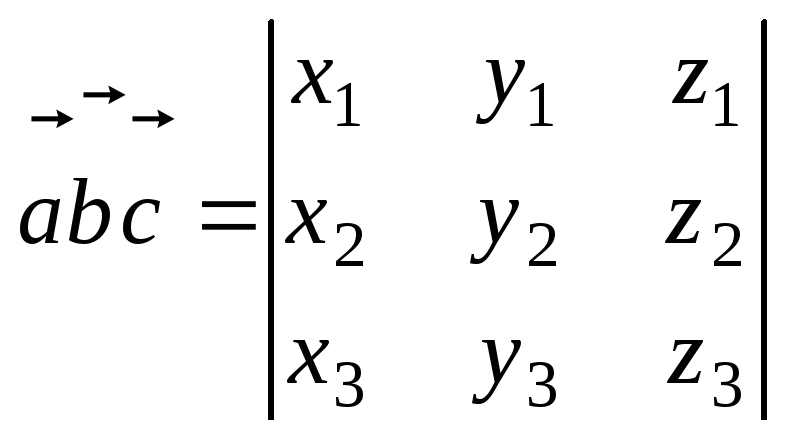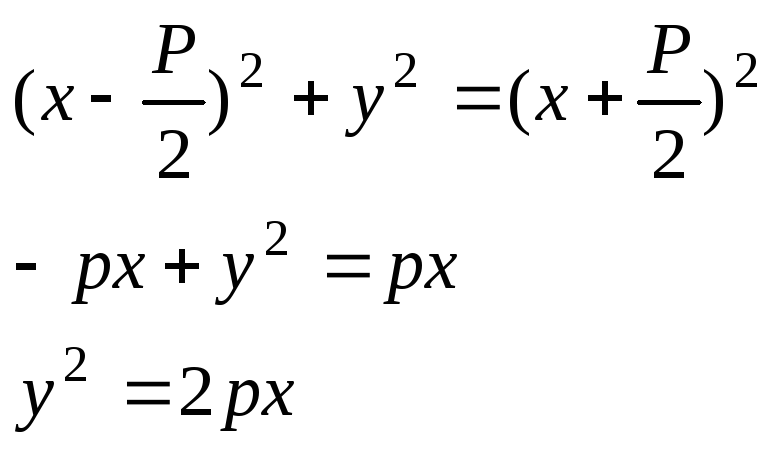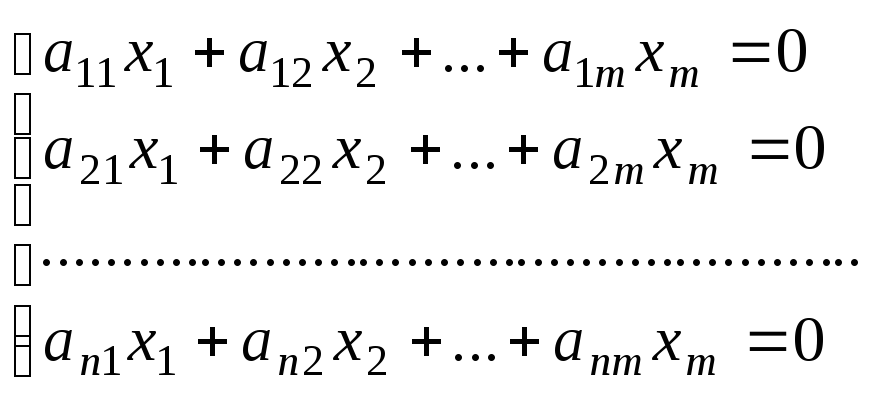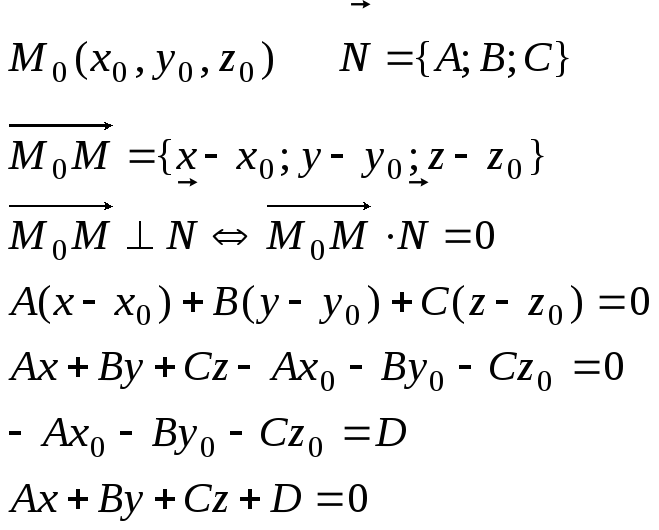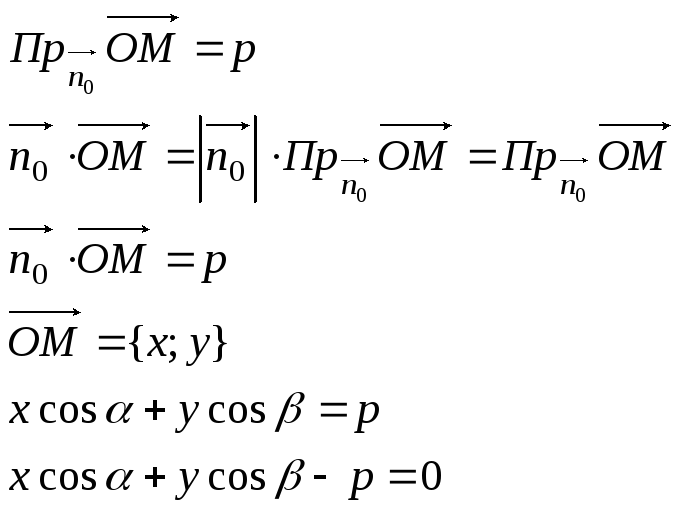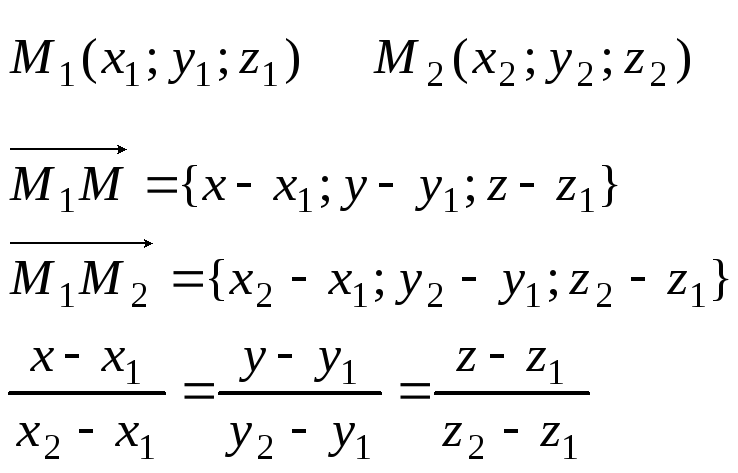шпора к колоше

Понятие о матрицах. Свойства определителей 3 порядка.

Числовой матрицей размерности m*n называется прямоугольная таблица, составленная из чисел, расположенных в m строках и n столбцах.

Определителем матрицы называется алгебраическая сумма всевозможных произведений, взятых по одному из каждой строки и каждого столбца со знаком «+» или «-».

Свойства определителя:

1. При транспонировании матрицы определитель не изменяется

2. При перестановке двух строк матрицы определитель меняет свой знак

3. Если к элементам какой-то строки прибавить элементы какой-то другой строки, умноженные на какое-либо число, то значение определителя не изменится

4. Если какая-то строка состоит из нулей, то определитель равен нулю

5. Если в определителе есть 2 пропорциональные строки, то определитель равен нулю

6. Если элементы какой-то строки имеют общий множитель, то его можно вынести за знак определителя.

Эллипсоид. Каноническое уравнение эллипсоида.

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

Однополостный гиперболоид. Каноническое уравнение однополостного гиперболоида.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

Двуполостный гиперболоид. Каноническое уравнение двуполостного гиперболоида.

Матрицы и действия над ними.

Матрица называется квадратной, если количество строк совпадает с количеством столбцов.

Если все элементы диагональной матрицы равны 1, то такая матрица называется единичной.

Матрица В называется обратной для матрицы А, если произведение А на В дает единичную матрицу.

Действия над матрицами:

1. Умножение матрицы на число

2. Матрицы одинаковой размерности можно складывать

3. Матрицы одинаковой размерности можно умножать

Гипербола. Каноническое уравнение гиперболы.

Геометрическое место точек, разность расстояний которых до двух данных точек есть величина постоянная, называется гиперболой.

Скалярное произведение и его свойства. Скалярное произведение в координатах

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Свойства скалярного произведения:

1. Коммутативность:

2. Дистрибутивность:

3. Скалярный множитель можно вынести за знак скалярного произведения:

Скалярное произведение в координатах:

Уравнение прямой в отрезках.

- общее уравнение прямой

- уравнение прямой в отрезках

Понятие вектора. Действия над векторами в геометрической форме.

Вектор – это направленный отрезок.

Пусть вектор обозначен или . Тогда длиной называется длина отрезка АВ.

Векторы называются коллинеарными, если они лежат на одной или на параллельных прямых.

Векторы равны, если они одинаково направлены и их длины равны.

Действия над векторами:

1. Суммой двух векторов называется вектор, полученный по следующей схеме (правило треугольника)

2. Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору

3. Умножение вектора на число

Понятие ранг матрицы. Свойства ранга матрицы.

Рангом матрицы называется наивысший порядок отличного от нуля минора.

Способ нахождения ранга матрицы: если нам удалось найти минор какого-то порядка, отличный от нуля, то затем мы составляем все возможные окаймляющие миноры. Если все они равны нулю, то и все другие миноры также будут равны нулю. Тогда ранг матрицы будет совпадать с порядком минора, который мы окаймили.

Если ранг матрицы (r) больше количества неизвестных (n), то системы несовместна и решений нет

Если r=n, то существует единственное решение

Если r<n, то существует бесконечное число решений

Свойства ранга:

1. При транспонировании матрицы ранг не меняется

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится

3. Ранг матрицы не изменяется при элементарных преобразованиях

Общее уравнение прямой на плоскости.

Параболоид. Каноническое уравнение параболоида.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

- эллиптический параболоид

-гиперболический параболоид

Сфера. Уравнение сферы в пространстве.

Сферой называется множество точек пространства, равноудаленных от данной точки на заданное положительное расстояние.

Векторное произведение и его свойства. Векторное произведение в координатах.

Векторным произведением вектора на вектор называется вектор , обозначаемый символом или и определяемый следующими условиями:

1.

2. ,

3. С конца вектора кратчайший поворот от к виден против часовой стрелки

Свойства Векторного произведения:

1. Векторное произведение антикоммутативно:

и противоположно направлены

2. Векторное произведение дистрибу-тивно:

3. Постоянный множитель можно вынести за знак векторного произведения:

при

при то же самое

Векторное произведение через координаты:

Умножение вектора на число. Теорема о разложении вектора по двум неколлинеарным.

Произведением вектора на число является вектор, обозначаемый , у которого направление совпадает с направлением если ; противоположно если , равен 0 при

Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам.

Д-во: докажем, что любой вектор можно разложить по двум данным неколлинеарным векторам и . Возможны 2 случая:

1) коллинеарен одному из данных векторов (например, ). Тогда по лемме о коллинеарных векторах , т.е. вектор разложен

2) неколлинеарен ни одному из данных векторов. Отметим какую-нибудь точку О и отложим от нее векторы , , . Через т. P проведем прямую, параллельную ОВ, и обозначим за А₁ точку пересечения этой прямой с прямой ОА. По правилу треугольника . Но векторы и коллинеарны соответственно векторам и , поэтому существуют такие числа x и y, что , . Следовательно,

Умножение вектора на число. Теорема о разложении вектора по трем некомпланарным.

Произведением вектора на число является вектор, обозначаемый , у которого направление совпадает с направлением если ; противоположно если , равен 0 при

Векторы называются компланарными, если они лежат в одной или параллельных плоскостях.

Теорема: Любой вектор в пространстве может быть представлен в виде линейной комбинации трех некомпланарных.

Д-во: -плоскость, в кот. лежат и

, причем и не равны 0 одновременно

лежит в одной плоскости с и

Существуют такие и , одновременно не равные 0, такие что ,

где ,

Составить уравнение прямой, проходящей через 2 данные точки.

Конус второго порядка.

Конусом называются поверхность, которые в некоторой системе декартовых прямоугольных координат определяется уравнением

Теорема Кронекера-Капелли.

Если ранг матрицы равен рангу расширенной матрицы, то систем имеет решения. В противном случае система решений не имеет.

Д-во: Пусть система совместна ранг расширенной матрицы равен рангу системы.

1) дополнительный столбец является линейной комбинацией системы. Это значит, что он не влияет на ранг по свойству ранга и это значит, что ранг расширенной матрицы равен рангу системы

2) пусть ранг расширенной матрицы равен рангу системы Выделим базисные столбцы расширенной матрицы, они же будут базисными столбцами матрицы системы. Предположим что базисными являются первые r столбцов Согласно теореме о базисном миноре (всякий столбец матрицы есть линейная комбинация ее базисных столбцов) последний столбец может быть линейной комбинацией базисных столбцов, вектор столбец”- решение системы значит система разрешима.

Ранг не может быть больше числа столбцов: если ранг расширенной матрицы равен числу столбцов то у системы одно решение, если ранг меньше числа столбцов то у системы множество решений.

Взаимное расположение плоскостей в пространстве.

1. Плоскости параллельны

и

2. Плоскости взаимно перпендикулярны

3. Между плоскостями угол, отличный от 0 и от 90, тогда угол между векторами и совпадает с одним из углов между этими плоскостями

Смешанное произведение и его свойства. Смешанное произведение в координатах.

Смешанным произведением трех векторов , , называется число, равное вектор-ному произведению , умноженному скалярно на вектор .

Свойства векторного произведения:

1. Смешанное произведение ассоциативно

2. Если векторы компланарные, то их смешанное произведение равно 0.

плоскости векторов , ; но тоже лежит в этой плоскости и

3.

Смешанное произведение в координатах:

Парабола. Каноническое уравнение параболы.

По определению параболы имеем:

Однородные системы уравнений.

Внешний вид однородной системы:

Такая система всегда имеет решения, т.к. расширенная матрица отличается от матрицы нулевым столбцом, который можно отбросить. Она всегда имеет тривиальные решения, но система обязательно будет иметь ненулевые решения.

Общее уравнение плоскости.

Нормальное уравнение прямой.

p – расстояние от прямой до (0;0)

Каноническое уравнение прямой в пространстве.

Уравнение прямой, проходящей через две точки в пространстве.