1.5.4. Метод деформируемого симплекса (метод Нелдера – Мида).

Метод деформируемого симплекса обладает большей общностью и позволяет учитывать локальные свойства поверхности целевой функции. Симплексы вытягиваются в направлении наклона поверхности, их оси поворачиваются при встрече с оврагом на поверхности целевой функции, вблизи минимума они сжимаются.

В рассматриваемом методе симплекс перемещается с помощью трех основных операций над симплексом: отражение, растяжение и сжатие.

Схема алгоритма.

Шаг 1.

Построение начального симплекса.

Задаются начальная точка х₀(0) и длина ребраl.Формируются остальные вершины симплекса:x_i(0)=x₀(0)+le_i (i=1,2,…,n), гдеe_i– единичные векторы.

Шаг 2.

Определение направления улучшения решения.

Для этого на каждой итерации вычисляются значения целевой функции в каждой вершине симплекса. Пусть для всех i

f(x_min(k))f(x_i(k)) f(x_m(k)) f(x_max(k)),

где min, m, max, i-номера соответствующих вершин симплекса. Определим центр тяжести всех точек, исключая точкуx_max(k),

Тогда направление улучшения решения определяется векторов

C_k- x_max(k).

Шаг 3.

Построение нового симплекса.

Замена вершины x_max(k) с максимальным значениемцелевой функции на новую точку с помощью операции отражения, результат которой является новая точка

u_k=C_k+*(C_k-x_max(k)), где -коэффициент отражения.

Шаг 4.

Построение нового симплекса.

Вычисляем f(u_k), при этом возможно один из трех случаев:

а) f(u_k)< f(x_min(k));

б) f(u_k)>f(x_m(k));

в) f(x_min(k))f(u_k) f(x_m(k));

Случай а): отражённая точка является точкой с наилучшим значением целевой функции. Поэтому направление отражение является перспективным и можно попытаться растянуть симплекс в этом направлении. Для этого строиться точка

V_k=C_k+*(u_k-C_k), где>1–коэффициент расширения.

Если f(v_k)<f(u_k), то вершинаx_max(k) заменяетсянаv_k, в противном случае наu_k и k-ая итерация заканчивается.

Случай б): в результате отражения получается новая точка u_k, которая, если заменитьx_max(k),сама станет наихудшей. Поэтому в этом случае производится сжатие симплекса. Для этого строится точкаv_k:

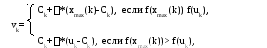
где 0<<1 –коэффициент сжатия.

Если f(v_k)<min{f(x_max(k)),f(u_k)}, то вершинаx_max(k) заменяется наv_k .

В противном случае вершинам x_i(k+1) (i=0,1,2,..,n)присваивается значение:

и на этом k-ая итерация заканчивается.

в) вершина x_max(k)заменяется наu_k, чем определяется набор вершин k+1-й итерации иk –ая итерация заканчивается.

Шаг 5.

Проверка сходимости.

Если

то поиск минимума заканчивается и полагается

Впротивном случае к=к+1 и происходит переход к шагу 2.

Опыт использования описанного алгоритма показывает, что целесообразно брать следующие значения параметров:

=1, =2,=0.5.

2.Задание на лабораторную работу.

1. Изучить изложенные методы многомерной безусловной оптимизации.

2. В соответствие с вариантом задания, определенным преподавателем, составить программы реализующие методы многомерной безусловной минимизации и найти точку минимума целевой функции f(x)=f(x⁽¹⁾, x⁽²⁾) с заданной точностью  указанными методами. Начальное приближение x₀ и точность  приводятся в условие задачи. Сравнить результаты, полученные разными методами для одной и той же целевой функции (в частности, сравнить число вычислении целевой функции и её производных, понадобившихся для получения заданной точности). Для каждого применяемого метода построить траекторию промежуточных точек, получаемых на очередных шагах метода исходящихся к точке минимума.

3. Оформить отчет о выполнении задания с приведением условия задачи, алгоритмов и программ указанных в задании методов минимизации, графиков траекторий промежуточных приближений, таблицы результатов сравнения рассмотренных методов, заключения по результатам сравнения методов.