Кольца Ньютона

Кольца Ньютона являются частным случаем интерференции в тонких пленках.

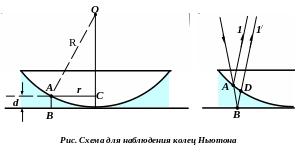
Схема для наблюдения колец Ньютона представлена на рис.. Роль тонкой пленки переменной толщины d выполняет воздушный клин, образованный плоскопараллельной пластиной и соприкасающейся с ней плосковыпуклой линзой большого радиуса кривизны R. Рассмотрим пучок параллельных лучей, падающий сверху на линзу. В точке А луч частично отразится, частично пройдёт в воздушный клин и отразится в точке В от пластинки.

Так как лучи 1 и 1^/ образовались из одного луча, то они являются когерентными и при наложении интерферируют. Линза имеет большой радиус кривизны, поэтому AВ  ВD  d. Оптическая разность хода этих лучей равна:

. (1)

В этом выражении:

• d - толщина зазора между пластиной и линзой,

• n - показатель преломления среды в зазоре (для воздуха n = 1),

• λ - длина волны падающего света,

• с лагаемое 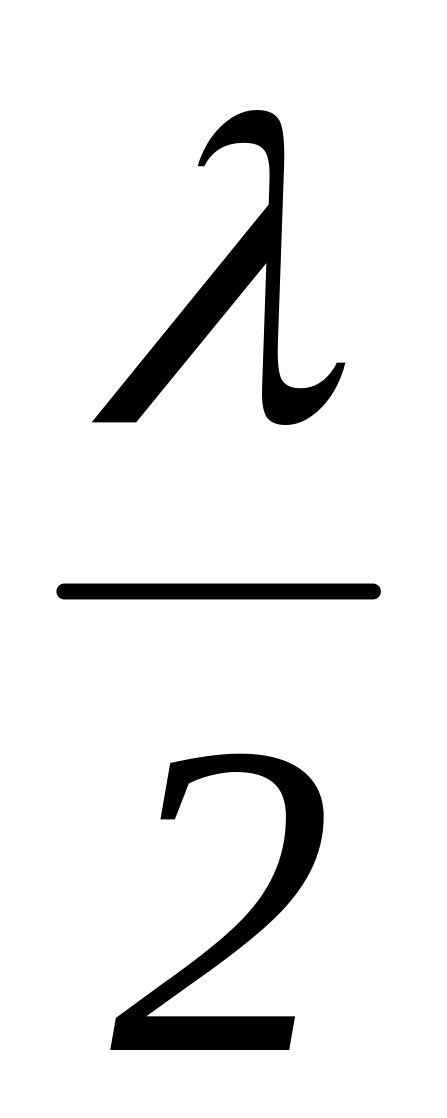учитывает изменение фазы световой волны на при её отражении от оптически более плотной среды (в точке В).

Так как геометрическим местом точек одинаковой толщины является окружность, то при освещении системы монохроматическим светом интерференционные полосы будут иметь вид тёмных и светлых колец с центром в точке соприкосновения линзы с пластиной (рис.2). Вблизи точки соприкосновения линзы и пластинки имеет место их деформация, поэтому в центре картины наблюдается круглое пятно.

Появление светлого или тёмного кольца зависит от того, чётное или нечётное число длин полуволн укладывается в оптической разности хода . Выражение для радиусов тёмных и светлых колец получим из условий минимумов и максимумов:

min или ; (2)

max или . (3)

Tолщина зазора между пластиной и линзой d зависит от радиуса кольца и радиуса кривизны линзы . Из треугольника ОАС следует:

, или . (4)

Слагаемое , и им можно пренебречь. Тогда и

. (5)

Подставим (5) в условия (2) и (3), получим выражения для радиусов тёмных и светлых колец в отраженном свете:

, (6)

, (7)

Удобно проводить измерения не радиусов, а диаметров D_к колец. Для диаметра тёмных колец получим:

(8)

Формула (8) не учитывает деформацию линзы и пластинки. Учёт деформации позволяет получить выражение:

. (9)

Здесь - диаметр центрального тёмного пятна (при k = 0).

Зависимость квадрата диаметра кольца от его порядкового номера представляет собой прямую линию. Отсекаемый на оси ординат отрезок позволяет найти , а угловой коэффициент этой прямой – радиус кривизны линзы. При выполнении лабораторной работы среднее значение радиуса кривизны линзы находится по формуле:

, (10)

где k > 0.