3.2. Выбор дробных реплик

При выборе функций отклика предполагалось, что известные коэффициенты при взаимодействиях факторов равны нулю, что далеко не всегда соответствует реальным ситуациям. Если применять регулярные реплики, то в этом случае возможны события, когда число неизвестных параметров функции отклика будет больше числа опытов {Y_u}.

В этом случае допускается оценивание коэффициентов при линейных членах, смешанных со взаимодействиями высших порядков. Может быть смешанной часть оценок при парных взаимодействиях.

Рассмотрим пример использования реплик для случая, когда число неизвестных параметров функции отклика больше числа опытов.

Пусть функция отклика имеет вид

=₀ + ₁x₁ +₂x₂ + ₃x₃ + ₁₂x₁x₂ +₁₃x₁x₃ + ₂₃x₂x₃. (3.2)

Имеется дробный факторный план D, задаваемый генерирующим соотношением х₃=х₁х₂:

.

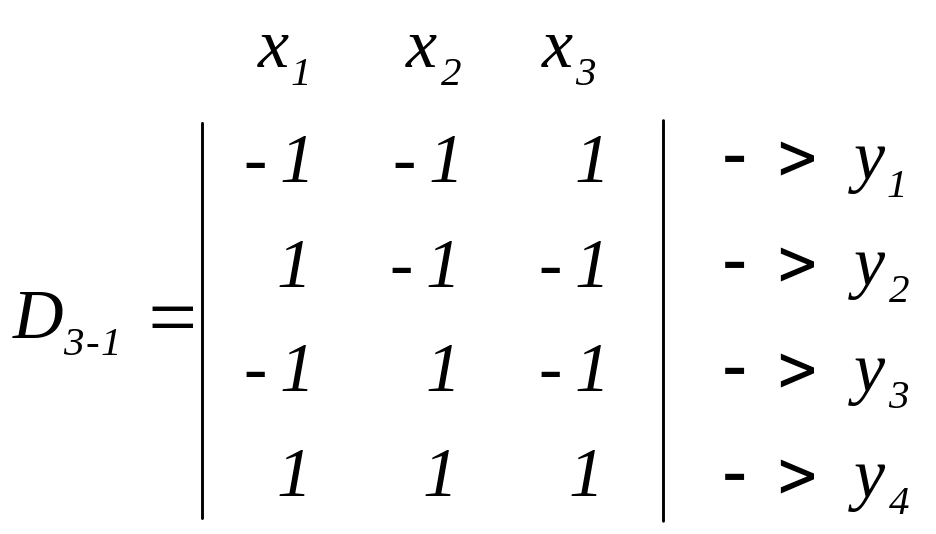Число неизвестных коэффициентов в функции отклика p+1=7, число наблюдений N₀=4, N₀<p+1.

Составим матрицу независимых переменных

Информационная матрица S=X^TX будет вырожденной, т к. она матрица порядка 7×7, а rankS=4. Следовательно, уравнение для определения оценок параметров функции отклика (1.7) будет иметь бесконечное множество решений.

Для рассмотренного примера модель наблюдений M{Y}=X, D{Y}=²₁I_n0 является моделью наблюдений неполного ранга, поскольку rankX=N₀<p+14. Здесь ²  неизвестный параметр, I_n0  единичная матрица порядка N₀.

Для получения решений сводят задачу исследований модели наблюдений неполного ранга к задаче исследования модели наблюдений полного ранга M{Y}=X⁰^r, D{Y}=²₁I_n, где X⁰=(X_ij),  матрица порядка r; ^r=⁰+A*, ^r=(₁,₂,…,_r)^T ‑ вектор неизвестных параметров;

A=(X^0TX)^-1X^0TX*,⁰=(₁,₂,…,_r)^T, *=(_r+1,_r+2,…,_p)^T, X=(X⁰,X*).

Свести модель наблюдений неполного ранга к модели наблюдений полного ранга можно, если допустить смешивание неизвестных параметров векторов ⁰ и *.

Как видно из матриц D_3-1 и X, в точках плана, в которых выполняются наблюдения {Y_u}, имеют место следующие равенства:

x₁=x₂x₃, x₂=x₁x₃, x₃=x₁x₂.

Функцию отклика (3.2) запишем в виде

(3.3)

^r₀=₀, ^r₁=₁+₂₃, ^r₂=₂+₁₃, ^r₃=₃+₁₂.

Эта функция отклика будет определена в точках плана D_3-1, а матрица X⁰ будет иметь вид

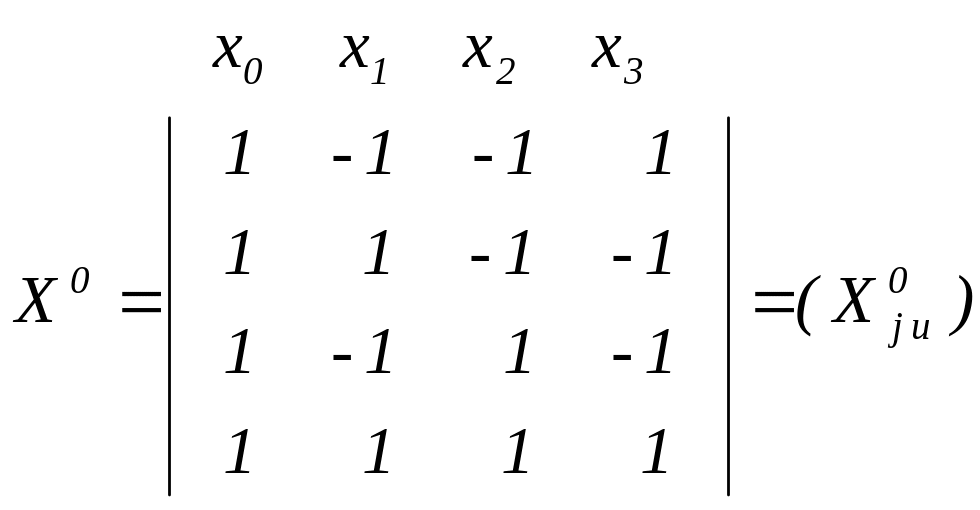
Функция отклика (3.3) соответствует модели наблюдений полного ранга, которая называется приведенной моделью

M{Y}=X⁰^r, D{Y}=²I₄, rankX⁰=rankX=4.

Матрица X⁰ является матрицей ортогонального планирования, следовательно, существуют однозначные оценки вектора ^r

^r=(X^0TX⁰)^-1X^0TY=(X^0TY)/N,

или для каждой j-ой компоненты

.

Отметим, что

.

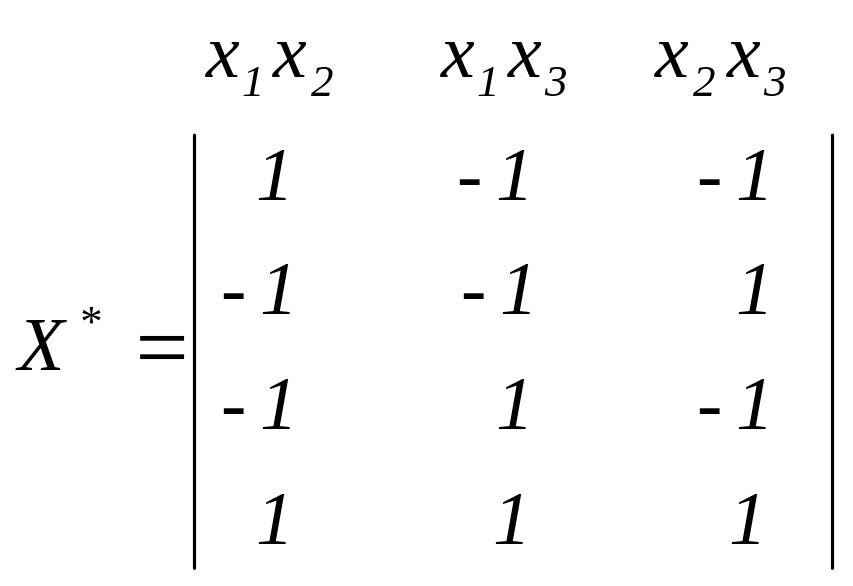Формально определено, что ^r=⁰+A*, причем ^r=(^r₀,^r₁,^r₂,^r₃)^T, ⁰=(₀,₁,₂,₃)^T, *=(₁₂,₁₃,₂₃)^T,

а матрицу A находим из уравнения A=(X^0TX)^-1X^0TX* и она имеет вид

.

Если решить при этих условиях уравнение ^r=⁰+A*, то получим систему параметрических функций

^r₀=₀, ^r₁=₁ + ₂₃, ^r₂= ₂ +₁₃, ^r₃=₃ + ₁₂.

Для получения правила смешивания, с помощью которого можно было определить, совокупность каких линейных эффектов и эффектов взаимодействия оценивается, введено понятие контраста плана или определяющего контраста. Правила смешивания с помощью определяющего контраста отображаются в системе линейно независимых параметрических функций, допускающих посмещенное оценивание.

Определяющим контрастом полуреплики 2^k-1 называют ее генерирующее соотношение, умноженное на свою левую часть [13].

Если генерирующее соотношение полуреплик 2^k-1 задано соотношением , где 1<i₁<i₂<…<i_m<k-1, 1<m<k-2, то, умножив его на x_k, получим .

Так как x_k[-1,+1], то определяющий контраст имеет вид

.

Умножая данные уравнения последовательно на переменные , получим систему равенств, на базе которой составляется система параметрических функций.

Например, для дробной реплики 2^3-1, задаваемой генерирующим соотношением х₃=х₁х₂, определяющий контраст имеет вид 1=x₁x₂x₃.

Умножим его на переменные х₁, х₂ и х₃ и получим систему равенств:

, , .

Эта система равенств устанавливает соответствие для составления системы параметрических функций

^r₁=₁ + ₂₃ <===> x₁=x₂x₃;

^r₂= ₂ +₁₃ <===> x₂=x₁x₃;

^r₃=₃ + ₁₂ <===> x₃=x₁x₂.

Но данный подход не позволяет получить несмещенные (раздельные) оценки параметров ₁, ₂, ₃. Чтобы решить эту задачу, достаточно построить еще полуреплику 2^3-1, которая будет задаваться генерирующим соотношением х₂=-х₁х₃. Система равенств, отображающих смешивание, будет иметь вид

x₁=-x₂x₃; x₂=-x₁x₃; x₃=-x₁x₂.

Следовательно, возможно МНК-оценка следующих неизвестных коэффициентов:

^r*₁=₁+₂₃, ^r*₂=₂+₁₃, ^r*₃=₃+₁₂.

На основе оценок полуреплик 2^3-1 (х₄=х₁x₃) и 2^3-1 (х₄=-х₁x₃) находим несмещенные оценки

.

Рассмотрим аналогичную задачу нахождения смещенных оценок для полуреплики 2^4-1.

Пусть функция отклика имеет вид

.

Матрица плана ДФЭ 2^4-1 построена с использованием генерирующего соотношения х₄=х₁х₂. Определяющий контраст имеет вид

1=x₁x₂x₄.

Умножим его последовательно на переменные х₁, х₂, х₃, х₄. Получим следующую систему равенств:

1=x₁x₂x₄; x₁=x₂x₄; x₂=x₁x₄; x₃=x₁x₂x₃x₄; x₄=x₁x₂; x₁x₃=x₂x₃x₄; x₂x₃=x₁x₃x₄; x₃x₄=x₁x₂x₃.

Исходя из этой системы равенств, построим систему параметрических функций, допускающих несмещенное оценивание параметров функции отклика

^r₀=₀ +₁₂₄, ^r₁=₁ + ₁₂, ^r₂= ₂ +₁₄, ^r₃=₃ + ₁₂₃₄.

^r₄=₄ + ₁₂, ^r₅= ₁₃ +₂₃₄, ^r₆=₂₃ + ₁₃₄, ^r₇=₃₄ + ₁₂₃.

Если для оценивания параметров функции отклика применяется (1/4)-реплика или реплики более высокой дробности, то система смешивания линейных эффектов и эффектов взаимодействий между собой будет более сложной, поскольку для задания (1/g)-реплик (g>2) необходимо не менее двух генерирующих соотношений.

Пусть четверть-реплика 2^5-2 задается генерирующими соотношениями x₄=x₁x₂ и x₅=x₁x₂x₃. Умножив их на x₄ и x₅ соответственно, получим определяющие контрасты

1=x₁x₂x₄; 1=x₁x₂x₃x₅.

Если их перемножим, то получим еще один определяющий контраст

1=x₃x₄x₅.

Затем получаем обобщенный определяющий контраст

1=x₁x₂x₄=x₁x₂x₃x₅=x₃x₄x₅.

Для получения системы равенств, отображающих систему смешивания независимых переменных и взаимодействий, следует умножать отображенный определяющий контраст последовательно на независимые переменные x₁, x₂, x₃, x₄, x₅. Система уравнений будет иметь следующий вид:

x₁=x₂x₄=x₂x₃x₅=x₁x₃x₄x₅;

x₂=x₁x₄=x₁x₃x₅=x₂x₃x₄x₅;

x₃=x₁x₂x₃x₄=x₁x₂x₅=x₄x₅;

x₄=x₁x₂=x₁x₂x₃x₄x₅=x₃x₅;

x₅=x₁x₂x₄x₅=x₁x₂x₃=x₃x₄;

x₁x₃=x₂x₄x₃=x₂x₅=x₁x₄x₅;

x₁x₅=x₂x₄x₅=x₂x₃=x₁x₃x₄.

С учетом обобщенного определяющего контраста получено восемь равенств, которые однозначно определяют систему параметрических функций смешивания эффектов:

^r₀=₀+ ₁₂₄ + ₃₃₅ + ₁₂₃₅; ^r₁=₁ + ₂₄ + ₂₃₅ + ₁₃₄₅;

^r₂=₂+ ₁₄ + ₁₃₅ + ₂₃₄₅; ^r₃=₃ + ₄₅ + ₁₂₅ + ₁₂₃₄;

^r₄=₄+ ₁₂ + ₃₅ + ₁₂₃₄₅; ^r₅=₅ + ₃₄ + ₁₂₃ + ₁₂₄₅;

^r₆=₁₃+ ₂₅ + ₁₄₅ + ₂₃₄; ^r₇=₁₅ + ₁₃ + ₁₃₄ + ₂₄₅.

Получен вектор , оценивание которого возможно по данным вектора наблюдений Y=(y₁,y₂,…,y₈)^T и данным матрицы X⁰

,

которая является матрицей ортогонального планирования и ее rankX⁰=8.

Проблема выбора дробных планов является основной при планировании факторных экспериментов. Ее решение направлено на нахождение таких дробных реплик 2^k-g, которые бы позволили получить несмещенные МНК-оценки для всех неизвестных параметров функции отклика. Отметим особенности применения дробных реплик:

- число опытов N₀<p+1  числа неизвестных параметров модели;

- модель наблюдений является моделью неполного ранга, равного N₀;

- матрица независимых переменных приведенной модели полного ранга является матрицей ортогонального планирования;

- система параметрических функций, допускающих оценку, выводится из определяющих контрастов.