Контрольные задания

1. Приведите определения системы.

2. Дайте определение понятиям «структура», «состояние», «связи», «элемент», «равновесие», «устойчивость», «развитие».

3. Дробный факторный эксперимент

3.1. Определение дробных реплик

Число опытов в ПФЭ превышает число коэффициентов линейной модели, причем тем больше, чем больше факторов. Если можно ограничиться линейным приближением, то число опытов можно сократить, используя для планирования дробные реплики от полного факторного эксперимента [14].

С ростом числа переменных k число опытов N быстро растет, а при большом числе k реализация ПФЭ 2^k становится практически невозможной. Также с ростом N увеличивается число взаимодействий и их порядок в формуле (2.4).

Кроме того, при анализе функционирования объекта может быть известно, что в уравнении (2.4) эффектами воздействия высоких порядков можно пренебречь либо они не существуют. Следовательно, число опытов для нахождения оценок неизвестных коэффициентов уравнения (2.4) может быть уменьшено. Это производится с помощью применения дробных факторных экспериментов (ДФЭ), представляющих собой дробные реплики от ПФЭ.

Для построения дробного факторного плана типа 2^k-p из множества k отбирают (k-p) основных факторов, для которых строят полный факторный план с матрицей Х_k-p.

Этот план дополняют затем р столбцами, соответствующими оставшимся факторам. Каждый из этих p столбцов получается как результат поэлементного перемножения не менее двух и не более (k-p) определенных столбцов, соответствующих основным факторам.

Для определения столбца образования каждого из р столбцов дробного факторного плана вводится понятие генератора плана [13]. Генератор представляет собой произведение основных факторов, определяющее значение элементов каждого из дополнительных столбцов матрицы плана. Очевидно, что в случае плана типа 2^k-p должно иметься р генераторов.

Допустим, что нужно получить линейное приближение некоторого небольшого участка поверхности отклика при трех независимых переменных. Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании для ПФЭ типа 2² произведение x₁x₂ обозначить третьим фактором x₃. Будет получена матрица планирования, представленная в табл. 1.1.

Таблица 1.1

Матрица планирования

№ опыта	x0	x1	x2	x3=x1x2	Кодовое обозначение	Y
1 2 3 4	1 1 1 1	-1 1 -1 1	-1 -1 1 1	1 -1 -1 1	(1) a b ab	y1 y2 y3 y4

Функция отклика имеет вид

. (3.1)

Эффекты парных и тройного взаимодействия равны нулю, а это позволяет уменьшить число опытов вдвое по сравнению с ПФЭ 2³ (N=8) в случае, если бы эти эффекты были бы отличны от нуля.

Матрица плана в этом случае имеет вид

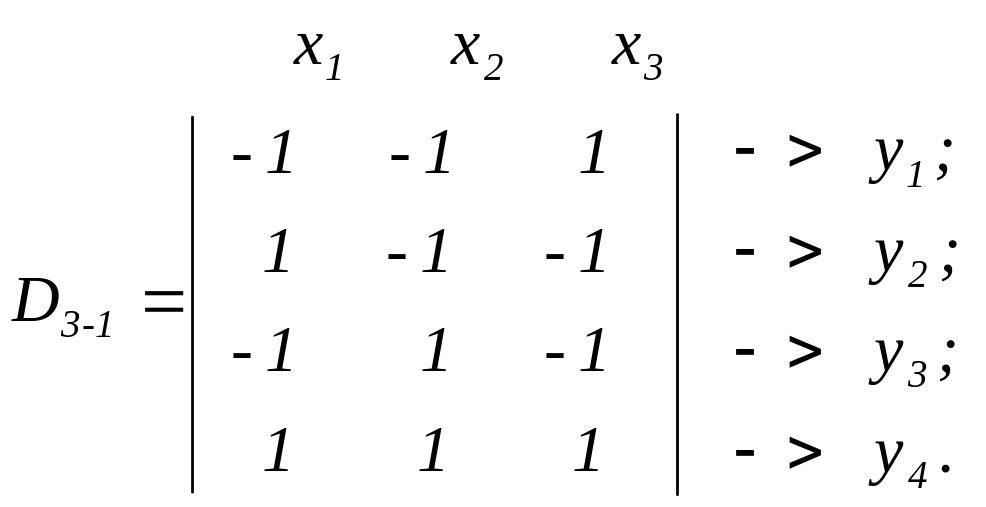
Матрица D_3-1 получена из матрицы D₃ ПФЭ 2³ путем вычеркивания строк (1, -1, 1), (-1, 1, 1), (-1, -1, -1), (1, 1, -1). Построенный ДФЭ представляет собой полуреплику (1/2 реплику) от ПФЭ 2³. Матрица D_3-1 обладает, как и матрица D₃, свойствами симметрии, нормирования и попарной ортогональности:

.

Таким образом, для построения полуреплики 2^3-1 взяты не произвольные точки плана 2³. Переменная х₃ в точках плана удовлетворяет соотношению х₃=x₁x₂, которое называется генерирующим. Еще одна полуреплика может быть построена, если взять генерирующее соотношение х₃=-х₁x₂. Чтобы построить матрицу D_2-1, следует сформировать матрицу D₂ ПФЭ 2², а затем с помощю генерирующего соотношения построить вектор-столбец Х₃.

Матрица Х будет ортогонального планирования

.

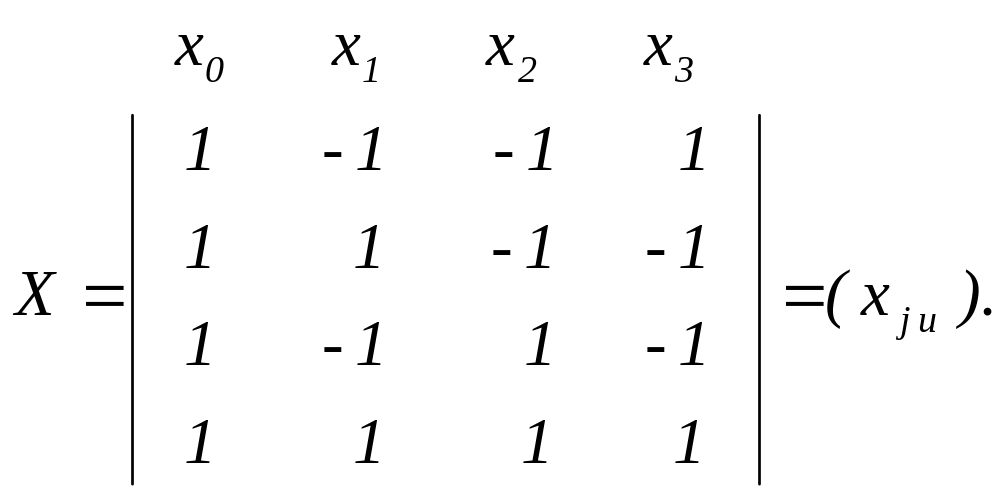МНК ‑ оценки неизвестных параметров _j функции (3.1) определяются

.

Оценки {_j} некоррелированы и их дисперсия равна

.

Для построения дробного факторного плана при N=4 исходим из полного факторного плана 2³ для факторов х₁, х₂ и х₃ и дополняем его столбцами, образованными произведениями столбцов плана 2³ х₁х₂, х₁х₃, х₂х₃, х₁х₂х₃. Эти произведения могут использоваться в качестве генераторов для дробных планов. Используя один из четырех возможных генераторов, можно построить четыре различных дробных плана типа 2^4-1:

x₄=x₁x₂, x₄=-x₁x₂; x₄=x₁x₃, x₄=-x₁x₃; x₄=x₂x₃, x₄=-x₂x₃;

x₄=x₁x₂x₃, x₄=-x₁x₂x₃.

По сравнению с 2⁴=16 опытами полного факторного эксперимента полученный дробный план состоит из 2^4–1=8 опытов.

Функции отклика (2.3) ПФЭ 2³ соответствует матрица независимых переменных

Матрица ДФЭ 2^4–1 с генерирующим соотношением x₄=x₁x₂ будет иметь вид:

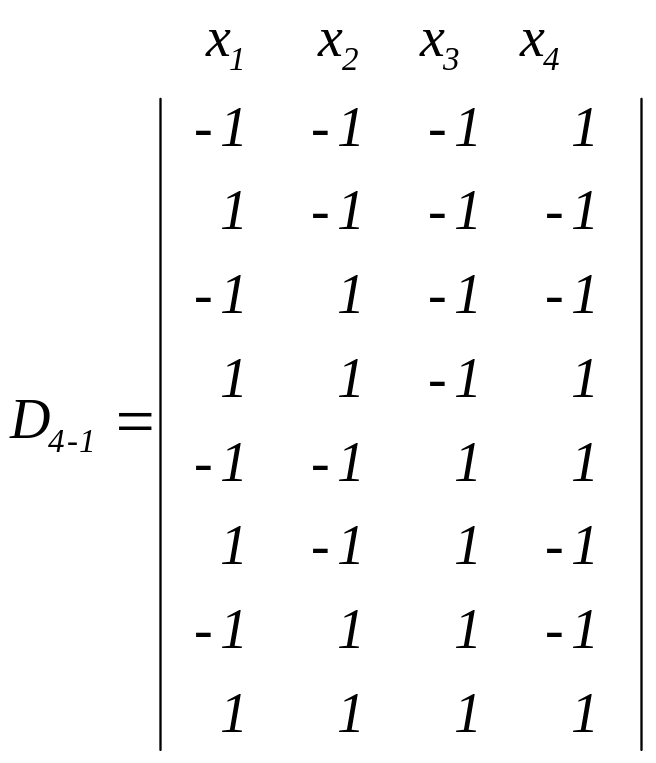
Множество D_4–1 обладает свойствами симметрии, нормирования и попарной ортогональности, поэтому оценки функции отклика

имеют единственные решения

Множество всех генерирующих соотношений для полуреплик 2^k-1 совпадает со множеством всех взаимодействий до (k-2)-го порядка включительно, взятых со знаком плюс и минус. Число различных полуреплик 2^k-1 определится формулой v=2(2^k-1-k).

Наряду с дробным факторным планом 2^k-1 в исследованиях могут быть использованы также дробные факторные планы 2^k-g. Дробный факторный план 2^k-2 называется четверть-репликой от ПФЭ 2^k.Для построения четверть-реплики ПФЭ 2^k используются два генерирующих соотношения.

Рассмотрим построение четверть-реплики 2^5-2. Матрица плана D_5-2 четверть-реплики строится исходя из матрицы плана ПФЭ 2³ с применением двух генерирующих соотношений, определяющих переменные x₄ и x₅.

Для построения дробной реплики 2^5-2 может быть использовано 24 варианта генерирующих соотношений:

1) x₄ = x₁x₂, x₅ = x₁x₂ x₃; 2) x₄ = x₁x₂, x₅ = - x₁x₂ x₃;

3) x₄ = - x₁x₂, x₅ = x₁x₂ x₃; 4) x₄ = - x₁x₂, x₅ = - x₁x₂ x₃;

5) x₄ = x₁x₃, x₅ = x₁x₂ x₃; 6) x₄ = x₁x₃, x₅ = - x₁x₂ x₃;

7) x₄ = - x₁x₃, x₅ = x₁x₂ x₃; 8) x₄ = - x₁x₃, x₅ = - x₁x₂ x₃;

9) x₄ = x₂x₃, x₅ = x₁x₂ x₃; 10) x₄ = x₂x₃, x₅ = - x₁x₂ x₃; и т. д.

Общее число взаимодействий до (k-3)-го порядка включительно определится =2^k-3(k-1), а число всех дробных реплик 2^k-2 равно .

Воспользуемся генерирующими отношениями x₄=x₁x₂, x₅=x₁x₂x₃, построим матрицу дробного факторного плана 2^5-2

Примем, что функция отклика имеет вид

,

матрица независимых переменных является матрицей ортогонального планирования. Оценки неизвестных коэффициентов функции отклика определятся

.

Очевидно, что по сравнению с ПФЭ 2⁵ в ДФЭ 2^5-2 число опытов уменьшено в четыре раза.

Методом математической индукции можно определить, что число дробных реплик 2^k-g равно

,

где _k-(g-1) ‑ число всех взаимодействий до [k-(g+1)]-гo порядка включительно, причем _k-(g-1)=2^k-g-[k-(g-1)].