6.2. Применение нормального закона для оценки вероятности и проверки гипотез

6.2.1. Нормальное распределение как приближение биноминального. В теории вероятностей известно теоретическое биноминальное распределение, согласно которому вероятность P того, что в проведенных n опытах дискретная случайная величина X будет равна x определится по формуле

. (6.12)

Если случайная величина X может принимать значения 0, 1, 2, …, n, то вероятность

, (6.13)

где q=1-p.

При большиз значениях n биноминальное распределение с хорошим приближением может быть описано с помощью нормального распределения (см. табл. 1.2) с тем же центром и с той же дисперсией, что и у биноминального распределения [ ]. Данное положение определено теоремой Лапласа: если n неограниченно возрастает, то при любом z

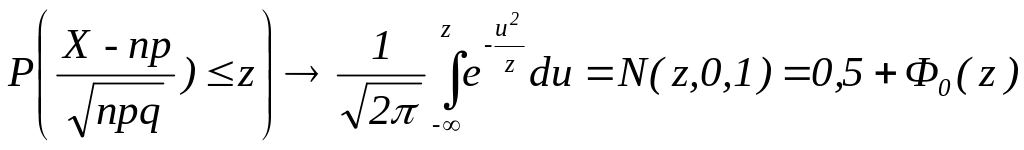, (6.14)

т.е. вероятность того, что нормированная величина X, распределенная по биноминальному вопросу, будет меньше заданного числа z, стремящегося с ростом n к нормальной функции распределения.

Отметим, что Ф₀(z)  определенный интеграл с переменным верхним пределом вида

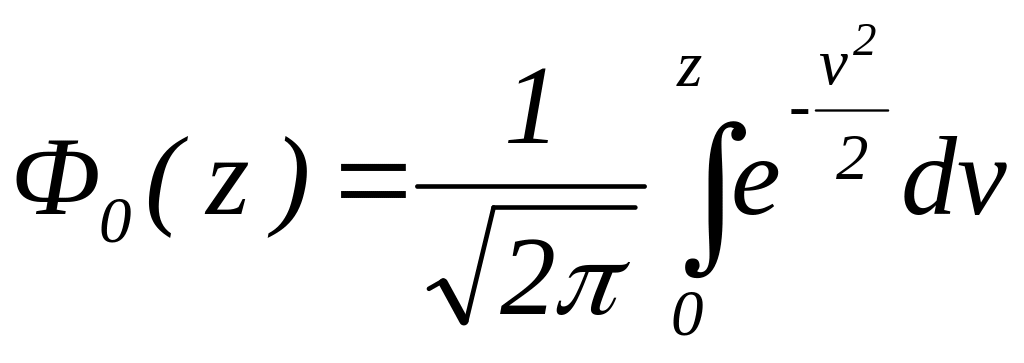
выражающий площадь под кривой n(z; 0; 1) в промежутке от 0 до z (см. рис. 6.4), носит название нормированной функции Лапласа, а  среднее квадратическое отклонение величины X и X’=X - np от центра.

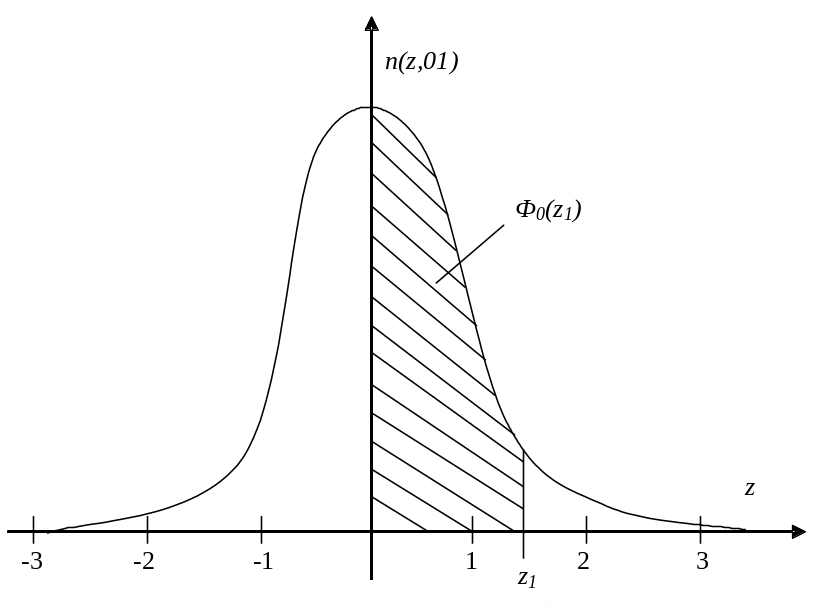
Рис. 6.4

Вместо величины X  числа положительных исходов опытов независимых испытаний рассматривают величину X/n  частость появления случайного события. Тогда формула (6.14) примет вид

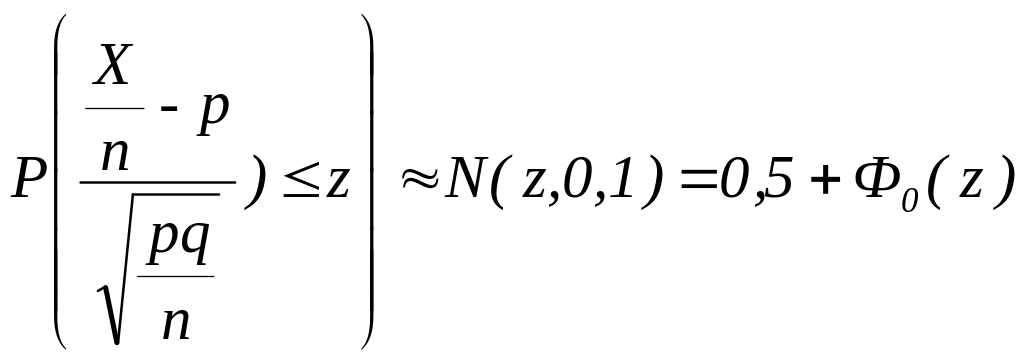, (6.15)

Если рассматривать случайную величину X/n=w_n – частость, то её распределение согласно (6.15) приближенно описывается при больших n нормальным распределением N(z;p;_n), при n. Вид распределения показан на ри. 6.5. Это распределение имеет вид иглы. Основная масса вероятности распределения сконцентрирована в непосредственной близости от центра в интервале (p-, p+).

Рис. 6.5

Бернулли сформулировал теорему: вероятность того, что уклонение частости X/n от вероятности p не превзойдет по абсолютному значению сколь угодно малого , стремиться к единице при возрастании n.

6.2.2.Доверительные интервалы для неизвестной вероятности. После выполнения независимых n опытов определена частность w_n=X/n событий X=А. Теоретическое значение вероятности P(A)=p неизвестно, но при n можно полагать p X/n=w_n.

Так как величина w_n есть одно из возможных значений случайной величины W_n, то желательно знать вероятные пределы погрешности приближенного равенства p X/n=w_n.

Если n достаточно велико, то согласно (6.15) можно считать, что случайная величина

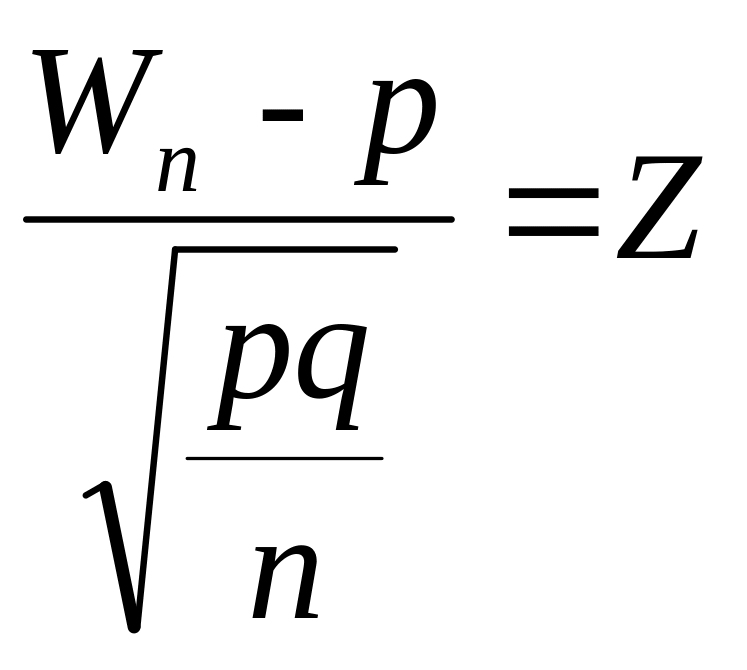
приближенно следует нормальному закону. Тогда для каждого значения вероятности P можно найти такое число t_p>0, что

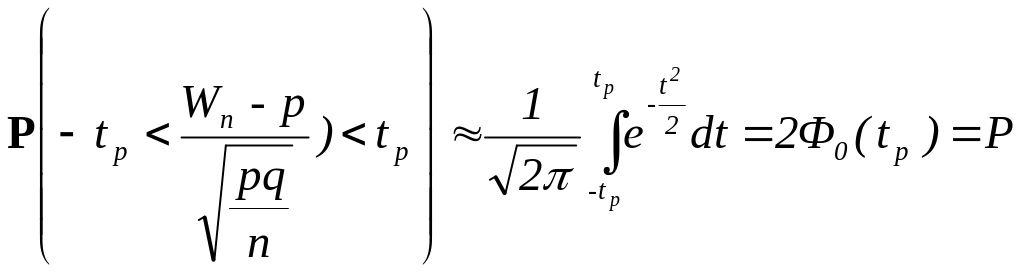, (6.16)

Число t_p приближенно определяется по таблицам функции Ф(z) [].

Доверительный интервал, отвечающий заданному уровню доверительной вероятности P, определяется следующим образом.

Практически достоверным будет считать событие, имеющее вероятность P или большую, при следующем предположении. Вероятность P задана так близко к 1, что можно пренебречь событиями, имеющими вероятность, не большую 1-P, т.е считать их практически невозможными. Тогда определена веротяность W_n нахождения частости w_n в заданных пределах

, (6.17)

так как согласно выбору пределов t_p практически достоверно, что при каждом P выполнено условие

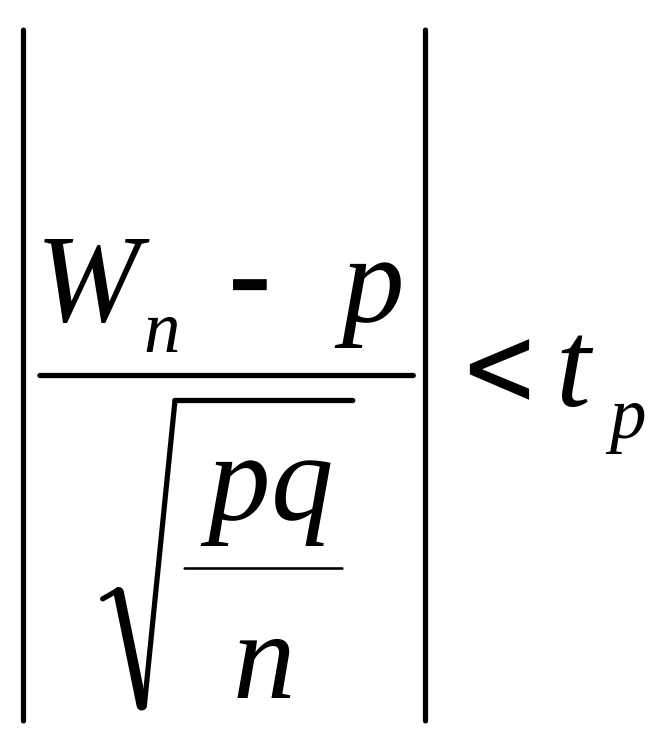. (6.18)

Неравенство (6.17) имеет эквивалентный вид

,

или

,

или в виде неравенства относительно переменной p

, (6.19)

Решая квадратное уравнение в левой части неравенства (6.19), можно получить два действительных корня

, ,

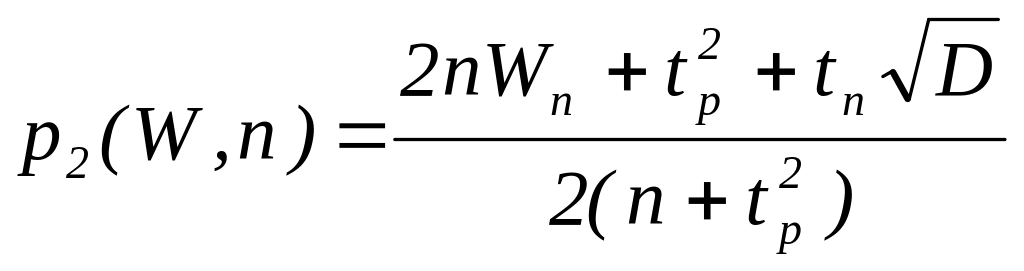где , 0<p₁(W,n)<p₂(W,n)<1.

Если значение вероятности p появления события А находится между p₁(W,n) и p₂(W,n), т.е.

p₁(W,n)<p<p₂(W,n), (6.20)

то выполняются (6.19 и (6.17), т.е. с одной и той же вероятностью случайная величина W_n входит в левую и правую части неравенства (6.20).

Такм образом, получен интервал [p₁(W,n), p₂(W,n)], покрывающий с вероятностью P неизвестное значение p, который называется доверительным интервалом.

Рассмотрим пример [ ]. При числе n=200 независимых опытов событие А появилось M=88 раз. Определим доверительные границы с значением вероятности P=0,95 для вероятности P(А).

В табл. 6.1 приведены значения вероятностей при нормальном распределении.

Таблица 6.1

Вероятности при нормальном распределении

Границы интервалов относительно математического ожидания а	Вероятность попадания в интервал
а - , а + , а - 2, а + 2, а - 3, а + 3	0,6826968 % 0,9545095 % 0,9973099,7 %

Из табл. 6.1 следует, что при P0,95 имеем значение t_0,95=2. Определим частость w_n=M/n=88,200=0,44. Тогда:

=14,18;

;

.

Таким образом, доверительной вероятности P=0,95 соответствует интервал (0,37< p <0,51)

Особо отметим, что данный метод поиска доверительного интервала пригоде при больших значениях n; согласно [ ] при значении

npq>9. (6.21)

Если условие (6.21) не выполняется, то поступают следующим образом.

Сумма начальных членов биноминального распределения (6.12) имеет вид

. (6.22)

После дифференцирования (6.22) по аргументу p, получим

. (6.23)

При постоянных значениях n и M производная функции S_nM(p) отрицательная при 0<p<1. Эта функция монотонно убывает от значения 1 при p=0 к значению 0 при p=1. Следовательно функция S_nM(p) примет единственный раз любое значение  между нулем и единицей.

Обозначим значение вероятности p, соответствующее значению S_nM(p) функции, через , т.е. уравнение (6.22) приравняем значению 

. (6.24)

Если в результате опытов получена частота M события А, то утверждение о том, что верхний доверительный предел для искомой вероятности p, гаранрируемый с вероятностью 1-, равен , будет ошибочно с вероятностью, не большей .

Таким образом, в качестве верхнего доверительного предела с вероятностью ошибки, меньшей , следует взять  корень уравнения (6.24).

Аналогичным сопособом определяется нижний доверительный предел, отвечающий доверительной вероятности 1-, который находится из решения уравнения

. (6.25)

Решение уравнения (6.25) обозначим через p_M. Интервал ( ) будет доверительным интервалом для неизвестной вероятности p, построенной по частоте M и отвечающий доверительной вероятности, не меньшей 1-2.