Часть 2. Обработка экспериментальных данных

6. Обработка статистических данных

6.1. Сведения из теории вероятностей

В теории вероятностей существует понятие «испытание», под которым понимается осуществление определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз. Явления происходящие при реализации этого комплекса называются событиями. В результате испытаний в зависимости от случайных обстоятельств может произвойти то или иное событие из некоторого множества. События должны отражать качество проводимых испытаний, т.е. обладать репрезентативностью.

Пусть проведено N опытов в одних и тех же условиях. Событие X в серии опытов произошло n_X раз. Значение характеризует частоту появления события X. Отношение n_A/N числа появления событий X к общему числу событий N называют частостью события или относительной частотой.

Частость события X является оценкой вероятности p_X появления этого события и считают, что .

Случайные величины, принимающие отделенные друг от друга значения называют дискретными случайными величинами. Для каждого значения X_i дискретной случайной величины существует значение вероятности p_i её появления.

Упорядоченные значения вероятностей p_i называют дискретным распределением вероятностей (или просто распределением) случайной величины X.

Для дискретной случайной величины X определяют числовую характеристику в виде математического ожидания, которую обозначают символом МX. Смысл математического ожидания иллюстрирован на рис. 6.1.

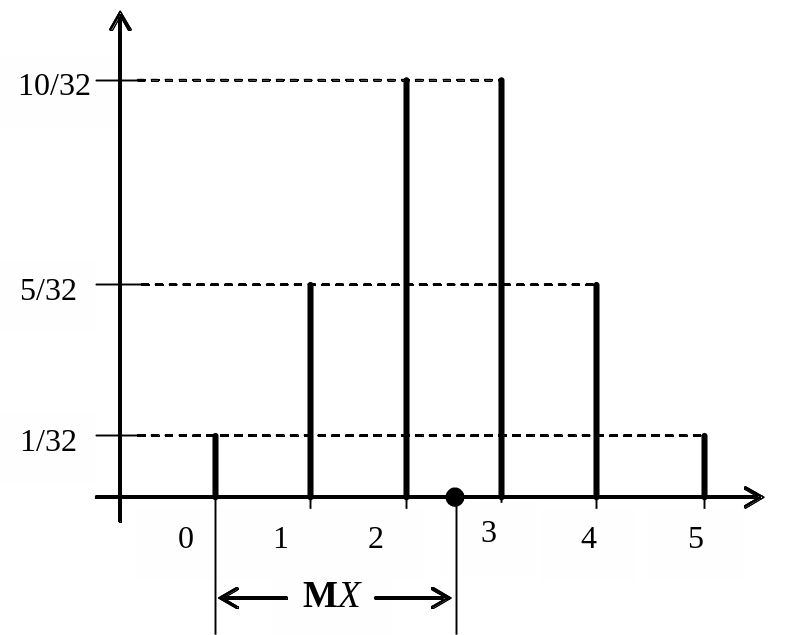
Рис. 6.1

Точка МX рассматривается, как центр группирования случайной величины X или центр тяжести. Известно, что абцисса центра тяжести может быть определена путем подсчета средней «взвешенной» абцисс точек (1, 2, 3, 4, 5). Взвешивание значений величины получается путем умножения каждого её значения на его «вес». Отсуда вытекает физический смысл формулы для определения математического ожидания МX

. (6.1)

Могут рассматриваться целые степени X^k случайной величины X. В этом случае математическое ожидание МX^k называют моментом k–го порядка случайной величины X и определяют формулой

. (6.2)

Модой теоретического распределения случайной величины X называют наиболее вероятное её значение и обозначают символом МоX.

В теории вероятностей существует понятие центрированной случайной величины X=X-МX, еще называемое отклонением случайной величины X

Моменты центрированной случайной величины X назвают центральными моментами случайной величины X.

Центральный момент k–го порядка теоретического распределения случайной величины X обозначают, как правило греческими буквами

, (6.3)

т.е. центральный момент k–го порядка представяляте среднюю величину (математическое ожидание) k–й степени отклонения случайной величины X от центра.

Центральный момент 2–го порядка называют дисперсией и обозначают символам МоX. Название «дисперсия» появилось по аналогии с механикой, как мера рассеивания. Дисперсию можно истолковать, как момент онерции «масс вероятностей» (см. рис. 6.2).

В электротехнике дисперсия имеет простой смысл: исходя из определения мощности P=i²R (i  мгновенное значение силы изменяющегося тока, R  сопротивление), дисперсию можно трактовать как среднее значение мощности флуктуций, которая рассеивалась бы на единице сопротивления.

Согласно определения (6.3), дисперсия имеет размерность, определяемую квадратом размерности случайной величины X. Чтобы получить характеристику рассеивания, имеющую размерность, одинаковую с размерности случайной величины X и её математическим ожиданием, применяют положительный корень квадратный из дисперсии

. (6.4)

Величину _X назвают средним квадратическим или стандартным отклонением.

В качестве относительной характристики рассеивания применяют коэффициент вариации, представляющий среднее квадратическое отклонение в процентах к математическому ожиданию

. (6.5)

Коэффициент вариации показывает, насколько велико рассеивание по сравнению со средним значением случайной величины X.

На практике при обработке статистических данных ещё применяют центральные моменты третьего и четвертого порядков, а моменты более бысоких порядков не используются.

Центральный момент третьего порядка применяют для числового измерения ассиметрии распределения, примером которого является распределение Релея 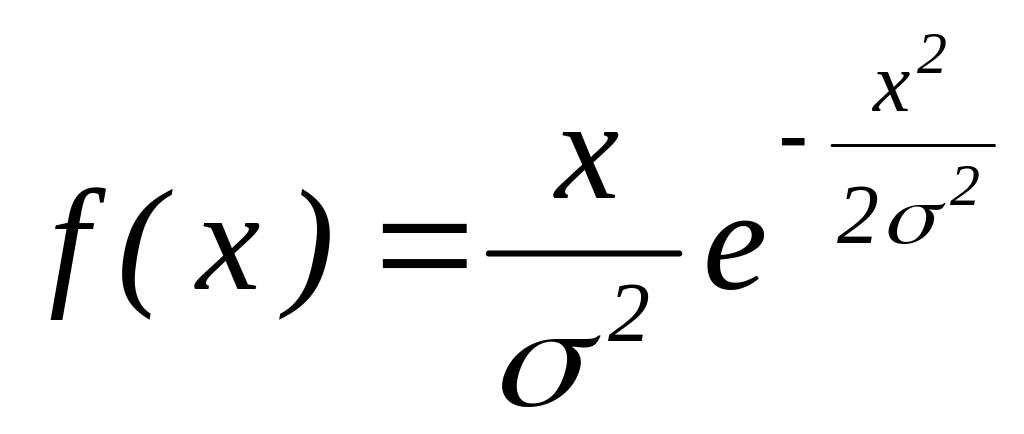. График распределения Релея показан на рис. 6.2.

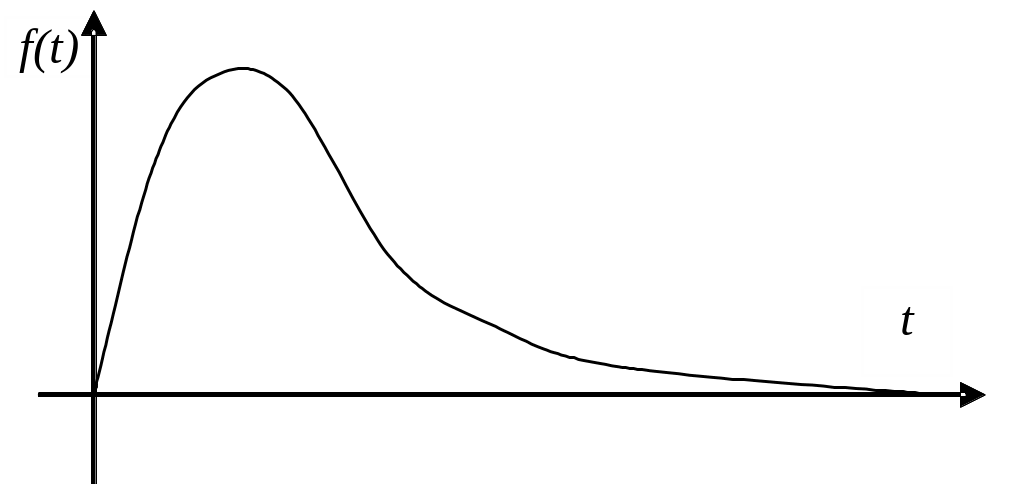
Рис. 6.2

Для перехода к безразмерной характеристики центральный момент третьего порядка делят на куб среднего квадратического отклонения. Показатель ассиметрии в этом случае определяется выражением

. (6.6)

В качестве характристики большего или меньшего подъема графика (болшей или меньшей вершинности) по сравнению с графиком нормального распределения применяют показатель _k, определяемый формулой

. (6.7)

Случайные величины, значения которых непрерывно заполняют некоторый отрезок, называют непрерывными случайными величинами. Для непрерывной случайной величины существует понятие «функция распределения вероятностей», которая обозначается F(x)=P(X<x).

Для непрерывно распределенной случайной величины X математическое ожидание определится по формуле

, (6.8)

где f(X)  функция распределения плотности вероятности случайной величины X.

Математическое ожидание МX^k (момент k–го порядка) непрерывной случайной величины X определяют формулой

. (6.9)

Центральный момент k–го порядка непрерывной случайной величины X определяют формулой

. (6.10)

Дисперсия непрерывной случайной величины X определится по формуле

. (6.11)

Для оценки функции распределения вероятностей в результате проведения испытаний получают эмпирическую кумулятивную функцию распределения, возможный вид которой показан на рис. 6.3.

В табл. 1.1 приведен результат проведения испытаний (опытов), попадания значений случайной величины А в отрезки, заданные от нуля до границы оценки D(I). В счетчиках K(I) записаны результаты частот попадания в интервалы, определенные границами D(I).

Частости попадания случайной величины X в I-й интервал определяются по формуле

так как в счетчике K(8) определено общее число опытов.

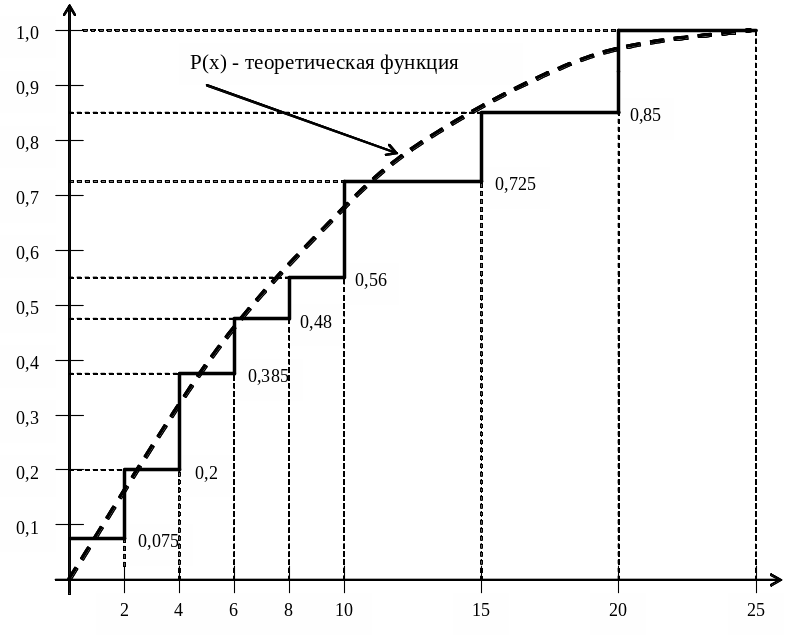
Рис. 6.3

Таблица 1.1

Статистические данные результатов моделирования

Границы оценки	D(1) 2	D(2) 4	D(3) 6	D(4) 8	D(5) 10	D(6) 15	D(7) 20	D(8) 25
Номер счетчика	К(1)	К(2)	К(3)	К(4)	К(5)	К(6)	К(7)	К(8)
Частота события	37	100	193	240	280	362	425	500

По полученным значениям строится гистограмма кумулятивной эмпирической функции распределения так, что в точке I (I=2,4,5,…,25) значение функции равно

.

Затем выдвигается гипотеза, состоящая в том, что найденная кумулятивная эмпирическая функция распределения может быть аппроксимирована теоретическим распределением F(x) (см. рис. 6.3). Проверка гипотезы осуществляется по критерию ².

В табл. 1.2 приведены некоторые законы распределения непрерывных случайных величин и их характеристики  математическое ожидание MX, дисперсия DX [4].

Таблица 1.2

1. Равномерное распределение
, F(x)=(x‑a)/(b‑a)		MX =(a+b)/2, DX =(a‑b)2/12
2. Экспоненциальное распределение
, F(x)=1–ex, x0		MX =1/, DX =1/2
3. Нормальное распределение
		MX =a, Dx=2
4. Распределение Рэлея
,		,
5. Распределение Коши
,		Mx, Dx не существуют
6. Распределение Эрланга
, x0,	MX=m/a, DX =m/a2