Контрольные задания
1. Приведите определения системы.
2. Дайте определение понятиям «структура», «состояние», «связи», «элемент», «равновесие», «устойчивость», «развитие».
3. Какими способами исследуются аналитические модели?
4. Как формально определяются векторы состояний, входных и выходных параметров?
5. Информационное обеспечение для задач планирования эксперимента
Для решения задачи поиска экстремума функции отклика с применением метода крутого восхождения можно разработать инфориационное обеспечение, т.к. процесс решения задачи достаточно просто алгоритмизируется. Ниже приводится пример работы с инормационным обеспечением для решения этой задачи.
Первым шагом при использовании данного информационного обеспечения является ввод начальных данных. На рис. 5.1 приведен вид диалогового окна с формой ввода значений задачи.
Рис. 5.1
На рис. 5.1 левая таблица представляет собой набор факторов, т.е. измеряемых переменных величин, принимающих в конкретный момент времени определенное значение.
Правая таблица результаты наблюдений для каждой серии экспериментов. Ещё правее находятся пункты настройки, где можно выбрать количество настраиваемых наборов факторов, количество опытов и количество серий экспериментов.
Для примера анализа работы информационного обеспечения взят набор факторов, показанный в табл. 5.1.
Таблица 5.1
№ опыта |
x1 |
x2 |
1 2 3 4 |
-1 +1 -1 +1 |
-1 -1 +1 +1 |
Результаты наблюдений:
- первая серия измерений:
y1 = 95,6; y2 = 90,6; y3 = 84,3; y4 = 83;
- вторая серия:
y1 = 94,4; y2 = 89,4; y3 = 85,7; y4 = 81.
Как видим, количество опытов 4. На рис. 5.2 представлена форма с введенными значения опытов.
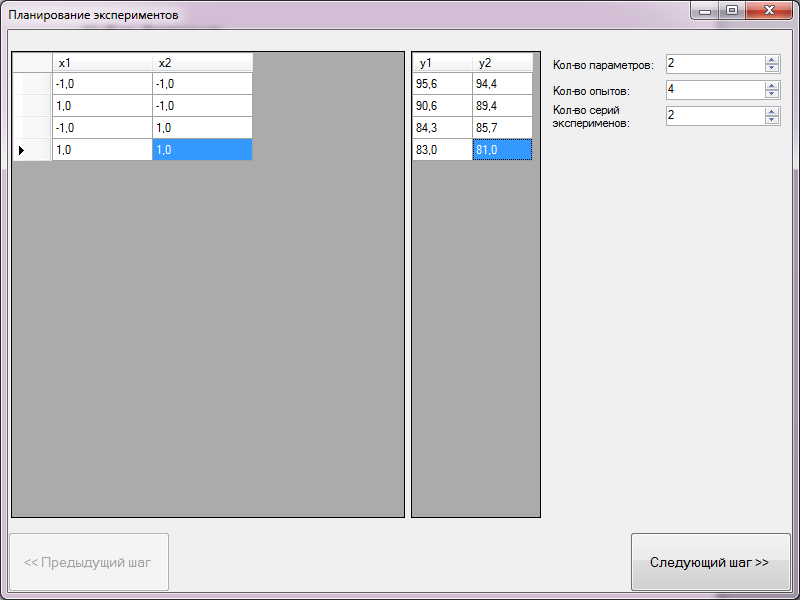
Рис. 5.2
После ввода значений осуществляется переход к диалоговому окну, в котором вводится область определения факторов (см. рис. 5.3).
Рис. 5.3
В этом окне вверху выводится уравнение регрессии, соответствующее введенным ранее значениям.
Для дальнейших расчетов требуется ввести основной уровень факторов и интервал варьирования факторов.
Основной уровень исходная точка для построения плана эксперимента. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.
Интервал варьирования необходим для расчета параметров крутого восхождения и является начальным шагом для градиентного метода. Данные, взятые для примера, приведены в табл. 5.2. На рис. 5.4 показано диалоговое окно ввода области определения факторов.
Таблица 5.2
Уровень |
x1 |
x2 |
Основной уровень |
1,5 |
7,0 |
Интервал варьирования |
0,5 |
1,0 |
После того, как все значения введены, начинается поиск экстремума по уравнению регрессии. Окно поиска экстремума приведено на рис. 5.5.
Рис. 5.4
Рис. 5.5
Пользователь при расчете каждого шага может менять значение коэффициента шага крутого восхождения α, возвращаться назад и производить поиск экстремума с измененными значениями, что отображено на рис. 5.6.
Рис. 5.6