4.4. Пример расчета крутого восхождения

Предположим, что в результате проведения полного факторного эксперимента типа 2² получены следующие результаты наблюдений y_u:

первая серия: y₁=95,6; y₂=90,6; y₃=84,3; y₄=83;

вторая серия: y₁=94,4; y₂=89,4; y₃=85,7; y₄=81.

В табл. 4.1 приведено среднее значение y*.

Таблица 4.1

№ опыта	x0	x1	x2	y*
1 2 3 4	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	95,0 90,0 85,0 82,0

Для вычисления коэффициентов регрессии определим следующие матрицы:

; ; .

Определим матрицу системы нормальных уравнений и определим оценки коэффициентов:

,

,

.

Следовательно,

y=88–2x₁–4,5x₂ . (4.1)

Область определения факторов задана табл. 4.2.

Таблица 4.2

Уровень	x1	x2
Основной уровень	1,5	7,0
Интервал варьирования	0,5	1,0
Верхний уровень	2,0	8,0
Нижний уровень	10	6,0

Для проверки гипотезы адекватности выбранной модели используем F-критерий

,

где: -   дисперсия адекватности [14, c.201];

-   дисперсия воспроизводимости;

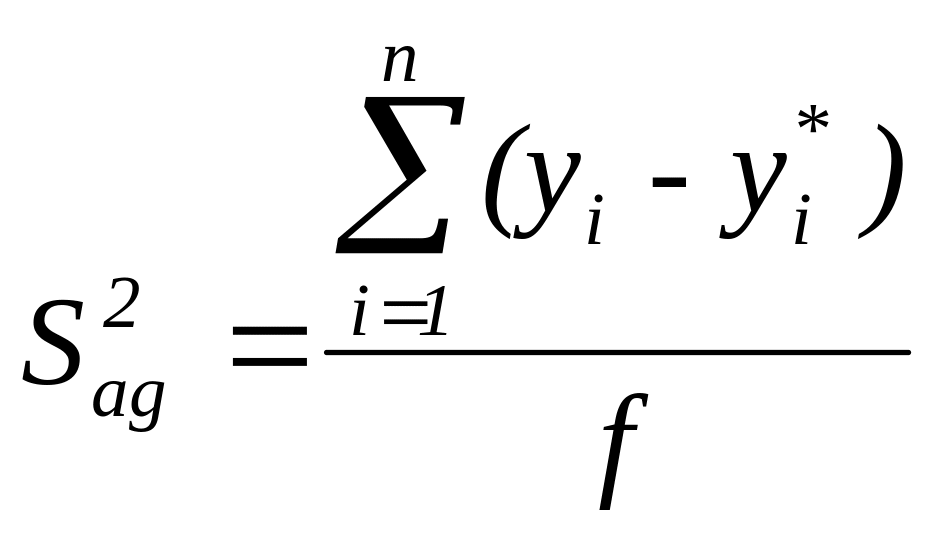-  , f=N-(k+1)=4-(2-1)=1  число степеней свободы.

Для расчета составим табл. 4.3 расчета остаточной суммы квадратов.

Таблица 4.3

№ опыта	x0	x1	x2	y	yi	yi-y*	y-y*
1 2 3 4	1 1 1 1	-1 1 -1 1	-1 -1 1 1	95 90 85 82	94,5 90,5 85,5 81,5	-0,5 0,5 0,5 -0,5	0,25 0,25 0,25 0,25

Для вычисления дисперсии воспроизводимости составим расчетную табл. 4.4.

Следовательно, [14. С. 162:

.

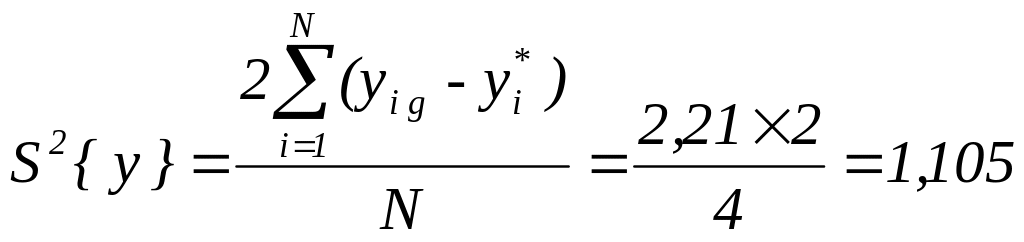Таблица 4.4

№ опыта	y’	y’’	y	y’	y’’
1 2 3 4	95,6 90,6 84,3 83	94,4 89,4 85,7 81	95 90 85 82	0,6 0,6 0,7 1,0	0,36 0,36 0,49 1,0	2,21

Вычислим значение F-критерия [14. С.202]:

.

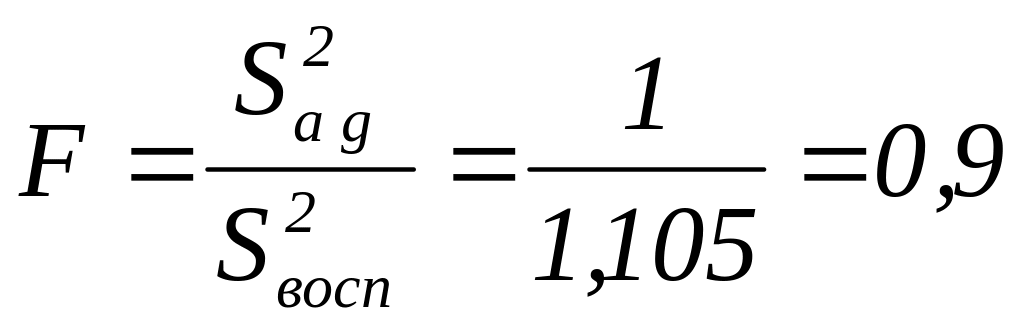Табличное значение критерия Фишера для числа степеней свободы 1,4 и 5-го уровня значимости [14. C.04] равно 7,7. Поэтому гипотеза адекватности линейной модели может быть принята как справедливая [14, с.203].

Проверку значимости величины дисперсии вычислим по формуле [14, с.207]

.

Определим доверительный интервал: b_j=tS{b_j}=-t S{b_j}, где t  табличное значение критерия Стьюдента [14. С.208] при числе степеней свободы, с которыми определялась S²{y}, и выбранном уровне значимости (0,05). При f=N=4 имеем b_j=2,7760,37=1,03.

Отсюда видно, что вычисленные коэффициенты значимости, т.е. их абсолютные значения, больше доверительного интервала [14. С. 209].

Рассмотрим этапы расчета крутого восхождения. Результаты расчетов будем фиксировать в табл. 4.5.

1. Определим составляющие градиента. Для шага варьирования 0,5 и 1,0 имеем

b₁x₁=-20,5=-1; b₂x₂=-4,51,0=-4,5.

Прибавим составляющие градиента к основному уровню факторов

x₁=1,5-1,0=0,5.

Таблица 4.5

	x1	x2	y*
Основной уровень Интервал варьирования Верхний уровень Нижний уровень	1,5 0,5 2,0 1,0	7,0 1,0 8,0 6,0
Кодированные значения переменных	x1	x2
Опыты: 1 2 3 4	-1 -1 -1 -1	-1 -1 -1 -1	95,0 90,0 85,0 82,0
bj bj, умноженное на интервал варьирования Шаг при изменении x2 на 0,5 Округление	-2,0 -1,0 -0,11 -0,1	-4,5 -4,5 -0,5 -0,5
Опыты в направлении крутого восхождения
5 6 7 8 9	1,4 1,3 1,2 1,1 1,0	6,5 6,0 5,5 5,0 4,5

Опыт 5

x₂=7,0-4,5=2,5, x₁=0,5-1,0=-0,5.

Опыт 6

x₂=2,5-4,5=-2,0.

Условия опыта 6 не реальны, так как значения x_j при этом выходят за границы допуска. Следовательно, шаг движения велик.

2. Воспользуемся условием: умножение составляющих градиента на любое положительное число дает точки, лежащие на градиенте.

В данной задаче удобно изменить х₂ на 0,5, т.е. уменьшить составляющую градиента в 9 раз. Во столько же раз уменьшается и составляющая градиента по первому фактору (-0,11). Изменению составляющих градиента соответствует в табл.6.8 строка «Шаг при изменении х₂ на 0,5». Округлим шаг до 0.1.

3. Осуществим последовательное прибавление составляющих градиента к основному уровню. Получим серию опытов 5-9 крутого восхождения. Эти опыты часто называют мысленными.

Иногда имеет смысл оценить ожидаемые значения параметров оптимизации в мысленных опытах.

Проведем расчет для опытов 7 и 8 крутого восхождения. Для оценки параметра оптимизации использовано уравнение регрессии (4.1). Однако в табл. 4.5 приведены натуральные значения факторов, а в уравнении применяются кодированные значения. Поэтому необходимо натуральные значения перевести в кодированные по формуле

, (4.2)

где x_j  кодированное значение фактора; x_j  натуральное значение фактора; x_j0  натуральное значение основного уровня; J_j  интервал варьирования; j  номер фактора.

Согласно (4.2) для опытов 7 и 8 соответственно вычислим

x₁=-0,6; x₂=-1,5;

x₁=-0,8; x₂=-2,0.

Подставляя эти значения в уравнение регрессии (4.1), получаем y₇=95,95; y₈=98,6, где y_j  значение зависимой переменной, предсказанное с помощью уравнения регрессии.

Все выполненные расчеты по данному примеру сведены в табл. 4.5. Здесь x*  факторы в натуральных единицах; y*  среднее значение из двух параллельных опытов.