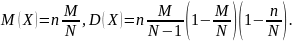6. Математич. Ожидание и дисперсия св, их св-ва. Среднее квадратическое отклонение.

Математическое ожидание дискретной СВ Х, принимающей конечное множество значений с законом распределения 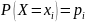, i=1,2,…, n, ,

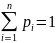наз. суммой произведений её значений на их соответствующие вер-ти: .

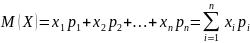Математическое ожидание дискретной СВ приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому всех ее возможных значений. Св-ва:

1. Значение математического ожидания СВ Х заключено между ее наименьшим и наибольшим значениями: 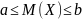, где a-наименьшее, b-наибольшее значение величин X.

2. Математическое ожидание постоянной величины равно этой постоянной: .

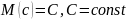3. Постоянный множитель можно вынести за знак математического ожидания: .

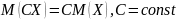4. Математическое ожидание суммы двух СВ равно сумме их математических ожиданий: 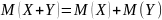. Это равенство распространяется и на n СВ .

5. Математическое ожидание разности двух СВ равно разности их математических ожиданий: .

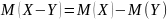6. Математическое ожидание произведения двух независимых СВ равно произведению математических ожиданий этих величин: 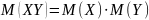. Это равенство распространяется и на n независимых СВ.

Дисперсией, или рассеянием, СВ называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: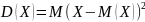 . Св-ва:

1. Дисперсия постоянной величины С равна нулю: 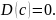Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

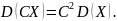
3. Дисперсия суммы или разности двух независимых случайных величин равна сумме дисперсий этих величин:

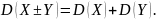
Для оценки рассеяния возможных значений СВ вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение. Средним квадратическим отклонением СВ Х называется квадратный корень из дисперсии: .

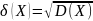7. Основные законы распределения дискретной случайной величины: биномиальное, Пуассона, гипергеометрическое.

Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли: 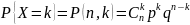, где p- параметр распределения 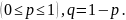Распределение загасит от двух параметров n и р.

На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из n испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в n опытах, имеет биноминальное распределение.

Числовые характеристики: 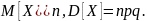Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона: , т.е. .

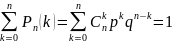Распределение Пуассона: В одинаковых условиях производится n независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие Ā с вероятностью q=1-p. Вероятность того, что при n испытаниях событие Ā появится k раз (и не появится п-k раз), определяется формулой Бернулли. Рассмотрим случай, когда n являются достаточно большим, а р – достаточно малым. Положим np=a, где а– некоторое число. Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой . Постоянную а=nр называют параметром распределения Пуассона. Распределение Пуассона является предельным случаем биномиального распределения, т. е. 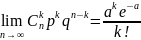. Можно показать, что математическое ожидание и дисперсия дискретной случайной величины, распределенной по закону Пуассона, равны числу а – параметру этого распределения. Иногда полезно использовать рекуррентную формулу 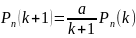, которая получается след. образом:

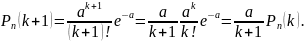
Дискретная случайная величина имеет гипергеометрическое распре-деление, если она принимает m значения с вероятностями 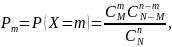где m=0,1,…, k; k=min (n, M);

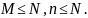
Вероятность 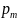является вероятностью выбора m объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных (без возврата) из совокупности N объектов, среди которых М объектов обладают заданным свойством.

Математическое ожидание и дисперсия случайной величины, имею-щей гипергеометрическое распределение с параметрами n, М, N: