
- •2. Теоремы сложения и умножения вер-й. Формула полной вер-ти. Ф-ла Байеса.
- •3. Повторные независимые испытания. Ф-ла Бернулли. Ф-ла Пуассона. Локальная и интегральная теоремы Муавра-Лапласа.
- •4. Дискретная случайная величина. Закон распределения дискретной случайной величины. Ряд распределения, полигон, ф-я распределения.
- •5. Непрерывная случайная величина. Ф-я распределения и её св-ва. Плотность вер-й и её св-ва.
- •6. Математич. Ожидание и дисперсия св, их св-ва. Среднее квадратическое отклонение.
- •7. Основные законы распределения дискретной случайной величины: биномиальное, Пуассона, гипергеометрическое.
- •8. Равномерное и показательное распределения непрерывной случайной величины.
- •9. Нормальное распределение: формулы плотности и ф-и распределения, числовые хар-ки, условия применимости. Правило трёх сигм.
- •10. Предельные теоремы. (пт)
1. Случ. события и их клас-я. Действия над событиями. Клас., геометр. и стат. опред. вер-ти случ. события. Св-ва вероятности. Опытом или испытанием называется всякое осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называют событием.
Событие называется случайным в данном опыте, если оно может произойти, а может и не произойти в этом опыте. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи.
Достоверным называется событие W, которое происходит в каждом опыте.
Невозможным называется событие Æ, которое в результате опыта произойти не может.
Несовместными называются события, которые в одном опыте не могут произойти одновременно.
Событием,
противоположным
к событию A наз. событие
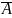 ,
кот. состоит из всех элементарных
событий не вход. в A.
,
кот. состоит из всех элементарных
событий не вход. в A.
Суммой (объединением) двух событий A и B называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Произведением (пересечением) двух событий A и B называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Классическое
опред. вер-ти:
Оно использ-ся, если кол-во исходов
опыта конечное множество и все эти
исходы равновероятны. Вер-ть события
равна отношению числа элементарных
событий, вход. в исходное событие к
числу всех возможных исходов. Вероятность
события определяется по формуле:
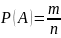 , где m - число равновозможных исходов,
приводящих к появлению события; n - число
элементарных равновозможных исходов
данного опыта.
, где m - число равновозможных исходов,
приводящих к появлению события; n - число
элементарных равновозможных исходов
данного опыта.
Геометрические вероятности: Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Пусть
на плоскости задача область G площади
Sg. В области G содержится область g
площади Sg. В область G наудачу брошена
точка. Будем считать, что брошенная
точка может попасть в некоторую часть
области G с вероятностью, пропорциональной
площади этой части и не зависящей от
ее формы и расположения. Пусть А –
попадание брошенной точки в область
g, тогда
геометрическая
вероятность
этого
события определяется формулой:
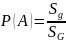 . Аналогично вводится понятие
геометрической вероятности при бросании
точки в пространственную область G
объема
. Аналогично вводится понятие
геометрической вероятности при бросании
точки в пространственную область G
объема
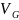 ,
содержащую область g объема Vg:
,
содержащую область g объема Vg:
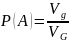 .
В
общем случае понятие геометрической
вероятности вводится следующим образом.
Если обозначить меру (длину, площадь,
объем) области через mes,
то вероятность попадания точки, брошенной
наудачу в область g
– часть области G,
равна
.
В
общем случае понятие геометрической
вероятности вводится следующим образом.
Если обозначить меру (длину, площадь,
объем) области через mes,
то вероятность попадания точки, брошенной
наудачу в область g
– часть области G,
равна
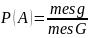 .
.
Статистические вероятности: Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность классического определения. Отмеченный недостаток может быть преодолен, в частности, введением геометрических вероятностей, и, конечно, использованием аксиоматической вероятности.
Слабая сторона классического определения состоит и в том, что часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными.
По этой причине наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение.
Относительной
частотой события называется отношение
числа ис-пытаний, в которых событие
появилось, к общему числу фактически
проведенных испытаний. Таким образом,
относительная частота события А
определяется формулой
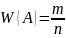 , где m – число появления события, n –
общее число испытаний.
, где m – число появления события, n –
общее число испытаний.
Св-ва вероятности: 1. Вероятность достоверного события равна единице.
Действительно,
если событие достоверно, то каждый
элементарный исход испытания
благоприятствует событию. В этом случае
m=n, следовательно
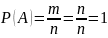 ;
;
2. Вероятность невозможного события равна нулю.
Действительно,
если событие невозможно, то ни один из
элементарных исходов испытания не
благоприятствует событию. В этом случае
m=0,
значит
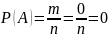 ;
;
3. Вероятность случайного события есть положительное число, за-ключенное между нулем и единицей.
Действительно,
случайному событию благоприятствует
лишь часть из общего числа элементарных
исходов испытания. В этом случае 0< m
< n, значит 0 < m/n < 1, т. е. 0 < Р(А) <
1. Итак, вероятность любого события
удовлетворяет двойному неравенству
0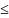 P(A)
1.
P(A)
1.
2. Теоремы сложения и умножения вер-й. Формула полной вер-ти. Ф-ла Байеса.
Сложение:
Если события
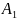 ,
,
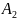 ,
…, Аn попарно несовместные, то вероятность
суммы этих событий равна сумме их
вероятностей, т. е.
,
…, Аn попарно несовместные, то вероятность
суммы этих событий равна сумме их
вероятностей, т. е.
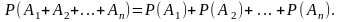 Вероятность
суммы двух совместных событий равна
сумме вероятностей этих событий без
вероятности их совместного появления.
Вероятность
суммы двух совместных событий равна
сумме вероятностей этих событий без
вероятности их совместного появления.
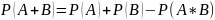
Сумма
вероятностей событий
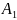 ,
,
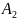 ,
… , An,
образующих полную группу событий, равна
единице:
,
… , An,
образующих полную группу событий, равна
единице:
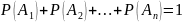 ;
;
Сумма
вероятностей противоположных событий
равна единице:
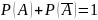 .
.
Умножение: Событие, сост. в том, что произошло событие В, когда известно, что произошло событие А обозначим В/А.
Соответствующая вер-ть P(B/A), наз. условной вероятностью события В при условии, что событие А произошло.
Можно показать, что для вер-ти произведения 2-х событий справедлива формула: P(A*B)=P(A)*P(B/A)=P(B)*P(A/B) (теорема умножения вероятностей),т.е. вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло.
Если Р (А/В) = Р (А), то говорят, что событие А не зависит от события В. Свойство независимости событий взаимное – если Р (А/В) = Р (А), то и
Р (В/А) = Р (В).
Для независимых событий А и В теорема умножения вероятностей за-писывается так: Р (АВ) = Р (А) Р (В).
Ф-ла
полной вер-ти: Пусть
событие А может осуществляться лишь
вместе с одним из событий ,
,
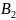 ,
…, Вn,
образующих полную группу событий. Тогда
вероятность появления события А ровна
сумме произведений вер-й событий
,
…, Вn,
образующих полную группу событий. Тогда
вероятность появления события А ровна
сумме произведений вер-й событий
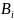 на
условную вер-ть события А, т.е.:
на
условную вер-ть события А, т.е.:
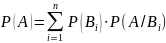 .
.
Здесь
P(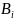 )-вер-ть
события
,
)-вер-ть
события
,
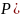 )-условная
вер-ть события А при этом событии.
)-условная
вер-ть события А при этом событии.
Так как заранее неизвестно, с каким из событий произойдет событие А, то события называются гипотезами.
Ф-ла
Байеса:
Пусть событие А, которое может наступить
только вместе с одним из событий
,
,
…, Вn,
образующих полную группу несовместных
событий, произошло в результате
какого-либо опыта. Тогда известные до
опыта вероятности P(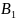 ),
P(
),
P(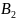 ),
…, P(Bn) с учетом появления события А
перевычисляются по формуле Байеса:
),
…, P(Bn) с учетом появления события А
перевычисляются по формуле Байеса:
)=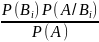 ,
i=1,2,…,n.
,
i=1,2,…,n.
Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
3. Повторные независимые испытания. Ф-ла Бернулли. Ф-ла Пуассона. Локальная и интегральная теоремы Муавра-Лапласа.
Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта.
Пусть
один тот же опыт проводятся n раз. В
каждом опыте некоторые события
,
,
…, Аr появляется с вероятностями
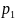 ,
,
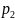 ,
…,
,
…,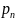 .
Будем рассматривать не результат
каждого конкретного опыта, а общее
число появлений событий
,
,
…, Аr . Рассмотрим случай с двумя
возможными исходами опытов, т.е. в
результате каждого опыта событие A
появляется с вероятностью р и не
появляется с вероятностью q=1-p. Вероятность
P(n,k) того, что в последовательности из
n опытов интересующее нас событие
произойдет ровно k раз (безразлично, в
какой последовательности), равна
(формула Бернулли)
.
Будем рассматривать не результат
каждого конкретного опыта, а общее
число появлений событий
,
,
…, Аr . Рассмотрим случай с двумя
возможными исходами опытов, т.е. в
результате каждого опыта событие A
появляется с вероятностью р и не
появляется с вероятностью q=1-p. Вероятность
P(n,k) того, что в последовательности из
n опытов интересующее нас событие
произойдет ровно k раз (безразлично, в
какой последовательности), равна
(формула Бернулли)
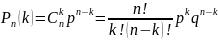 .
.
Ф-ла
Пуассона: При
больших n
малых, при малых вер-й используется
приближение к ф-ле Бернулли – ф-ла
Пуассона.
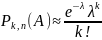 ,
,
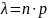 .
.
Локальная
теорема Муавра-Лапласа:
Если
вероятность появления события А в
каждом из n
(n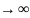 )
независимых испытаний равна одной и
той же постоянной р=const (0<р<1), то
вероятность
)
независимых испытаний равна одной и
той же постоянной р=const (0<р<1), то
вероятность
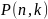 того, что во всех этих испытаниях событие
А появится ровно k раз, приближенно
вычисляется формулой:
того, что во всех этих испытаниях событие
А появится ровно k раз, приближенно
вычисляется формулой:
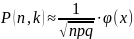 , где
, где
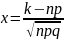 ,
,
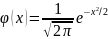 —кривая
Гаусса. Таблицы значений функции
—кривая
Гаусса. Таблицы значений функции
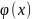 даны в приложениях к учебникам по теории
вероятностей.
даны в приложениях к учебникам по теории
вероятностей.
Интегральная
теорема Муавра-Лапласа:
Пусть вероятность появления события
А в каждом из n
(n→∞)
независимых испытаний равна одной и
той же постоянной р (0<р<1), то вероятность
того, что во всех этих испытаниях
событие А появится не менее
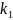 и не более
и не более
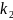 раз, приближенно вычисляется формулой:
раз, приближенно вычисляется формулой:
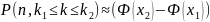 ,
где
,
где
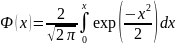 – ф-я
Лапласа,
– ф-я
Лапласа,
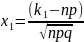 ,
,
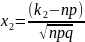
Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная - F(x)= F(-x).
