
- •7 Билет
- •1.Численное интегрирование временных рядов. Методы прямоугольников и трапеций. Погрешности.
- •2.Понятие о тренде в данных
- •8 Билет
- •Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных
- •2.Частное определение: определение скользящего среднего
- •9 Билет
- •1. Дифференциальные уравнения первого и второго порядков: основные определения и способы решений. Общее и частное решения.
- •Частное определение: суть интерполяции данных
- •Метод Эйлера решения обыкновенных дифференциальных уравнений.
- •Частное определение: суть аппроксимации данных
- •11.Билет
- •1. Метод Рунге-Кутта.Решения обыкновенных дифференциальных уравнений.
- •2. Частное определение: определение невязки
- •13. Билет
- •Частное определение: определение характерного масштаба процесса.
- •14. Билет
- •1. Задачи Коши для обыкновенного дифференциального уравнения. Физический смысл начальных условий. Пример на схеме метода Эйлера
- •2.Частное определение: суть метода наименьших квадратов
- •1. Дифференциальные уравнения в частных производных. Моделирование диффузии.
- •2. Частное определение:
- •3. Лабораторная работа: Гармонический анализ временных рядов.
- •1. Сетевые графики и метод календарного планирования.
- •2. Частное определение:
- •3. Лабораторная работа: Уравнение линейной регрессии. Метод наименьших квадратов.
Экзаменационный билет № 1
Переменные величины и функции при изучении природных систем. Методы визуализации натурных данных. Графики изменчивости переменных вели Переменной называется величина, принимающая различные числовые значения. Областью изменения переменной называется совокупность всех принимаемых ею числовых значений. Она может состоять из одного или нескольких интервалов и из отдельных точек. Взаимосвязанное изменение переменных называется функциональной зависимостью. При изучении функциональной зависимости между двумя переменными полагают, что одна из них является независимой переменной, которой можно придавать произвольные значения из области ее изменения, а другая — зависимой от нее. Независимая переменная называется аргументом, а зависимая — функцией. Н. И. Лобачевскому принадлежит следующее определение понятия функции: переменная у называется функцией переменной х, если каждому значению х, из области ее изменения, соответствует определенное значение у. Для сокращения записей употребляется символическое обозначение функций: y = f(x), S = op(/), u = F(v),... Если функция от х обозначена символом Р (*), то Р (а) обозначает частнсе значение этой функции при х — а. — 7 — Так, если Р (х) --- х-4-2л:— 5, то Р (3) = З2 + 2 • 3 - 5 = 10; Р (0) = — 5; Р (я) - я3 4 2а - 5. Основными элементарными функциями называются: 1) степенная функция у = х"\ 2) показательная функция у = ах, а>0; 3) логарифмическая функция у = \ogax, я>0; 4) тригонометрические функции у = sin х, у — cosx, у—Л gx, у = ctgx, y = sccx, у cosec, х\ 5) обратные тригонометрические функции у — arc sin х, у —= arc cos х, у = arctgx, y=arcctgx. Функции, заданные одной формулой посредством конечного числа арифметических действий и операций, определяемых основными элементарными функциями, называются элементарными. Например: г/ = 5л'3 sin 2х; у= . Все остальные функции называются н е э л е м е н т а р н ы м и. Например, неэлементарной является функция, определяемая несколькими различными формулами для различных интервалов изменения аргумента: | х3 при ж;0 ^ — \ х + 2 при х> 0. Функция f(x), обладающая свойством f(x) = f(— х), называется четной, например x2,cosx, а обладающая спойством f(x)--~ —называется нечетной, например х'л, sin х. Многие функции не являются ни четными, ни нечетными, например (Г, Ух. Визуализация в общем смысле — метод представления информации в виде оптического изображения (например, в виде рисунков и фотографий, графиков, диаграмм, структурных схем, таблиц, карт и т. д. чин. Графики предназначены прежде всего для иллюстрирования математических понятий, функциональных зависимостей или связей между объектами (теория графов). Графики Показывают зависимость данных друг от друга. Строятся по осям X и Y, хотя могут быть и трехмерными. Линейный график (line chart, area chart). Наиболее распространенный случай. Объединяет линией набор точек, соответствующих значениям по осям. Например, ежедневная посещаемость сайта за месяц. Может показывать сразу несколько наборов данных — например, статистику просмотров для 3 наиболее популярных страниц. Диаграммы сравнения Показывают соотношения набора данных. Во многих случаях строятся вокруг осей, хотя и необязательно.
2. Частное определение: Дифференциальное уравнение как модель изменчивости процессов. Дифференциальное уравнение - неизвестная величина стоит под знаком производной (y(x))`
|
||||||||||||||||
Экзаменационный билет № 2
Пусть известные значения некоторой функции f образуют следующую таблицу:
При этом требуется получить значение функции f для такого значения аргумента х, которое входит в отрезок [x0;xn], но не совпадает ни с одним из значений xi (i=0,1,…,n). Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках xi(i=0, 1, 2, …, n), т.е.F(x0)=y0, F(x1)=y1, …, F(xn)=yn В этом случае нахождение приближенной функции называют
интерполяцией,
а точки x0,
x1,
…, xn – узлами
интерполяции.
Геометрически это означает, что нужно
найти кривую y=F(x) некоторого
определенного типа, проходящую через
заданную систему
точек Mi(xi,yi) (i=0,1,2,…,n) (рис.
1). В случае, если x
З Когда искомое значение y(x) вычисляется в точке x, которая находится между каких-либо из узлов xi, говорят об интерполяции, а когда точка x лежит вне границ интервала, включающего все xi - об экстраполяции функции y(x).
Линейная
интерполяция состоит
в том, что заданные точки
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (1) и найти приближенное значение функции в этой точке.
Квадратичная
интерполяция. В
качестве интерполяционной функции
на отрезке
Уравнение
квадратного трехчлена
содержит
три неизвестных коэффициента ai, bi, ci,
для определения которых необходимы
три уравнения. Ими служат условия
прохождения параболы (2) через три
точки
При
вычислении приближенного значения
функции с помощью квадратичной
интерполяции вместо формулы (1) нужно
использовать (2) с учетом решения
системы линейных уравнений (3).
Интерполяция для любой точки Экстраполяция (от экстра… и лат. polio — приглаживаю, выправляю, изменяю) в математике — особый тип аппроксимации (приближения), при котором функция аппроксимируется не между заданными значениями, а вне заданного интервала. Экстраполяция — приближённое определение значений функции f(x) в точках х, лежащих вне отрезка [х0, хn], по её значениям в точках х0< x1 < . .< xn 2. Частное определение: Определение фильтрации данных. фильтрация данных — это отсеивание «лишних» данных, в которых нет необходимости для повышения достоверности и адекватности Метод фильтрации данных Сущность фильтрации состоит в том, что решение принимается на основании сопоставления входящих данных с комплексом заранее сформулированных независимых признаков, каждому из которых приписывается вес (важность). Этот комплекс и является фильтром. Фильтр есть обоснованная опытом и теорией система смысловых и логических между свойствами ситуации, объекта, события и их внешними проявлениями, признаками. Т.е. если информация удовлетворяет фильтру, она считается достоверной, если не удовлетворяет - недостоверной. Признаки, включенные в фильтр, называются параметрами фильтра. Например: фильтр оценки возможности поражения чего-либо из оружия состоит из следующих признаков: оружие должно быть функционально готово к выстрелу, заряжено, наведено на цель и т.д. Если поступает сообщение о готовящемся поражении из данного оружия одновременно с сообщением о том, что оно не заряжено, то такое сообщение фильтр не походит и считается ложным. Из поступающего сообщения выделяются только те данные, которые имеют отношение к признакам фильтрации. Эти данные классифицируются. Оценивается их достоверность. Затем принимается отдельное решение по каждому из параметров фильтра: есть соответствующий признак или нет. Информационное решение принимается на основании подтвержденных признаков путем сравнения их суммарного веса с порогом. Принципиальное отличие метода фильтрации от метода сопоставления данных состоит в том, что в методе фильтрации содержание возможных решений формулируется заранее, анализ входной информации происходит по готовым признакам, а в методе сопоставления данных признаки, подлежащие оценке, выявляются в процессе анализа информации. Основное преимущество метода фильтрации в его относительной простоте (нет сложной и неоднозначной процедуры определения сопоставимых признаков в разных сообщениях). Недостатком является то, что сведения, не относящиеся к параметрам фильтра, просто не используются. Это порождает пренебрежение новой, непривычной информацией и это необходимо учитывать. |
||||||||||||||||
Экзаменационный билет № 3
1. Методы аппроксимации табличных данных. Невязки. Метод наименьших квадратов. |
||||||||||||||||
Е 1. Аппроксимировать опытные данные интерполяционным многочленом степени n, который проходит через все узловые точки. 2. Аппроксимировать опытные данные некоторой функцией, которая в некотором смысле проходит близко около каждого из узлов (метод наименьших квадратов). Первый способ гарантирует точность лишь в небольшом интервале при небольшом количестве точек. При этом значения функции в узлах должны быть заданы с большой точностью. В результате же эксперимента неизбежны погрешности. Реальная наблюдаемая величина всегда зависит от многих факторов и это вызывает случайные колебания изучаемой функции. Увеличивая число узлов интерполяции, мы воспроизводим случайные колебания, а не закономерные изменения.
Н
Для
табличных данных, полученных в
результате эксперимента, требуется
отыскать такую функцию , чтобы
сумма квадратов уклонений была
минимальной.
Невязка —
это ошибка (погрешность)
в результате вычислений. Пусть мы
хотим найти такое x,
что значение функции: Невязка аппроксимации функции
Для
аппроксимации fa решения f уравнения
Метод наименьших квадратов Метод наименьших квадратов (МНК) - Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции. Задача приближения функции f: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.
Р (1) Пусть F(xi, a, b, c) = yi, i=1, 2, ..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:
Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:
П
(3)
Решив эту систему получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (3).
З 2. Частное определение: Определение гармонического анализа. Гармони́ческий ана́лиз (или Фурье́-ана́лиз) — раздел математики, в котором изучаются свойства функций с помощью представления их в виде рядов или интегралов Фурье. Также метод решения задач с помощью представления функций в виде рядов или интегралов Фурье. Метод анализа был основан на так называемых рядах Фурье. Говоря языком математики, ряд Фурье — это метод представления функции суммой синусоид и косинусоид, поэтому анализ Фурье был известен также под названием «гармонический анализ». Гармонический анализ – это раздел математики, связанный с разложением колебаний на гармонические колебания (колебания, при которых физическая величина изменяется с течением времени по закону синуса или косинуса). В самой общей формулировке можно сказать, что преобразования Фурье применяется в тех областях, где изучаются колебательные процессы. Поэтому ясно, что сфера его применения очень широка. С помощью анализа Фурье специалисты из Национального управления по аэронавтике и исследованию космического пространства повышают чёткость изображений небесных тел, сфотографированных с космических аппаратов. Автоматические межпланетные станции и искусственные спутники Земли передают информацию на Землю в виде последовательностей радиоимпульсов. Компьютеры обрабатывают эти импульсы с помощью методов Фурье. При этом компьютер модулирует отдельные компоненты каждого преобразования, чтобы чётче выделить одни свойства и устранить другие, аналогично тому, как с помощью преобразования Фурье устраняется шум из сигнала музыкальной записи. В конечном итоге изменённые таким образом данные опять преобразуются к исходной форме, и тем самым восстанавливается изображение. При помощи описанного процесса можно резче сфокусировать изображение, отфильтровать туманный фон и отрегулировать контрастность.
Экзаменационный билет № 4
1. Поиск простейших эмпирических зависимостей при помощи среднеквадратичного приближения. Невязки. Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей
Необходимо найти функцию заданного вида: y=F(x), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn.
Идея состоит в том, чтобы максимально приблизить данные из таблицы (на графике это звездочки) к прямой или любой другой функции, которая отобразит распределение этих точек наиболее близко. Невязки. На графике это разница между точкой на прямой и «звездочкой» (получается опусканием перпендикуляра из звездочки к прямой). Линейная функция (линейная регрессия).
Предположим,
что связь между x и y линейна и искомую
приближающую функцию будем искать в
виде:
Найдем
частные производные по параметрам:
Подставим полученные соотношения в систему вида :
Далее имеем:
или, деля каждое уравнение на n:
Введем обозначения:
Тогда последняя система будет иметь вид:
где xi, yi - значения из таблицы. Решив систему, получим значения параметров a и b , а следовательно, и конкретный вид линейной функции. Невязка – разница между эмпирическими значениями и значениями аппроксимирующих линий; или разница между наблюденными аппроксимирующих функций. Поиск простейших эмпирических зависимостей необходим чтобы упорядочить значения системы, заменить одну систему координат на другую. Z = axm lnz = lna + m lnx соответственно Y = AX + B – линейная зависимость, а х = lnx и у = lnz – логарифмич замена. Переходим к билогарифмированию:
В естествознании часто используется метод наименьших квадратов - метод оценивания параметров приближающей функции, кот сводит к min сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
2. Частное определение: определение сглаживания данных Сглаживание предполагает использование набора значений y (и возможно x) и возвращение нового набора значений y, который является более гладким, чем исходный набор. В отличие от регрессии и интерполяции, обсужденных ранее, сглаживание приводит к новому набору значений y, а не к функции, которая может оценивать значения между заданными точками данных. Таким образом, если Вас интересуют значения y между заданными значениями y, необходимо использовать интерполяцию или регрессию. Так как каждый элемент в векторе должен иметь значение, Mathcad присваивает значение 0 любым элементам, которые явно не определены. Функция medsmooth — наиболее устойчивая из трех, так как в меньшей степени подвержена влиянию зашумленных данных. Эта функция использует сглаживание с помощью скользящей медианы, вычисляет остатки, сглаживает остатки тем же самым образом и суммирует эти два сглаженных вектора вместе. Более подробно:
Обратите внимание, что medsmooth будет оставлять первые и последние (n-1)/2 точки неизменяемыми. На практике длина окна сглаживания n должна быть мала по сравнению с длиной набора данных. Функция ksmooth использует гауссово ядро, чтобы вычислить локально взвешенные средние значения исходного вектора vy. Это сглаживание наиболее полезно, когда данные взяты в точках, отделяемых друг от друга интервалами приблизительно равной ширины. Если длина интервалов существенно изменяется, следует использовать адаптивное сглаживание подобное supsmooth. Для каждого vyi в n-мерном векторе vy функция ksmooth возвращает новый vy'i, даваемый формулой
где
и b — параметр сглаживания. Его величина обычно устанавливается в несколько раз больше величины интервала между точками данных на оси x и определяется тем, насколько большое окно желательно использовать при сглаживании. Функция supsmooth использует симметричную линейную процедуру сглаживания методом наименьших квадратов по правилу k-ближайших соседей, чтобы выполнить локальную линейную аппроксимацию исходных данных. В отличие от ksmooth, который использует фиксированную ширину полосы сглаживания для всех исходных данных, supsmooth адаптивно выбирает различную ширину полосы сглаживания для различных частей данных.
|
||||||||||||||||
Экзаменационный билет № 5
Общее представление о рядах Фурье. Гармонический анализ временных рядов 1.
Многие
природные процессы являются
периодическими, т.е. воспроизводятся
в прежнем виде через определенный
промежуток времени Т (смена времен
года, смена дня и ночи, продолжительность
светового дня и т.д.). С точки зрения
математики, различные величины,
связанные с рассматриваемыми
периодическими процессами, по истечение
периода Т возвращаются к своим прежним
значениям и являются периодическими
функциями от времени t:
Гармонический анализ – это процесс разложения периодической функции в ряд Фурье (на гармоники). Гармоника (гармонические составляющие функции f(t)) – отдельные синусоидальные величины, входящие в состав тригонометрического ряда. Ибо периодическая функция f(t) периода Т (при этом составляющие синусоидальные величины разных частот) может быть представлена в виде суммы конечного или бесконечного множества синусоид. Интерпретация полученных результатов: с помощью гармонического анализа можно выделить низко-, средне- и высокочастотные колебания, а также оценить вклад отдельных гармоник в исследуемый процесс. Задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично. По этим коэффициентам можно судить о вкладе отдельных гармоник: если k≈0, то вклад гармоник минимальный, а если k≈1, то это основные гармоники. По ним можно составлять гипотезы и процессооформирующих явлениях.
Пусть
ф-ия f(x) –
периодическая с периодом 2π: f(x+2π)=f(x).
Основная задача гармонического анализа
– представить ф-цию f(x)
в виде ряда:
Полагая
что
Ряд Фурье и гармонический анализ позволяют выполнить фильтрацию временного ряда. Напр.: *Если обнулить n-компонент (с низкими частотами), то это высокочастотная фильтрация; *Если удалить все компоненты с какой-то высокой частотой, то это будет низкочастотная фильтрация; *Обнулив компонент со значениями частот «от и до» - полосовая фильтрация. Иногда фильтрация с пропусканием высоких частот производится путем вычитания сглаженных величин из данного ряда, в рез-те в ряду остаются только высокие частоты. 1)Фильтрация низких и высоких частот, в рез-те чего в ряду остаются средние частоты. Иногда эти частоты получаются путем дополнительного сглаживания ряда данных, полученных путем вычитания первоначального сглаживания величин из экспериментального ряда. 2)Существуют фильтры позволяющие усилить высокие частоты. Этим достигается ликвидация эффекта предыдущего сглаживания (процесс «обратного сглаживания»). Простейшими фильтрами являются скользящая средняя и взвешенная скользящая средняя.
2. Частное определение: суть аппроксимации данных Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся функцию, называемой аппроксмирующей, а действие замены аппроксимацией. Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей
Необходимо найти функцию заданного вида: y=F(x), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn. По таблице строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции. Рассмотрим рисунок:
На рисунке изображены три ситуации: 1) график а - взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий. 2) график b - реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами. 3) график с - явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
|
||||||||||||||||
Экзаменационный билет № 6 1. Сглаживание и фильтрация временных рядов. Определения и основные алгоритмы. особенности экспериментальных временных рядов заключаются в следующем: 1. На практике обычно приходится анализировать временные ряды с достаточно большим количеством отсчетов (не менее нескольких десятков).
2. Отсчеты,
как правило, производятся через равные
промежутки времени (равноотстоящие
узлы зависимости при
3. Зависимость 4. Приближающую функцию, аппроксимирующую временной ряд по всей его длине, как правило, невозможно описать аналитически.
Особенности
временных рядов хорошо поясняет
простейший пример. Проведем однофакторный
эксперимент, регистрируя значения
входных В теории обработки временных рядов существует множество способов их сглаживания: фильтрация с использованием преобразования Фурье, кусочная аппроксимация многочленами и др… Мы рассмотрим два простейших, но принципиально разных вида сглаживания, которые, в какой-то мере, обобщают особенности этой процедуры: 1)метод скользящего среднего; 2)медианное сглаживание.
Рассмотрим
две случайные зависимости, показанные
на рис.3.7. Зависимости имеют одинаковую
регулярную составляющую
Рис.3.8 Целью сглаживания является получение плавной зависимости . Метод скользящего среднего предполагает выбор окна усреднения , и для каждого рассчитывается среднее значения на этом интервале:
Этот метод позволяет сгладить случайную составляющую зависимости, то есть избавиться от высокочастотных флуктуаций. При этом фильтрация высоких частот зависит от длины интервала усреднения .
Если
применить метод скользящего среднего
к зависимости рис.3.7,б, имеющей
значительные, но редкие выбросы, то
полученная сглаженная зависимость При наличии редких выбросов (рис.3.7,б) удобнее применять метод медианного сглаживания, в котором на «скользящем» интервале для получения используется не среднее значение функции, а медиана.
Пусть
на интервал
попало
четыре значения временного ряда
,
и одно из значений
сильно
отличается от других (см. рис.3.9, точка
3). Построение медианы по Необходимо иметь в виду, что зависимости и , полученные методом скользящего среднего и методом медианного сглаживания отличаются. Их отличие возрастает при увеличении частоты возникновения аномальных выбросов. Если выбросы возникают в анализируемой временной зависимости достаточно часто, то они могут рассматриваться как неотъемлемая характеристикафлуктуационной составляющей и их устранение при сглаживании искажает адекватное описание случайного ряда. Для оценки частоты выбросов могут использоваться разные критерии, например, средняя частота возникновения выбросов на выбранном временном интервале или отношение их общего количества к длине временного ряда. Кроме того, возникает вопрос: флуктуации какой амплитуды считать выбросами? Более подробно выбросы случайных процессов будут рассмотрены в пятой главе.
2. Частное определение: определение математического маятника
Математи́ческий
ма́ятник — гармонический
осциллятор, представляющий собой
механическую систему, состоящую из
материальной точки, подвешенной на
невесомой нерастяжимой нити или на
невесомом стержне в поле тяжести.
Уравнение математического маятника
без затухания (т.к. справа 0):
Общее
решение математического маятника:
Приближённое решение математического маятника: Условие:
Пусть
Получаем
систему:
Решение системы диф. уравнений методом Рунге-Кутта – простейшее решение математического маятника: Для решения надо найти 8 коэффициентов (2 набора k и m):
Для коэффициентов m в левой части k заменяем на m и SY на SZ, а в правой - F на G. Составляем систему решений:
Основная идея численного метода решения дифференциального уравнения второго порядка-переход от див. уравнения n-го порядка к системе уравнений 1-го порядка:
Пр.:
пусть
Пр.:
Ещё
одна замена:
|
7 Билет
1.Численное интегрирование временных рядов. Методы прямоугольников и трапеций. Погрешности.
З начение
определенного интеграла численно равно
площади криволинейной трапеции,
ограниченной графиком функции y=f(x),
осью абсцисс и прямыми х=а,
х=b.
Находя приближенно площадь криволинейной
трапеции, мы получаем значение интеграла.
Формально процедура численного
интегрирования заключается в том, что
отрезок [а, b]
разбивается на n
частичных отрезков, а затем подинтегральная
функция заменяется на нем легко
интегрируемой функцией, по определенной
зависимости интерполирующей значения
подинтегральной функции в точках
разбиения.
начение
определенного интеграла численно равно
площади криволинейной трапеции,
ограниченной графиком функции y=f(x),
осью абсцисс и прямыми х=а,
х=b.
Находя приближенно площадь криволинейной
трапеции, мы получаем значение интеграла.
Формально процедура численного
интегрирования заключается в том, что
отрезок [а, b]
разбивается на n
частичных отрезков, а затем подинтегральная
функция заменяется на нем легко
интегрируемой функцией, по определенной
зависимости интерполирующей значения
подинтегральной функции в точках
разбиения.
 -
площадь левого прямоугольника
-
площадь левого прямоугольника
 -
площадь правого прямоугольника
-
площадь правого прямоугольника
Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Заметно меньшую погрешность дает метод трапеций.
Метод прямоугольников
Итак,
функция у=f(x)
интегрируема на сегменте [a,b]
и требуется вычислить ее интеграл
 .
Составим интегральную сумму для f(x)
на сегменте [a,b]
. Для этого разобьем сегмент [a,b]
на n
равных между собой частей с помощью
точек: x1,
x2,
… , xk,
… , xn-1.
.
Составим интегральную сумму для f(x)
на сегменте [a,b]
. Для этого разобьем сегмент [a,b]
на n
равных между собой частей с помощью
точек: x1,
x2,
… , xk,
… , xn-1.
Если
длину каждой части мы обозначим через
х,
так что
 ,
то для каждой точки xiбудем
иметь:
,
то для каждой точки xiбудем
иметь:
 (i=0,
1, 2, …, n).
(i=0,
1, 2, …, n).
Обозначим
теперь через yi
значение подынтегральной функции
f(x)
при
 ,
то есть положим
,
то есть положим
 (i=0,
1, …, n).
(i=0,
1, …, n).

 -
формула левых прямоугольников или
-
формула левых прямоугольников или
 -
формула правых прямоугольников.
-
формула правых прямоугольников.
Метод трапеций
Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы (3а) и (3б). Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения.
Простейшая из таких формул получается как среднее арифметическое правых частей формул (1) и (1'):
 (4)
(4)
Легко
усмотреть геометрический смысл этой
формулы. Если на каждом отрезке разбиения
дугу графика подинтегральной функции
y=f(x) заменить стягивающей ее хордой
(линейная интерполяция), то мы получим
трапецию, площадь которой равна ![]() и
следовательно, формула (4) представляет
собой площадь фигуры, состоящей из таких
трапеций (рис.10) . Из геометрических
соображений понятно, что площадь такой
фигуры будет, вообще говоря, более точно
выражать площадь криволинейной трапеции,
нежели площадь ступенчатой фигуры,
рассматриваемая в методе прямоугольников.
и
следовательно, формула (4) представляет
собой площадь фигуры, состоящей из таких
трапеций (рис.10) . Из геометрических
соображений понятно, что площадь такой
фигуры будет, вообще говоря, более точно
выражать площадь криволинейной трапеции,
нежели площадь ступенчатой фигуры,
рассматриваемая в методе прямоугольников.

Приведя в формуле (4) подобные члены, окончательно получим
 (5)
(5)
Формулу (5) называют формулой трапеций.
Формулой трапеций часто пользуются для практических вычислений.
Погрешности
Что касается оценки погрешности Rn, возникающей при замене левой части (5) правой, то доказывается, что абсолютная величина ее удовлетворяет неравенству:
 (6)
(6)
где М2 – максимум модуля второй производной подинтегральной функции на отрезке [a,b], т.е.
![]() .
.
Следовательно, Rn убывает
при ![]() по
крайней мере так же быстро, как
по
крайней мере так же быстро, как ![]() .
.
Абсолютная
погрешность Rn будет
меньше наперед заданного числа ![]() > 0,
если взять
> 0,
если взять  .
.

 адача
интерполяции функции одной переменной
состоит в замене дискретной зависимости
y(xi),
т.е. N пар чисел (xi,yi),
или, по-другому, узлов, некоторой
непрерывной функцией y(x). При этом
основным условием является то, что
функция y(x) должна проходить через
точки (xi,yi),
т. е. y(xi)=yi ,i=1...N,
а также возможность вычислить значение
y(x) в любой точке, находящейся между
узлов.
адача
интерполяции функции одной переменной
состоит в замене дискретной зависимости
y(xi),
т.е. N пар чисел (xi,yi),
или, по-другому, узлов, некоторой
непрерывной функцией y(x). При этом
основным условием является то, что
функция y(x) должна проходить через
точки (xi,yi),
т. е. y(xi)=yi ,i=1...N,
а также возможность вычислить значение
y(x) в любой точке, находящейся между
узлов.
 (3)
(3) сли
в результате эксперимента или
практической деятельности получено n +1
опытных данных (xi, yi); i =
0, 1, …, n ,
которые занесены в таблицу, и по ним
построен график. Аппроксимацияопытных
данных состоит в нахождении аналитического
выражения некоторой функции F(x)
(аппроксимирующей кривой), которая
приближала бы полученную табличную
функцию. Существует два метода
аппроксимации:
сли
в результате эксперимента или
практической деятельности получено n +1
опытных данных (xi, yi); i =
0, 1, …, n ,
которые занесены в таблицу, и по ним
построен график. Аппроксимацияопытных
данных состоит в нахождении аналитического
выражения некоторой функции F(x)
(аппроксимирующей кривой), которая
приближала бы полученную табличную
функцию. Существует два метода
аппроксимации: а
практике, часто используют другой
метод аппроксимации опытных данных.
Аппроксимирующую кривую проводят
так, чтобы она сгладила все случайные
помехи табличной функции. При
аппроксимации кривую F(x)
проводят так, чтобы все ее отклонения
от табличной функции (уклонения) были
бы наименьшими. Пусть
а
практике, часто используют другой
метод аппроксимации опытных данных.
Аппроксимирующую кривую проводят
так, чтобы она сгладила все случайные
помехи табличной функции. При
аппроксимации кривую F(x)
проводят так, чтобы все ее отклонения
от табличной функции (уклонения) были
бы наименьшими. Пусть ассмотрим
метод нахождения приближающей функции
в общем виде на примере аппроксимирующей
функции с тремя параметрами:
ассмотрим
метод нахождения приближающей функции
в общем виде на примере аппроксимирующей
функции с тремя параметрами:
 олучаем
систему для определения неизвестных
параметров a, b,
c.
олучаем
систему для определения неизвестных
параметров a, b,
c.
 начения
найденной функции F(x, a, b, c) в точках
х1, x2, ..., xn, будут
отличаться от табличных значений y1,
y2, ..., yn. Значения разностей
yi-F(xi,a, b, c)=i
(i=1, 2, ..., n) называются отклонениями
измеренных значений y от вычисленных
по формуле (1). Для найденной эмпирической
формулы y=F(x)
в соответствии с исходной таблицей
можно, следовательно найти сумму
квадратов отклонений ,
которая в соответствии с методом
наименьших квадратов для заданного
вида приближающей функции (и найденных
значений параметров) должна быть
наименьшей. Из двух разных приближений
одной и той же табличной функции,
следуя методу наименьших квадратов,
лучшим нужно считать то, для которого
сумма (2) имеет наименьшее значение.
начения
найденной функции F(x, a, b, c) в точках
х1, x2, ..., xn, будут
отличаться от табличных значений y1,
y2, ..., yn. Значения разностей
yi-F(xi,a, b, c)=i
(i=1, 2, ..., n) называются отклонениями
измеренных значений y от вычисленных
по формуле (1). Для найденной эмпирической
формулы y=F(x)
в соответствии с исходной таблицей
можно, следовательно найти сумму
квадратов отклонений ,
которая в соответствии с методом
наименьших квадратов для заданного
вида приближающей функции (и найденных
значений параметров) должна быть
наименьшей. Из двух разных приближений
одной и той же табличной функции,
следуя методу наименьших квадратов,
лучшим нужно считать то, для которого
сумма (2) имеет наименьшее значение.







 ,
где коэф. ряда определяется по формулам
Эйлера-Фурье:
,
где коэф. ряда определяется по формулам
Эйлера-Фурье:
 ;
;
 ;
;

 ,
,
 ,
,
 ряд можно представить в виде:
ряд можно представить в виде:
 ,
где
,
где
 - амплитуда гармоники,
- амплитуда гармоники,
 - фаза
- фаза
 )
) заведомо
немонотонна и, чаще всего, ограничена.
Поэтому, если выбрать конечный
интервал
заведомо
немонотонна и, чаще всего, ограничена.
Поэтому, если выбрать конечный
интервал  ,
то для любого
,
то для любого  с
увеличением длины временного ряда
количество значений
с
увеличением длины временного ряда
количество значений ,
попадающих в интервал
,
попадающих в интервал  будет
увеличиваться.
будет
увеличиваться. и
выходных
параметров
одновременно, в моменты времени
и
выходных
параметров
одновременно, в моменты времени  ,
через равные промежутки
.
Тогда функциональная зависимость
,
через равные промежутки
.
Тогда функциональная зависимость  ,
описывающая результаты эксперимента,
задается параметрически, через два
временных ряда
,
,
описывающая результаты эксперимента,
задается параметрически, через два
временных ряда
,  .
. ,
а случайные составляющие зависимостей
отличаются: зависимость рис.3.7,б кроме
мелких случайных флуктуаций имеет
редкие выбросы достаточно большой
амплитуды.
,
а случайные составляющие зависимостей
отличаются: зависимость рис.3.7,б кроме
мелких случайных флуктуаций имеет
редкие выбросы достаточно большой
амплитуды.
 . (3.3.1)
. (3.3.1) резко
отличается от
резко
отличается от  .
Выбросы, за счет их высокой амплитуды,
сильно влияют на среднее значение,
как только попадают в интервал
усреднения, то есть каждый выброс
искажает
.
Выбросы, за счет их высокой амплитуды,
сильно влияют на среднее значение,
как только попадают в интервал
усреднения, то есть каждый выброс
искажает  на
интервале длиной
.
В случае, когда выбросы имеют редкий
и случайный характер, для выделения
регулярной составляющей метод
скользящего среднего неприемлем.
на
интервале длиной
.
В случае, когда выбросы имеют редкий
и случайный характер, для выделения
регулярной составляющей метод
скользящего среднего неприемлем.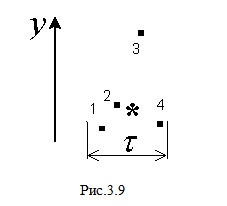
 предполагает,
что медианный центр, обозначенный
звездочкой, будет находиться в области
точек 1, 2 и 4, так как выше и ниже его
должны находиться по две точки. Таким
образом, выброс в точке 3 на сглаженной
зависимости будет устранен.
предполагает,
что медианный центр, обозначенный
звездочкой, будет находиться в области
точек 1, 2 и 4, так как выше и ниже его
должны находиться по две точки. Таким
образом, выброс в точке 3 на сглаженной
зависимости будет устранен. ,
где w-собственная частота
гармонического осциллятора. Уравнение
вида
,
где w-собственная частота
гармонического осциллятора. Уравнение
вида
 - математический маятник с трением,
где k – коэф. трения.
Уравнение вида
- математический маятник с трением,
где k – коэф. трения.
Уравнение вида
 - с вынуждающей функцией.
- с вынуждающей функцией.
 ,
с1, с2 – постоянные
интегрирования. Пр.: При
,
с1, с2 – постоянные
интегрирования. Пр.: При
 ,
->
,
->
 и
и
 .
.
 ,
где
,
где
 -трение
маятника о воздух, или толчок маятника
рукой. Пусть
-трение
маятника о воздух, или толчок маятника
рукой. Пусть
 ,
тогда
,
тогда
 .
.



 .
Обозначим
.
Обозначим
 ,
тогда
,
тогда
 .
Подставим:
.
Подставим:

 Обозначим:
Обозначим:
 Подставим
Подставим

 Получаем:
Получаем: