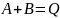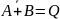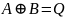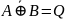4.7. Логический элемент или исключающее-не
Логический
элемент ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ называют
также элементом отрицания ИЛИ ИСКЛЮЧАЮЩЕГО.
Это говорит о том, что для реализации
функции ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ выход элемента
ИЛИ ИСКЛЮЧАЮЩЕГО должен быть инвертирован,
т.е.
.
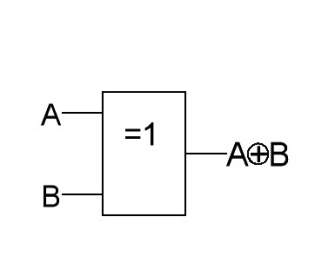
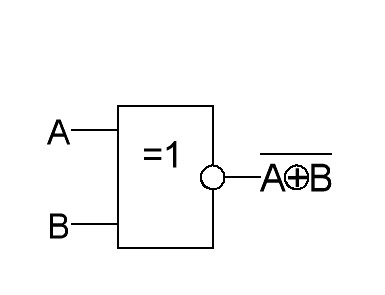
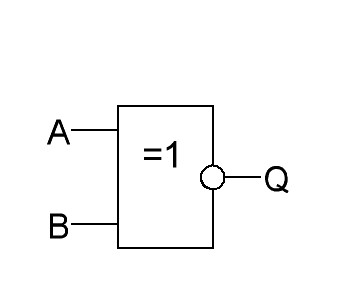
Условное изображение логического
элемента ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ показано
на рис.26,а.
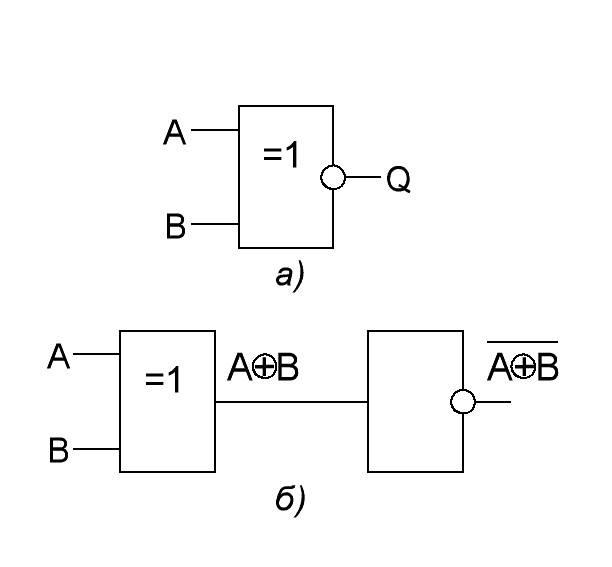
Рис.26. Логический элемент 2-ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ: а–условное изображение элемента 2-ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ; б–логическое выражение для выхода логического элемента 2-ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ
На рис.26,б раздельно показаны логический элемент 2-ИЛИ ИСКЛЮЧАЮЩЕЕ и инвертор, совместное использование которых обеспечивает логическую функцию 2-ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ.
В табл.10 приведена таблица истинности для логического элемента 2-ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ.
Таблица 10
В |
А |
Q |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
4.8. Универсальный характер логического элемента и-не (теорема Моргана)
До сих пор мы изучали основные логические элементы, используемые в любых цифровых электронных схемах. Мы познакомились с семью различными логическими элементами: ИЛИ, И, ИЛИ ИСКЛЮЧАЮЩЕЕ, ИЛИ-НЕ, И-НЕ, ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ и инвертор. Среди интегральных микросхем (ИС), имеющихся в широкой продаже, можно приобрести схемы, реализующие любую из приведенных семи основных логических функций.
В рекламной и справочной литературе логические элементы И-НЕ представлены более широко по сравнению со многими другими типами логических элементов. Поэтому покажем, каким образом можно реализовать все другие логические функции на основе универсального логического элемента И-НЕ.
В табл.11 показано как нужно соединять логические элементы И-НЕ для реализации любых других основных логических функций. Эту таблицу запоминать не требуется, но она может оказаться полезной в работе с цифровыми электронными устройствами.
Таблица 11
Логические функции |
Условное обозначение |
Схема с использованием только логических элементов И-НЕ |
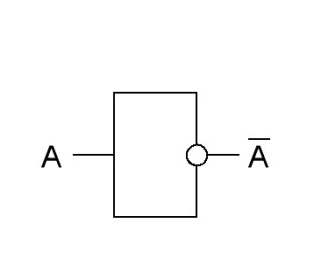
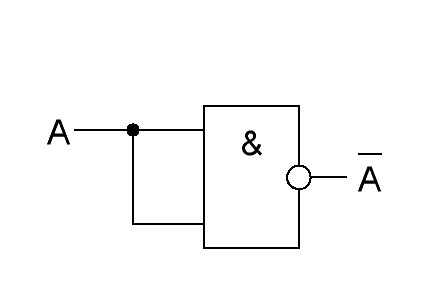
Инвертор |
|
|
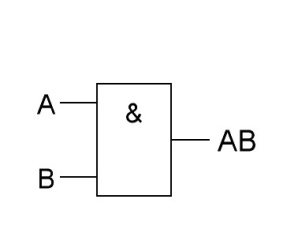
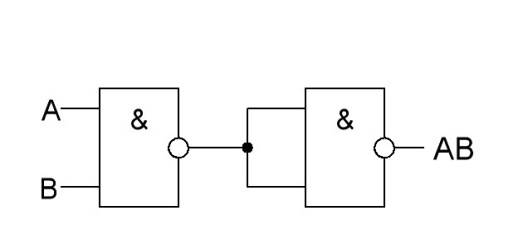
И |
|
|
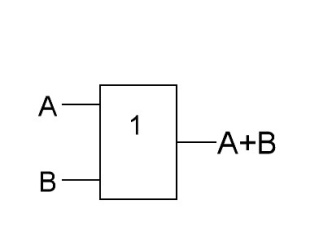
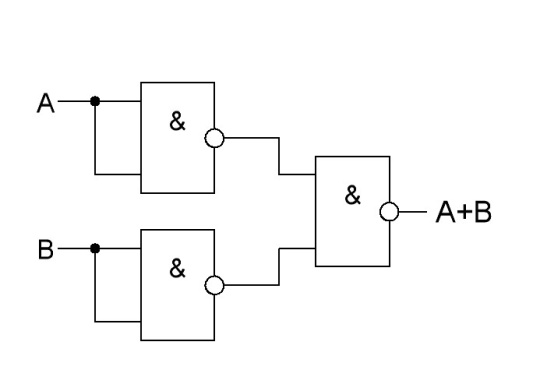
ИЛИ |
|
|
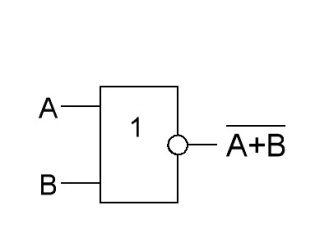
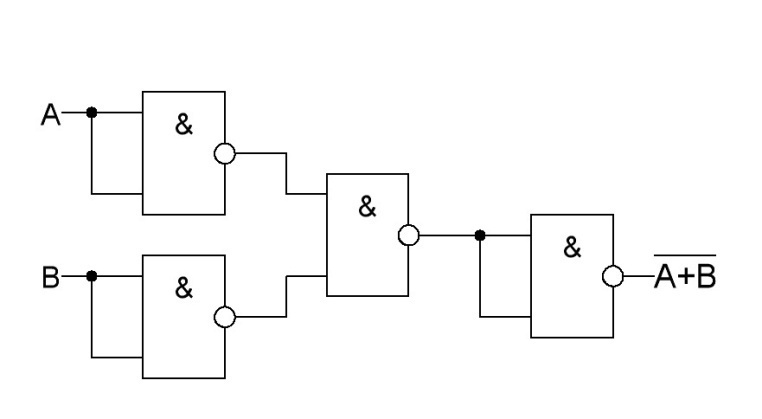
ИЛИ-НЕ |
|
|
ИЛИ ИСКЛЮЧАЮЩЕЕ |
|
|
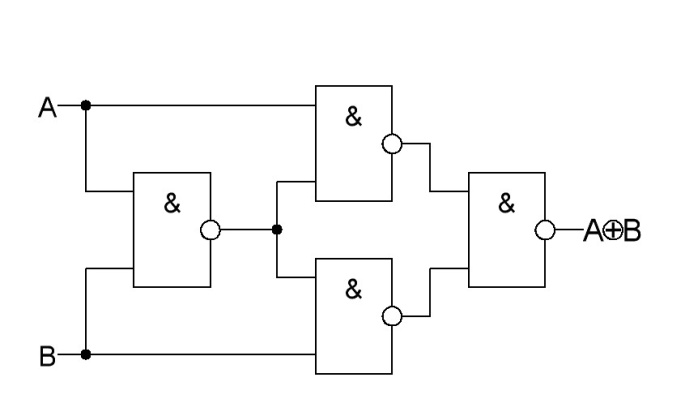
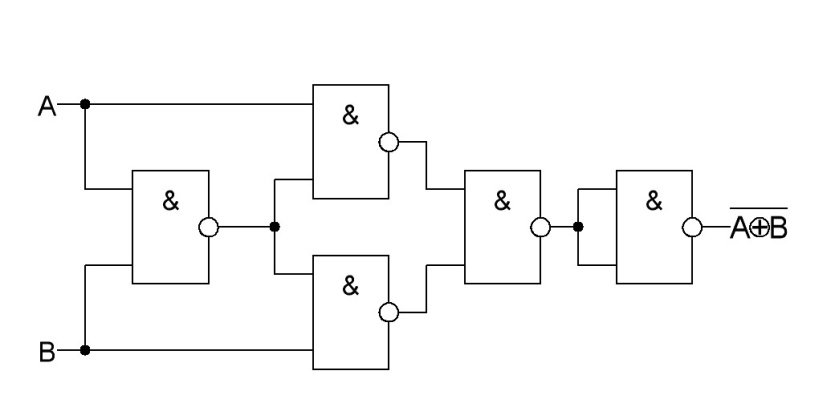
ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ |
|
|
Здесь необходимо отметить, что подобное преобразование возможно и для логического элемента ИЛИ-НЕ, взятого в качестве универсального. Это вытекает из известной теоремы Моргана, которое в алгебраической форме можно записать следующим образом:
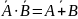
или
Прежде чем перейти к рассмотрению задач практического применения логических элементов, подведем краткий итог. Все устройства цифровой электроники строятся на основе четырех основных логических элементов. Это элементы: ИЛИ, И, ИЛИ ИСКЛЮЧАЮЩЕЕ и НЕ. Кроме того, дополнение этих элементов отрицанием выхода дает нам еще три универсальных логических элемента: ИЛИ-НЕ, И-НЕ и ИЛИ ИСКЛЮЧАЮЩЕЕ-НЕ. В табл.12 приведена сводная таблица базовых логических элементов.
Таблица 12
Логическая функция |
Условное обозначение |
Логическое выражение |
Таблица истинности |
||
1 |
2 |
3 |
4 |
||
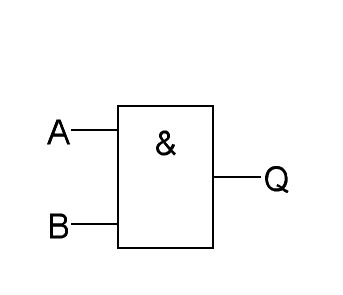
И |
|
A∙B=Q |
Входы |
Выход |
|
В |
А |
Q |
|||
0 |
0 |
0 |
|||
0 |
1 |
0 |
|||
1 |
0 |
0 |
|||
1 |
1 |
1 |
|||
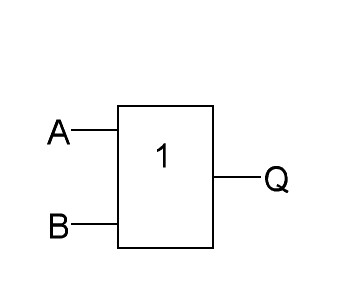
ИЛИ |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
|||
1 |
0 |
1 |
|||
1 |
1 |
1 |
|||
Инвертор (НЕ) |
|
|
|
0 |
1 |
|
1 |
0 |
|||
Продолжение табл.12
1 |
2 |
3 |
4 |
||
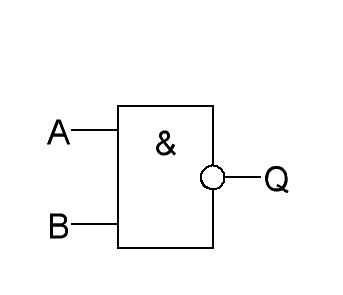
И-НЕ |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|||
1 |
0 |
1 |
|||
1 |
1 |
0 |
|||
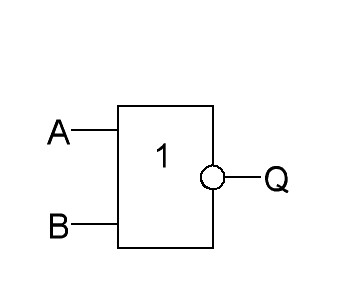
ИЛИ-НЕ |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
|||
1 |
0 |
0 |
|||
1 |
1 |
0 |
|||
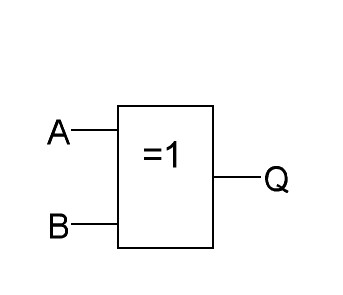
ИЛИ ИСКЛЮЧАЮЩЕЕ |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
|||
1 |
0 |
1 |
|||
1 |
1 |
0 |
|||
ИЛИ ИСКЛЮЧАЮЩЕЕ -НЕ |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
|||
1 |
0 |
0 |
|||
1 |
1 |
1 |
|||
